論理ゲートは、デジタル エレクトロニクス エンジニアリングの最も重要な要素の 1 つです。これはブール関数の概念に基づいて動作します。デジタル エレクトロニクスにはいくつかのゲートがあります。NOR ゲートはそのうちの 1 つであり、特定の構成で NOR ゲートを接続することで、AND、OR、NOT ゲートなどの他の基本的な論理ゲートを実装するために使用できるため、ユニバーサル ゲートの下にもあります。
NOR ゲートは、2 つ以上のバイナリ入力と出力バイナリ信号の間で NOR 演算を実行するデジタル論理ゲートです。 ORゲートとNOTゲートを組み合わせたものです。
NORゲートとは何ですか?
論理ゲート 2つ以上の入力の出力を決定する小型のデジタルスイッチング回路です。 ブール関数 バイナリ形式で。論理 1 は True または High を意味し、論理 0 は False または Low を意味します。さまざまな論理演算に基づいて、出力は異なります。論理ゲートには多くの入力がありますが、出力は 1 つだけです。各論理ゲートには、入力と出力のすべての組み合わせを表す独自の真理値表があります。
NOR ゲートは、OR ゲートの反対または補数であるユニバーサル ゲートと見なされます。
NORゲートの動作
真理値表からの挙動によれば、
DFA オートマトンの例
1 を返します、 すべての入力が 0 の場合
0 を返します、 いずれかの入力が 1 であるか、すべての入力が 1 である場合。
ブール式 NOR ゲートの値は次のとおりです。
A と B を 2 つの入力、O を出力とみなした場合、2 入力 NOR ゲートの式は次のようになります。
O = (A + B)’
NORゲートのシンボル
NOR ゲートの論理記号を次の図に示します。この図では、変数 A と B は入力行を表し、( A + B)」 NOR ゲートの出力です。
NORゲートの真理値表
NOR ゲートの真理値表を以下に示します。この表は、NOR ゲートの入力と出力の関係を示しています。これは、さまざまな入力の組み合わせに対する NOR ゲートの動作に関する情報も提供します。
NOR ゲートの論理記号と真理値表
マージソートJava
NOR ゲートの種類
NOR ゲートには、入力の数に基づいて 2 つのタイプがあります。
- 2 – 入力 NOR ゲート
- 3 – 入力 NOR ゲート
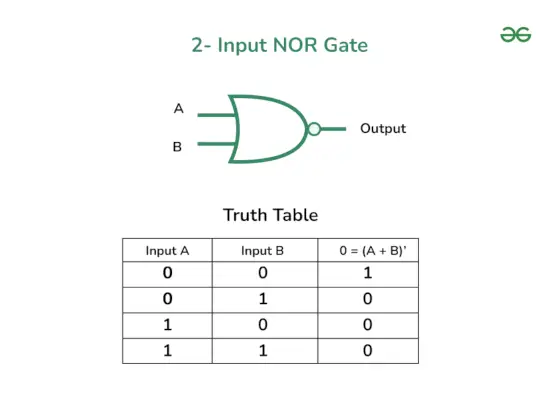
2 – 入力 NOR ゲート
これは最も単純な NOR ゲートの 1 つです。入力数 n = 2 なので、真理値表は 2 になります。n= 22= 4 つの組み合わせ。
以下は 2 入力 NOR ゲートの真理値表と論理図です。
2入力NORゲートの真理値表
2 入力 NOR ゲートの真理値表は上に示します。この表は、2 入力 NOR ゲートの入力と出力の関係を示しています。これは、さまざまな入力の組み合わせに対する 2 入力 NOR ゲートの動作に関する情報も提供します。
2入力NORゲートの論理図
2入力NORゲートの論理記号を上図に示します。この図では、変数 A と B は入力行を表し、( A + B)」 は 2 入力 NOR ゲートの出力です。
3 – 入力 NOR ゲート
名前自体からわかるように、入力は 3 つ必要なので、n = 3 になります。真理値表には 2 が含まれます。3= 考えられる結果の 8 つの組み合わせ。
以下は 3 入力 NOR ゲートの真理値表と論理図です。

htmlリストボックス
3入力NORゲートの真理値表
3 入力 NOR ゲートの真理値表は上に示します。この表は、3 入力 NOR ゲートの入力と出力の関係を示しています。これは、さまざまな入力の組み合わせに対する 3 入力 NOR ゲートの動作に関する情報も提供します。
3入力NORゲートの論理図
3入力NORゲートの論理記号を上図に示します。この図では、変数 A、B、C は入力行を表し、( A + B + C)」 3 入力 NOR ゲートの出力です。
トランジスタの観点から見た NOR ゲート
NOR ゲートはさまざまな方法でトランジスタを使用して実装できますが、次の 2 つの方法があります。 トランジスタ という方法が最も一般的な方法です。ここでは回路図の図と基本的な説明を示します。
トランジスタの観点から見た NOR ゲート
回路の働き
ここで、上の図には 2 つのトランジスタ T1 と T2 (この接合は NOR ゲートとして機能します) があり、これらは並列構成でグランドに接続されています。抵抗 A を T1 に接続し、抵抗 B を T2 に接続します。次に、T1 と T2 の接続点の間に抵抗を接続します。
手術
- 入力 A と B の両方が論理レベル 0 (GND) にある場合、トランジスタ T1 も T2 もオンになり、出力は抵抗 R を介して Vcc (論理 1) にプルアップされます。
- 入力 A または B (または両方) が論理レベル 1 (Vcc) にある場合、対応するトランジスタがオンになり、アクティブ化されたトランジスタを通じて出力が効果的に接地されます。これは出力をプルします 電圧 GND(論理0)まで下がります。
したがって、トランジスタ T2 のコレクタの出力は、入力 A と B の論理 NOR になります。
NORゲートの応用例
- インバーター機能: 単一入力 NOR ゲートは、インバータまたは ゲートではありません 。一方の入力が入力信号に接続され、もう一方の入力がグランド (0V) に接続されている場合、出力は入力の逆になります。
- メモリコンポーネント: NOR ゲートは、SR ラッチや D などの基本的なメモリ要素の作成に役立ちます。 ラッチ 、複雑なデジタル回路とメモリユニットの基本的な構成要素として機能します。
- ブール論理: NOR ゲートは、さまざまなブール論理関数を実装する際に重要な役割を果たします。さまざまな方法で組み合わせて作成できます。 そして 、OR、NOT ゲートであり、他のすべての論理演算の基礎を形成します。
- デコーダ: NOR ゲートはデコーダ回路に不可欠なコンポーネントであり、バイナリ情報を拡張形式に変換し、メモリのアドレス指定や出力選択などのタスクを容易にします。
- 演算回路: NOR ゲートは、2 進数に対して論理演算を実行する、加算器や減算器などの算術回路の設計における貴重な資産です。
- プログラマブル ロジック デバイス (PLD): NOR ゲートは頻繁に使用されます。 PLD カスタムロジック機能を実現し、デジタル回路設計における多用途の要素にします。
- クロック回路: NOR ゲートはデジタル システムのクロック生成および分配回路に貢献し、同期と正確なタイミング制御を保証します。
- エラー検出: リードソロモン符号などの特定の誤り検出符号では、NOR ゲートがパリティ チェックの計算とデータ送信時の誤りの修正に利用されます。
NORゲートのメリット
- 普遍: NOR ゲートは、さまざまな論理機能を実装できるユニバーサル ゲートとして機能します。
- シンプルさ: NOR ゲート回路は、単純な設計と理解しやすさを提供します。
- 低消費電力: 通常、NOR ゲートは他のゲート タイプよりも電力要件が低くなります。
- トラブルシューティングの容易さ: NOR ゲート回路は単純であるため、トラブルシューティングは簡単です。
- ノイズ耐性: NOR ゲートは優れたノイズ耐性を示し、信号干渉の影響を軽減します。
- 費用対効果: NOR ゲートは、電子アプリケーションでの製造と使用が経済的です。
NORゲートのデメリット
- 制限された機能: NOR ゲートは、すべての論理関数を単独で効率的に実装することができません。
- 特定のケースにおける複雑さ: 特定の論理関数に使用すると、代替ゲートと比較して複雑になる可能性があります。
- 応答時間が遅い: NOR ゲートは、特定のシナリオでより遅い伝播遅延を示す場合があります。
- 特殊な用途には不向き: 特定の特殊なアプリケーションでは、代替ゲートの方が適切な場合があります。
- 追加のコンポーネントが必要です: NOR ゲートとは異なるゲートを構築すると、追加のコンポーネントが必要となり、全体の複雑さが増す場合があります。
結論
この記事では、NOR ゲートについて学びました。 NOR ゲートはブール値を入力として受け取り、すべての入力が 0 の場合、入力のいずれかが 1 またはすべての入力が 1 の場合、「1」を返します。この記事では、真理値表、シンボリック表現、解決された例と、記事の理解を深めるのに役立つアプリケーション。
NOR ゲート – FAQ
NOR ゲートの実例を挙げてください。
Nor Gate は、メモリ回路、制御システム、通信デバイスなど、多くの電子デバイスでは使用できません。
NORゲートとORゲートの違いは何ですか?
NOR ゲートは OR ゲートの補数であり、その逆も同様です。
NORをインバータとして使用するにはどうすればよいですか?
NOR ゲートは、入力の一方をもう一方の入力に接続することでインバータとして使用できます。両方の入力が同じ場合、反対の出力が生成されます。
Javaのdoubleを文字列に変換する
ド・モルガンの定理とNORゲートの関係は何ですか?
ド・モルガンの定理は、OR 演算を NOR 演算に、またはその逆に変換する方法を示しています。
