- プッシュダウン オートマトンは、通常の文法用に DFA を設計するのと同じ方法で CFG を実装する方法です。 DFA は有限量の情報を記憶できますが、PDA は無限量の情報を記憶できます。
- プッシュダウン オートマトンは、単に「外部スタック メモリ」で強化された NFA です。スタックの追加は、プッシュダウン オートマトンに後入れ先出しのメモリ管理機能を提供するために使用されます。プッシュダウン オートマトンは、無制限の量の情報をスタックに保存できます。スタック上の限られた量の情報にアクセスできます。 PDA は、要素をスタックの最上部にプッシュしたり、要素をスタックの最上部からポップオフしたりできます。要素をスタックに読み取るには、先頭の要素をポップオフして失われる必要があります。
- PDA は FA よりも強力です。 FA で受け入れられる言語は、PDA でも受け入れられます。 PDA は、FA ですら受け入れられない言語のクラスも受け入れます。したがって、PDA は FA よりもはるかに優れています。
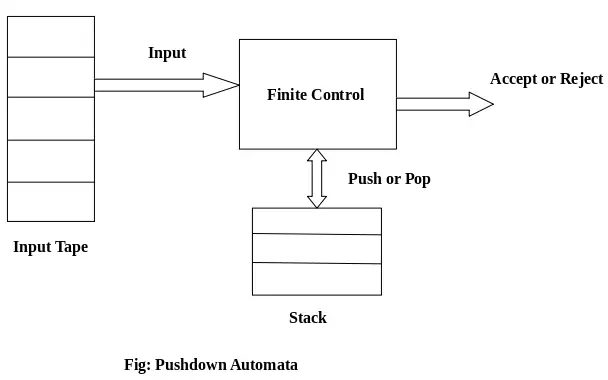
PDA コンポーネント:
入力テープ: 入力テープは多くのセルまたはシンボルに分割されています。入力ヘッドは読み取り専用で、一度に 1 シンボルずつ左から右にのみ移動できます。
有限制御: 有限コントロールには、読み取られる現在のシンボルを指すポインタがあります。
スタック: 書庫は片端からのみ押して取り出せる構造です。それは無限のサイズを持っています。 PDA では、スタックはアイテムを一時的に保管するために使用されます。
PDA の正式な定義:
PDA は、次の 7 つのコンポーネントの集合として定義できます。
質問: 状態の有限集合
∑: 入力セット
子: スタックからプッシュおよびポップできるスタック シンボル
q0: 初期状態
Javaで自動配線されるものは何ですか
と: Γ にある開始記号。
F: 最終状態のセット
d: 現在の状態から次の状態に移動するために使用されるマッピング関数。
瞬間的な説明 (ID)
ID は、PDA が入力文字列を計算し、その文字列が受け入れられるか拒否されるかを決定する方法を示す非公式の表記です。
瞬間的な記述はトリプル (q、w、α) であり、次のとおりです。
q 現在の状態を説明します。
で 残りの入力について説明します。
Linuxのエクスポートとは何ですか
ある 左上にスタックの内容を示します。
回転式改札口の表記:
⊢ 記号は改札口の表記を表し、1 つの手を表します。
⊢* 記号は一連の動きを表します。
例えば、
(p, b, T) ⊢ (q, w, α)
Cの関数
上記の例では、状態 p から q への遷移中に、入力シンボル 'b' が消費され、スタックの先頭 'T' が新しい文字列 α で表されます。
例 1:
言語を受け入れるための PDA を設計するnb2n。
解決: この言語では、n 個の a の後に 2n 個の b が続く必要があります。したがって、非常に単純なロジックを適用します。つまり、1 つの 'a' を読み取る場合、2 つの a をスタックにプッシュします。 「b」を読み取るとすぐに、単一の「b」ごとに 1 つの「a」だけがスタックからポップされます。
ID は次のように構築できます。
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa)
b を読み取ると、状態を q0 から q1 に変更し、対応する 'a' のポップを開始します。したがって、
δ(q0, b, a) = (q1, ε)
したがって、すべてのシンボルが読み取られない限り、「b」をポップするこのプロセスが繰り返されます。ポッピング動作は状態 q1 でのみ発生することに注意してください。
δ(q1, b, a) = (q1, ε)
すべての b を読み取った後、対応するすべての a がポップされるはずです。したがって、入力シンボルとして ε を読み取るとき、スタックには何も存在しないはずです。したがって、移動は次のようになります。
δ(q1, ε, Z) = (q2, ε)
どこ
PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})
ID は次のように要約できます。
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε)
ここで、入力文字列「aaabbbbbb」に対してこの PDA をシミュレートします。
δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT
例 2:
言語を受け入れるための PDA を設計する 0n1メートル0n。
解決: この PDA では、n 個の 0 の後に任意の数の 1 が続き、さらに n 個の 0 が続きます。したがって、このような PDA の設計ロジックは次のようになります。
最初の 0 が見つかったら、すべての 0 をスタックにプッシュします。 1 を読んだ場合は、何もしません。次に 0 を読み取り、0 を読み取るたびにスタックから 0 を 1 つポップします。
文字列ビルダー
例えば:

このシナリオは ID 形式で次のように記述できます。
δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state)
ここで、入力文字列「0011100」に対してこの PDA をシミュレートします。
δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT
