この記事では、データ構造におけるツリーの走査について説明します。 「ツリー トラバーサル」という用語は、ツリーの各ノードを横断または訪問することを意味します。リンク リスト、キュー、スタックなどの線形データ構造をトラバースする方法は 1 つあります。一方、ツリーを横断するには次のような複数の方法があります。

• 事前注文トラバーサル
• インオーダートラバーサル
• 郵便注文のトラバース

したがって、この記事では、ツリーをトラバースする上記のテクニックについて説明します。それでは、ツリートラバーサルの方法について説明しましょう。

事前注文トラバーサル

この手法は、「root left right」ポリシーに従います。これは、最初にルート ノードが訪問され、その後、左のサブツリーが再帰的に走査され、最後に右のサブツリーが再帰的に走査されることを意味します。ルート ノードは左右のサブツリーの前 (または前) にトラバースされるため、事前順序トラバーサルと呼ばれます。

したがって、事前順序トラバーサルでは、各ノードはその両方のサブツリーの前にアクセスされます。

事前注文トラバーサルのアプリケーションには以下が含まれます:

• ツリーのコピーを作成するために使用されます。
• 式ツリーのプレフィックス式を取得するために使用することもできます。

アルゴリズム

 Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively. 

例

次に、プリオーダー トラバーサル手法の例を見てみましょう。

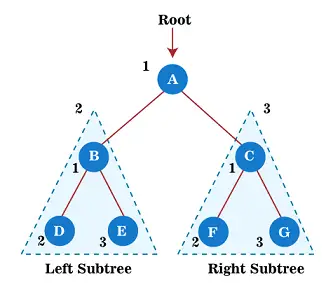
ここで、上記のツリーに事前順序トラバーサルの適用を開始します。まず、ルートノードをたどります A; その後、その左側のサブツリーに移動します B 、これも予約注文で横断されます。

したがって、左側のサブツリー B については、まずルート ノード B それ自体を横断します。その後、その左側のサブツリー D 横断されます。以来ノード D 子がありません。右のサブツリーに移動します そして 。ノード E にも子がないため、ルート ノード A の左側のサブツリーの走査が完了します。

ラテックスマトリックス

ここで、ルート ノード A の右のサブツリー、つまり C に向かって移動します。したがって、右のサブツリー C では、最初にルート ノードが C それ自体を横断しました。その後、その左側のサブツリー F 横断されます。以来ノード F 子がない場合は、右のサブツリーに移動します G 。ノード G にも子がないため、ルート ノード A の右側のサブツリーの走査が完了します。

したがって、ツリーのすべてのノードが走査されます。したがって、上記のツリーの事前順序トラバーサルの出力は次のようになります。

文字列に含まれる

A→B→D→E→C→F→G

データ構造における事前注文トラバーサルの詳細については、次のリンクを参照してください。 事前注文トラバーサル 。

郵便注文のトラバース

この手法は、「左右ルート」ポリシーに従います。これは、ルート ノードの最初の左側のサブツリーが走査され、その後、右側のサブツリーが再帰的に走査され、最後にルート ノードが走査されることを意味します。ルート ノードは左右のサブツリーの後で (または後置で) トラバースされるため、ポストオーダー トラバーサルと呼ばれます。

したがって、ポストオーダー トラバーサルでは、各ノードはその両方のサブツリーの後にアクセスされます。

ポストオーダートラバーサルのアプリケーションには以下が含まれます:

• ツリーを削除するために使用されます。
• 式ツリーの後置式を取得するためにも使用できます。

アルゴリズム

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node. 

例

次に、ポストオーダー トラバーサル手法の例を見てみましょう。

ここで、上記のツリーにポストオーダー トラバーサルの適用を開始します。まず、事後順序で走査される左側のサブツリー B を走査します。その後、右のサブツリーをたどります C ポストオーダーで。そして最後に、上記のツリーのルート ノード、つまり、 あ 、を横断します。

したがって、左サブツリー B については、まずその左サブツリー D 横断されます。以来ノード D 子がありません。正しいサブツリーをトラバースします。 そして 。ノード E にも子がないため、ルート ノードに移動します。 B. ノードを通過した後 B、 ルート ノード A の左側のサブツリーの走査が完了します。

ここで、ルート ノード A の右側のサブツリー (C) に向かって移動します。つまり、右側のサブツリー C については、まず左側のサブツリーを作成します。 F 横断されます。以来ノード F 子がありません。正しいサブツリーをトラバースします。 G 。ノード G にも子がないため、最終的には、右のサブツリーのルート ノード、つまり、 C、 横断されます。ルート ノード A の右側のサブツリーの走査が完了しました。

会社と会社の違い

最後に、指定されたツリーのルート ノードをたどります。つまり、 あ 。ルート ノードをトラバースした後、指定されたツリーのポストオーダー トラバースが完了します。

したがって、ツリーのすべてのノードが走査されます。したがって、上記のツリーの事後探索の出力は次のようになります。

D→E→B→F→G→C→A

データ構造におけるポストオーダートラバーサルの詳細については、次のリンクを参照してください。 郵便注文のトラバース 。

インオーダートラバーサル

この手法は、「左ルート右」ポリシーに従います。これは、ルート ノードをトラバースした後、最初に左のサブツリーにアクセスし、最後に右のサブツリーをトラバースすることを意味します。ルート ノードは左右のサブツリー間を走査するため、順序走査と呼ばれます。

したがって、順序トラバーサルでは、各ノードはそのサブツリーの間で訪問されます。

インオーダートラバーサルのアプリケーションには以下が含まれます:

• BST ノードを昇順で取得するために使用されます。
• 式ツリーのプレフィックス式を取得するために使用することもできます。

アルゴリズム

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively. 

例

java ハズネクスト

ここで、Inorder traversal 手法の例を見てみましょう。

ここで、上記のツリーに順序トラバーサルの適用を開始します。まず、左側のサブツリーをトラバースします。 B それは順番に走査されます。その後、ルートノードをたどります あ 。そして最後に、右のサブツリー C 順番に巡回されます。

したがって、左側のサブツリーについては、 B 、最初にその左側のサブツリー D 横断されます。以来ノード D には子がないため、それを走査した後、ノード B トラバースされ、最後にノード B の右側のサブツリー、つまり そして 、を横断します。ノード E にも子はありません。したがって、ルート ノード A の左側のサブツリーの走査が完了します。

その後、指定されたツリーのルート ノードをトラバースします。つまり、 あ 。

最後に、ルート ノード A の右のサブツリー、つまり C に向かって移動します。まず、その左側のサブツリー F 横断されます。以来ノード F 子はありません、ノード C をたどって、最後にノード C の右側のサブツリー、つまり、 G 、を横断します。ノード G にも子はありません。したがって、ルート ノード A の右側のサブツリーの走査が完了します。

ツリーのすべてのノードが走査されると、指定されたツリーの順序走査が完了します。上記のツリーの順序トラバーサルの出力は次のとおりです -

D→B→E→A→F→C→G

データ構造における順序トラバーサルの詳細については、次のリンクを参照してください。 インオーダートラバーサル 。

ツリートラバーサル手法の複雑さ

上で説明したツリー トラバーサル手法の時間計算量は次のとおりです。 の上） 、 どこ 「ん」 二分木のサイズです。

CSSのセレクターとは何ですか

一方、上で説明したツリー トラバーサル手法の空間の複雑さは ○(1) 関数呼び出しのスタック サイズを考慮しない場合。それ以外の場合、これらの技術の空間の複雑さは次のようになります。 おお） 、 どこ 「は」 木の高さです。

ツリートラバーサルの実装

ここで、さまざまなプログラミング言語を使用した上記の手法の実装を見てみましょう。

プログラム： C でツリー トラバーサル手法を実装するプログラムを作成します。

 #include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
 The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
 The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
 The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } 

出力

プログラム： C# でツリー トラバーサル手法を実装するプログラムを作成します。

 using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } 

出力

プログラム： C++ でツリー トラバーサル手法を実装するプログラムを作成します。

 #include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node-&gt;element = val; Node-&gt;left = NULL; Node-&gt;right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout&lt;<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root-&gt;left); cout&lt;<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root-&gt;right); cout&lt;<' '<element<left="createNode(28);" root->right = createNode(48); root-&gt;left-&gt;left = createNode(23); root-&gt;left-&gt;right = createNode(33); root-&gt;left-&gt;left-&gt;left = createNode(13); root-&gt;left-&gt;left-&gt;right = createNode(26); root-&gt;right-&gt;left = createNode(43); root-&gt;right-&gt;right = createNode(58); root-&gt;right-&gt;right-&gt;left = createNode(53); root-&gt;right-&gt;right-&gt;right = createNode(68); cout&lt;<'
 the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
 inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + &apos; &apos;); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + &apos; &apos;); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + &apos; &apos;); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println(&apos;The Preorder traversal of given binary tree is - &apos;); pt.traversePreorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Inorder traversal of given binary tree is - &apos;); pt.traverseInorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Postorder traversal of given binary tree is - &apos;); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that&apos;s all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'>

出力

上記のコードを実行すると、出力は次のようになります -

結論

この記事では、さまざまな種類のツリー トラバーサル手法 (事前順序トラバーサル、インオーダー トラバーサル、ポストオーダー トラバーサル) について説明しました。これらの手法を、C、C++、C#、および Java でのアルゴリズム、例、複雑さ、および実装とともに見てきました。

それでは、この記事については以上です。参考になれば幸いです。