Python プログラミングにおける Set は、反復可能で変更可能で、重複する要素を持たない順序付けされていないコレクション データ型です。
セットは { } (中括弧で囲まれた値) で表されます。
セットを使用することの主な利点は、 リスト は、特定の要素がセットに含まれているかどうかを確認するための高度に最適化されたメソッドを備えていることです。これは、ハッシュ テーブルとして知られるデータ構造に基づいています。セットには順序がないため、リストのようにインデックスを使用して項目にアクセスすることはできません。
Python セットの例
Python3
var>=> {>'Geeks'>,>'for'>,>'Geeks'>}> type>(var)> |
>
>
出力:
set>
時間計算量: O(1)
補助スペース: O(1)
Python Set メソッドを使用した型キャスト
Python set() メソッドは型キャストに使用されます。
Python3
# typecasting list to set> myset>=> set>([>'a'>,>'b'>,>'c'>])> print>(myset)> # Adding element to the set> myset.add(>'d'>)> print>(myset)> |
>
>
出力:
Python セットは順序付けされていないデータ型です。つまり、セットの要素がどの順序で格納されるかを知ることができません。
{'c', 'b', 'a'} {'d', 'c', 'b', 'a'}> 時間計算量: O(n)
補助スペース: O(n)
Python Setで一意性と不変性をチェックする
Python セットは重複した値を持つことができず、一度作成された値は変更できません。
Python3
# Python program to demonstrate that> # a set cannot have duplicate values> # and we cannot change its items> # a set cannot have duplicate values> myset>=> {>'Geeks'>,>'for'>,>'Geeks'>}> print>(myset)> # values of a set cannot be changed> myset[>1>]>=> 'Hello'> print>(myset)> |
>
>
出力:
最初のコードは、セットに重複した値を含めることができないことを説明しています。その中のすべてのアイテムはユニークな価値があります。
2 番目のコードは、セットの作成後に値を割り当てたり変更したりできないため、エラーを生成します。セット内の項目の追加または削除のみが可能です。
{'Geeks', 'for'} TypeError: 'set' object does not support item assignment> Python セットを使用した異種要素
Python セットは異種要素を格納できます。つまり、セットには文字列、整数、ブール値などのデータ型を組み合わせて格納できます。
Python3
# Python example demonstrate that a set> # can store heterogeneous elements> myset>=> {>'Geeks'>,>'for'>,>10>,>52.7>,>True>}> print>(myset)> |
>
>
出力:
{True, 10, 'Geeks', 52.7, 'for'}> 時間計算量: O(n)
補助スペース: O(n)
Python の凍結セット
冷凍セット Python の は、適用先の固定セットに影響を与えずに結果を生成するメソッドと演算子のみをサポートする不変オブジェクトです。 Pythonのfrozenset()メソッドで実現できます。
セットの要素はいつでも変更できますが、フリーズされたセットの要素は作成後も同じままです。
パラメータが渡されない場合は、空のフローズンセットが返されます。
パイソン
# Python program to demonstrate differences> # between normal and frozen set> # Same as {'a', 'b','c'}> normal_set>=> set>([>'a'>,>'b'>,>'c'>])> print>(>'Normal Set'>)> print>(normal_set)> # A frozen set> frozen_set>=> frozenset>([>'e'>,>'f'>,>'g'>])> print>(>'
Frozen Set'>)> print>(frozen_set)> # Uncommenting below line would cause error as> # we are trying to add element to a frozen set> # frozen_set.add('h')> |
>
>
出力:
Normal Set {'a', 'c', 'b'} Frozen Set {'e', 'g', 'f'}> 時間計算量: O(n)
補助スペース: O(n)
Set の内部動作
これは、ハッシュ テーブルとして知られるデータ構造に基づいています。同じインデックス位置に複数の値が存在する場合、値はそのインデックス位置に追加され、リンクされたリストが形成されます。
Python セットでは、ダミー変数を含むディクショナリを使用して実装されます。ここで、キーは、時間計算量を大幅に最適化したメンバー セットです。
セットの実装:
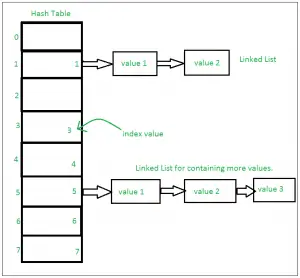
単一の HashTable に対する多数の操作を含むセット:
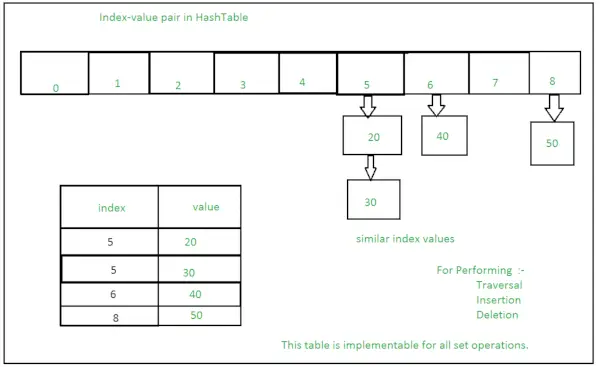
セットのメソッド
Python セットへの要素の追加
セットへの挿入は、 set.add( ) 関数。適切なレコード値が作成され、ハッシュ テーブルに保存されます。項目をチェックするのと同じです。つまり、平均 O(1) です。ただし、最悪の場合、次のような事態になる可能性があります。 の上) 。
Python3
# A Python program to> # demonstrate adding elements> # in a set> # Creating a Set> people>=> {>'Jay'>,>'Idrish'>,>'Archi'>}> print>(>'People:'>, end>=> ' '>)> print>(people)> # This will add Daxit> # in the set> people.add(>'Daxit'>)> # Adding elements to the> # set using iterator> for> i>in> range>(>1>,>6>):> >people.add(i)> print>(>'
Set after adding element:'>, end>=> ' '>)> print>(people)> |
>
>
出力:
People: {'Idrish', 'Archi', 'Jay'} Set after adding element: {1, 2, 3, 4, 5, 'Idrish', 'Archi', 'Jay', 'Daxit'}> 時間計算量: O(n)
補助スペース: O(n)
Python セットのユニオン演算
Union() 関数または | を使用して 2 つのセットをマージできます。オペレーター。両方のハッシュ テーブル値にアクセスし、マージ操作を実行して要素を結合し、同時に重複を削除します。これの時間計算量は次のとおりです。 O(len(s1) + len(s2)) ここで、s1 と s2 は結合を行う必要がある 2 つのセットです。
Python3
# Python Program to> # demonstrate union of> # two sets> people>=> {>'Jay'>,>'Idrish'>,>'Archil'>}> vampires>=> {>'Karan'>,>'Arjun'>}> dracula>=> {>'Deepanshu'>,>'Raju'>}> # Union using union()> # function> population>=> people.union(vampires)> print>(>'Union using union() function'>)> print>(population)> # Union using '|'> # operator> population>=> people|dracula> print>(>'
Union using '|' operator'>)> print>(population)> |
>
>
出力:
Union using union() function {'Karan', 'Idrish', 'Jay', 'Arjun', 'Archil'} Union using '|' operator {'Deepanshu', 'Idrish', 'Jay', 'Raju', 'Archil'}> 時間計算量: O(n)
補助スペース: O(n)
Python セットの交差演算
これは、intersection() または & 演算子を通じて実行できます。共通要素が選択されています。これらは、ハッシュ リストの反復と、両方のテーブルの同じ値の結合に似ています。この時間計算量は O(min(len(s1), len(s2)) です。ここで、s1 と s2 は結合を行う必要がある 2 つのセットです。
Python3
# Python program to> # demonstrate intersection> # of two sets> set1>=> set>()> set2>=> set>()> for> i>in> range>(>5>):> >set1.add(i)> for> i>in> range>(>3>,>9>):> >set2.add(i)> # Intersection using> # intersection() function> set3>=> set1.intersection(set2)> print>(>'Intersection using intersection() function'>)> print>(set3)> # Intersection using> # '&' operator> set3>=> set1 & set2> print>(>'
Intersection using '&' operator'>)> print>(set3)> |
>
>
出力:
Intersection using intersection() function {3, 4} Intersection using '&' operator {3, 4}> 時間計算量: O(n)
補助スペース: O(n)
Python でセットの違いを見つける
セット間の違いを見つけるため。リンクされたリスト内の相違点を見つけるのと似ています。これは、difference() または – 演算子によって行われます。差分 s1 – s2 を求める時間計算量は O(len(s1))
Python3
# Python program to> # demonstrate difference> # of two sets> set1>=> set>()> set2>=> set>()> for> i>in> range>(>5>):> >set1.add(i)> for> i>in> range>(>3>,>9>):> >set2.add(i)> # Difference of two sets> # using difference() function> set3>=> set1.difference(set2)> print>(>' Difference of two sets using difference() function'>)> print>(set3)> # Difference of two sets> # using '-' operator> set3>=> set1>-> set2> print>(>'
Difference of two sets using '-' operator'>)> print>(set3)> |
>
プログラミングパターンJava
>
出力:
Difference of two sets using difference() function {0, 1, 2} Difference of two sets using '-' operator {0, 1, 2}> 時間計算量: O(n)
補助スペース: O(n)
Python セットのクリア
Set Clear() メソッドは、セット全体をその場で空にします。
Python3
# Python program to> # demonstrate clearing> # of set> set1>=> {>1>,>2>,>3>,>4>,>5>,>6>}> print>(>'Initial set'>)> print>(set1)> # This method will remove> # all the elements of the set> set1.clear()> print>(>'
Set after using clear() function'>)> print>(set1)> |
>
>
出力:
Initial set {1, 2, 3, 4, 5, 6} Set after using clear() function set()> 時間計算量: O(n)
補助スペース: O(n)
ただし、Python セットには 2 つの大きな落とし穴があります。
- セットは要素を特定の順序で維持しません。
- 不変型のインスタンスのみを Python セットに追加できます。
セットの時間計算量
| 手術 | 平均的なケース | 最悪の場合 | ノート |
|---|---|---|---|
| sのx | ○(1) | の上) | |
| ユニオン s|t | O(レン(s)+レン(t)) | ||
| 交差点(&T) | O(min(len(s), len(t)) | O(レン(s) * レン(t)) | t がセットでない場合は、最小値を最大値に置き換えます |
| 複数の交差点 s1&s2&..&sn | (n-1)*O(l) ここで、l は max(len(s1),...,len(sn)) | ||
| 差 s-t | O(のみ) |
集合の演算子
セットとフリーズ セットは次の演算子をサポートします。
| オペレーター | ノート |
|---|---|
| 「s」を入力してください | 封じ込めチェック |
| キーが s にありません | 非含有チェック |
| s1 == s2 | s1 は s2 と同等です |
| s1 != s2 | s1 は s2 と同等ではありません |
| s1 <= s2 | s1 は s2 のサブセットです |
| s1 | s1 は s2 の適切なサブセットです |
| s1>= s2 | s1 は s2 のスーパーセットです |
| s1> s2 | s1 は s2 の適切なスーパーセットです |
| s1 | s2 | s1 と s2 の結合 |
| s1 & s2 | s1 と s2 の交点 |
| s1 – s2 | s1 にはあるが s2 には含まれていない要素のセット |
| s1 ^ s2 | s1 または s2 のいずれかにある要素のセット |
Python セットに関する最近の記事。
