あ スタック は、操作が実行される特定の順序に従う線形データ構造です。順序は次のとおりかもしれません LIFO(後入れ先出し) または FILO(先入れ後出し) 。 LIFO これは、最後に挿入された要素が最初に出力され、 行 これは、最初に挿入された要素が最後に出力されることを意味します。

目次

• さまざまな言語でのスタックの実装
• スタックデータ構造とは何ですか?

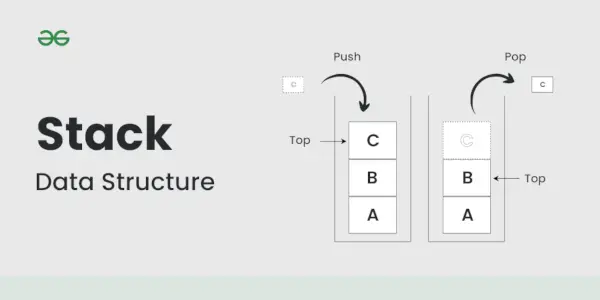
  スタックは、次の線形データ構造です。 後入れ先出し (LIFO) 原理。これはプレートのスタックのように動作し、最後に追加されたプレートが最初に削除されます。

  次のように考えてください。

  • 要素をスタックにプッシュすることは、上に新しいプレートを追加することに似ています。
  • 要素をポップすると、スタックから上部プレートが削除されます。

  ポップ : スタックから最上位の要素を削除します。

• ピーク : 先頭の要素を削除せずに返します。
• 空です : スタックが空かどうかを確認します。
• 一杯 : スタックがいっぱいかどうかを確認します (固定サイズ配列の場合)。

• C++ STL でのスタック
• Javaのスタッククラス
• Python でスタックする
• C# でスタックする
• JavaScriptでのスタックの実装

配列内に 2 つのスタックを実装する

キューを使用したスタックの実装

単一の配列に k 個のスタックを効率的に実装するにはどうすればよいでしょうか?

O(1) 時間で O(1) の追加スペースで getMin() をサポートするスタックを設計する

単一のキューを使用してスタックを実装する

優先キューまたはヒープを使用してスタックを実装するにはどうすればよいですか?

Deque を使用したスタックとキューの実装

接頭語から中置語への変換

接頭辞から接尾辞への変換

後置から前置への変換

後置から中置へ

中置記法を前置記法に変換する

式内のバランスの取れた括弧をチェックする

算術式の評価

後置式の評価

再帰を使用してスタックを反転する

個々の単語を反転する

スタックを使用して文字列を反転する

キューを逆転する

ストックスパン問題

次に優れた要素

次に大きい周波数要素

左右の次に大きいインデックスの最大積

反復的なハノイの塔

一時スタックを使用してスタックをソートする

O(n) で余分なスペースを使用せずにスタックを反転します

スタックの中間要素を削除する

スタックを使用してキューを別のキューにソートできるかどうかを確認する

配列がスタックソート可能かどうかを確認する

反復ポストオーダートラバーサル |セット 1 (2 つのスタックを使用)

ヒストグラム内の最大の長方形領域 |セット2

指定された配列内の各ウィンドウ サイズの最大値と最小値を検索します。

式内の指定された左括弧の右括弧のインデックスを検索します。

最も近い左右の小さい要素間の最大差を見つける

シーケンス内の連続した同じ単語を削除する

n分木でミラーをチェックする

スタックを使用して数値を反転する

キューの最初の K 要素を反転する

次に大きい数の Q クエリを出力します

反復ポストオーダートラバーサル |セット 2 (1 つのスタックを使用)

指定されたバイナリ ツリー ノードの祖先を再帰なしで出力します。

最長の有効な部分文字列の長さ

式に冗長な括弧が含まれているかどうか

式に重複した括弧が含まれているかどうかを調べる

配列内の次の小さい方と次の大きい方を検索します

特定のバイナリ ツリーの祖先を見つける反復手法

スタックの置換 (配列が他の配列のスタックの置換であるかどうかを確認します)

スパゲッティスタック

+ 演算子と – 演算子を含む代数文字列から括弧を削除します

最長の正しい括弧サブシーケンスの範囲クエリ

クイックリンク ：

• スタック上の「ビデオ」
• スタック上の「クイズ」

推奨：

• データ構造とアルゴリズムを学ぶ | DSA チュートリアル
• Scala でのスタック