摩擦は相対運動に抵抗する力であり、物体間の界面で発生しますが、流体の場合のように物体内部でも発生します。摩擦係数の概念は、レオナルド・ダ・ヴィンチによって初めて定式化されました。摩擦係数の大きさは、表面の性質、環境、表面の特徴、潤滑剤の有無などによって決まります。
摩擦の法則
摩擦の法則は 5 つあり、次のとおりです。
• 移動する物体の摩擦は垂直抗力に比例し、垂直になります。
• 物体が受ける摩擦は、物体が接触する表面の性質によって異なります。
• 接触面積がある限り、摩擦は接触面積に依存しません。
• 動摩擦は速度とは無関係です。
・静摩擦係数は動摩擦係数より大きい。
私たちが物体を見ると、その表面は滑らかに見えますが、同じ物体を顕微鏡で見ると、滑らかに見える物体にも粗いエッジがあることがわかります。小さな山や溝は顕微鏡で見ることができ、表面の凹凸として知られています。そのため、一方の物体を他方の物体の上に移動させると、表面上のこれらの凹凸が絡み合い、摩擦が生じます。粗さが大きいほど凹凸が大きくなり、加わる力も大きくなります。
静止摩擦
静摩擦の原因についてはいくつかの理論があり、ほとんどの摩擦関連の概念と同様に、それぞれの理論はある条件下では有効であることが証明されていますが、他の状況では無効になります。実世界のアプリケーション (特に産業機械やモーションに関連するアプリケーション)。静摩擦の背後にある 2 つの最も広く受け入れられている理論の制御は、表面の微細な粗さに関係しています。
表面がどれほど完璧に機械加工され、仕上げられ、洗浄されているかに関係なく、表面には必然的に凹凸が生じます。これは本質的に山脈のように山と谷からなる粗さです。 (技術的には、頂点は凹凸です。) 2 つの表面が接触している場合、それらの接触面積は大きく明確に定義されているように見えますが、実際には接触は特定の場所、つまり表面の凹凸が存在する場所でのみ発生します。両方の面が干渉します。
凹凸間のこれらの小さな接触面積の合計は、実際の接触面積または有効接触面積と呼ばれます。これらの個々の接触面積は非常に小さいため、これらの点での表面間の圧力 (圧力 = 力 ÷ 面積) は非常に高くなります。この極度の圧力により、分子レベルで発生する冷間圧接として知られるプロセスを介して、表面間に接着が発生します。表面が相互に移動する前に、この接着の原因となっている結合を破壊する必要があります。
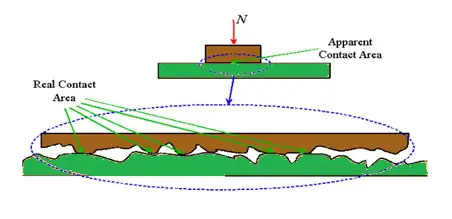
さらに、表面の粗さは、ある場所では一方の表面の凹凸がもう一方の表面の谷にはまり込むこと、つまり表面がかみ合うことを意味します。
これらの連動領域は、表面が移動する前に破壊または塑性変形する必要があります。言い換えれば、摩耗が発生する必要があります。したがって、ほとんどのアプリケーションでは、接触面の付着と摩耗の両方によって静摩擦が発生します。
静摩擦の法則
静摩擦には 2 つの法則があります。
- 第一法則: 静止摩擦力の最大値は接触面積に依存しません。
- 第二法則: 静止摩擦力の最大値は垂直抗力に匹敵します。つまり、垂直抗力が増加すると、物体が動かずに耐えることができる最大外力も増加します。

静摩擦の公式の導出
図に示すように、水平面上にある重量 mg のブロックを考えてみましょう。物体が表面に押し付けられると、たとえ表面が硬いように見えても、表面は変形します。変形した表面は、表面に垂直な垂直抗力 R でボディを押します。これを垂直反力といいます。それはmgのバランスをとります。
R = mg
ここで、ブロックに力 P が加わった場合を考えます。明らかに、物体は静止したままです。これは、他の力 F が水平方向に作用し、加えられた力 P に対抗して物体にかかる正味の力がゼロになるためです。このテーブル面と接触している物体の表面に沿って働く力Fを摩擦力といいます。
したがって、物体が動かない限り、F = P。これは、P を増加させると、摩擦 F も増加し、常に P に等しいことを意味します。
実際の動作が開始されるまでに作用するこの摩擦力は、静止摩擦として知られています。
静摩擦係数
静摩擦とは、物体を表面に置いたときに発生する摩擦です。そして、動摩擦は表面上の物体の動きによるものです。摩擦は摩擦係数によってよく特徴づけられ、摩擦力と垂直抗力の比として説明されます。これにより、オブジェクトが表面上に配置されやすくなります。静摩擦係数はスカラー量であり、μ で表されます。s。
静止摩擦係数の式は次のように表されます。
mu_{s} = frac{F}{N} どこ
メートル s = 静摩擦係数
F = 静摩擦力
N = 垂直抗力

動摩擦
動摩擦は、移動する表面間に作用する力として定義されます。表面上を移動する物体は、その移動の反対方向に力を受けます。力の大きさは、2 つの材料間の動摩擦係数によって異なります。
摩擦は、スライドする物体を押しとどめる力として簡単に定義できます。動摩擦はあらゆるものの一部であり、2 つ以上の物体の動きを妨げます。力は物体が滑ろうとする方向とは逆の方向に働きます。
車が停止しなければならない場合、私たちはブレーキをかけますが、そこにまさに摩擦が発生します。歩いていて、急に立ち止まりたくなったとき、また摩擦に感謝します。しかし、水たまりの真ん中で停止しなければならない場合、摩擦が少なく、あまり助けられないため、事態はさらに困難になります。

2 つの表面間の静摩擦を克服すると、基本的に、動きに対する分子的障害 (凹凸間の冷間圧接) と、ある程度の機械的障害 (表面の凹凸と谷の間の干渉) の両方が除去されます。動きが開始されると、ある程度の摩耗は発生し続けますが、静止摩擦中よりもはるかに低いレベルであり、表面間の相対速度により、追加の冷間圧接が発生するのに十分な時間がありません (極度に低い速度の場合を除く)。
付着と磨耗のほとんどが克服されて動きを誘発するため、表面間の動きに対する抵抗が減少し、表面は静摩擦よりもはるかに低い動摩擦の影響下で動くようになります。
動摩擦の法則
動摩擦には 4 つの法則があります。
- 第一法則: 動摩擦力 (Fk) は、接触している 2 つの表面間の通常の反応 (N) に正比例します。どこ、 メートル k = 動摩擦係数と呼ばれる定数。
- 第二法則: 動摩擦力は、接触する表面の形状や見かけの面積には依存しません。
- 第三法則: それは接触する表面の性質と材質によって異なります。
- 第 4 法則: 物体と表面の間の相対速度が大きすぎない限り、接触している物体の速度には依存しません。

動摩擦の公式
動摩擦係数はギリシャ文字のμ( メートル )、下付き文字 k が付きます。動摩擦力は、 メートル k 物体にかかる通常の力の倍になります。ニュートン(N)で表されます。
動摩擦方程式は次のように記述できます。
動摩擦力=(動摩擦係数)(垂直抗力)
F k = m k h
どこ、
F k = 動摩擦力
メートル k 動摩擦係数
h = 垂直抗力 (ギリシャ文字イータ)

動摩擦の公式の導出
重りのブロックを考えてみましょう mg 図のように水平面に置きます。物体が表面に押し付けられると、たとえ表面が硬いように見えても、表面は変形します。変形した表面が通常の力で本体を押す R それは表面に対して垂直です。これを垂直反力といいます。それはmgのバランスをとることです R = mg 。
例外処理Java
さて、それが力であると考えてみましょう P 図のようにブロックに適用されます。明らかに、体は他の力のために静止したままです F 水平方向に作用し、加えられた力に対抗します P その結果、ボディにかかる正味の力はゼロになります。テーブルの表面に接触している物体の表面に沿って作用するこの力 F は次のように呼ばれます。 摩擦力 。
体が動かない限り F = P 。これは、P を増加すると、摩擦 F も増加し、常に P に等しくなることを意味します。
加える力を摩擦の限界をわずかに超えて増やすと、実際の動きが始まります。これは摩擦がなくなったという意味ではありません。それは、力が限界摩擦を克服したことを意味するだけです。この段階での摩擦力は、動摩擦または動摩擦として知られています。
動摩擦または動摩擦は、物体が実際に別の物体の表面上を移動するときに作用する反対の力です。
静摩擦と動摩擦の応用

静摩擦の応用
静止摩擦の実例を以下に示します。
- 机の上の書類
- ラックに掛けられたタオル
- 本のしおり
- 丘の上に駐車した車
動摩擦の応用
動摩擦の実例を以下にいくつか示します。
- 摩擦は、2 つの物体をこするときなど、日常的な出来事でも大きな役割を果たします。その結果生じる動きは熱に変換され、場合によっては火災を引き起こします。
- また、磨耗の原因にもなるため、機械部品の潤滑には摩擦を軽減するオイルが必要です。
- 二つの物体がこすれると摩擦力が熱エネルギーに変換され、まれに火災が発生することがあります。
- 動摩擦は機械部品の摩耗の原因となるため、機械部品を油で潤滑することが重要です。
静摩擦と動摩擦の違い
| 静止摩擦 | 動摩擦 |
| 静摩擦は、互いに動かない 2 つ以上の物体の間に存在する摩擦です。 | 動摩擦は、相互に運動している 2 つ以上の物体の間に存在する摩擦です。 |
| 静止摩擦の大きさは、その係数の値が大きいほど大きくなります。 | 動摩擦係数の値が低いため、動摩擦の大きさは比較的小さくなります。 |
静止摩擦を表す式は次のように与えられます。 Fs= msh | 動摩擦を表す式は次のように与えられます。 Fk= mkh |
| その値はゼロにすることもできます。 | その値がゼロになることはありません。 |
| 例 - テーブルの上に鉛筆。 | 例 - テーブルの上で鉛筆を移動します。 |
静摩擦と動摩擦に基づくサンプル問題
質問 1: 男性が質量 75.0 kg の大きな段ボール箱を床に押します。
解決:
動摩擦係数はμですk= 0.520
作業者は前方に 400.0 N の力を加えます。
摩擦力の大きさはどれくらいでしょうか?
答え: 平面上では、物体の垂直抗力は次の式で求められます。
h = mg
η の値を式 F に代入すると、k= mkη 、わかります
Fk= (0.520) (75.0kg) (9.80m/s2) = 382.2N
質問 2: 上記の質問で、ボックスを動かす正味の力を計算しますか?
解決:
物体に作用する正味の力は、物体に作用するすべての力の合計です。
この場合、物体に作用する力は、人が加える力とその逆方向に働く動摩擦です。
前進運動が正であるとみなされる場合、正味の力は次のように計算されます。
Fネット= Fワーカー–Fk
上の式に値を代入すると、次のようになります。
Fネット= 400 N – 382.2 N = 17.8 N
質問 3: 回転運動で摩擦が生じるのはなぜですか?
答え:
理論的には、ボールは表面と点接触します。
しかし実際には、ボール(および/または表面)は荷重により変形し、接触面積は楕円形になります。
理論的には、ほとんどの回転軸受やリニア軸受 (すべり軸受を除く) に見られるような転がり面には摩擦力がかからないはずです。
しかし、実際のアプリケーションでは、転動面に摩擦が生じる要因が 3 つあります。
1. 表面間のマイクロスリップ (表面が互いにスライドします)
2. 材料の非弾性特性 (つまり、変形)
3. 表面の粗さ
質問 4: 質量 10 kg の物体が滑らかな表面に置かれています。これら 2 つの表面間の静摩擦は 15 N として与えられます。静摩擦係数を求めますか?
解決:
与えられた
m = 10kg
F=15N
メートルs= ?
私達はことを知っています、
垂直抗力、N = mg
したがって、N = 10× 9.81 = 98.1 N
静止摩擦係数の公式は次のとおりです。
メートルs= 15/N
ローカル日付Javaメートルs= 15/98.1
メートル s = 0.153
質問 5: 物体の垂直抗力と静摩擦力はそれぞれ 50 N と 80 N です。静摩擦係数を求めますか?
解決:
与えられた
N = 50N
F = 80 Nおよびμs= ?
静止摩擦係数の公式は次のとおりです。
メートルs= F/N
メートルs= 80/50
メートルs= 1.6
質問 6: 静摩擦と動摩擦の関係は何ですか?
答え:
静摩擦力は、静止した物体を静止させます。静摩擦力が克服されると、動摩擦力が移動する物体の速度を低下させます。
質問 7: 冷蔵庫の重さは 1619 N、静摩擦係数は 0.50 です。冷蔵庫を動かすのに最小の力はどれくらいですか?
解決:
与えられたデータ:
冷蔵庫の重量、W=1619 N
W=1619N
静摩擦係数、μs= 0.50
冷蔵庫を動かすのに必要な最小の力は次のように与えられます。
F = メートルsで
F = 0.50 × 1619
F = 809.50 N.
