強結合コンポーネント (SCC) は、グラフ理論とアルゴリズムの基本的な概念です。有向グラフでは、 強く接続されたコンポーネント は頂点のサブセットであり、サブセット内のすべての頂点は、有向エッジをトラバースすることによって、同じサブセット内の他のすべての頂点から到達可能です。を見つける SCC グラフの構造と接続性についての重要な洞察を提供し、次のようなさまざまな分野で応用できます。 ソーシャル ネットワーク分析、Web クローリング、ネットワーク ルーティング 。このチュートリアルでは、グラフ データ構造内の強接続コンポーネントを識別するための定義、プロパティ、および効率的なアルゴリズムについて説明します。
Javaメソッドの配列
目次
- 強接続コンポーネント (SCC) とは何ですか?
- 強接続コンポーネント (SCC) が重要な理由
- 接続コンポーネントと強接続コンポーネント (SCC) の違い
- 従来の DFS 手法を使用して強結合成分を検出できないのはなぜですか?
- 2 つの強く接続されたコンポーネントを一方向エッジで接続する
- 強く接続されたコンポーネントを見つけるための総当りアプローチ
- 強接続コンポーネント (SCC) を見つけるための効率的なアプローチ
- 結論
強接続コンポーネント (SCC) とは何ですか?
あ 強く結合した成分 有向グラフの は、頂点のすべてのペアが相互に到達可能な最大の部分グラフです。これは、このサブグラフ内の任意の 2 つのノード A および B には、A から B へのパスと B から A へのパスが存在することを意味します。
例えば: 以下のグラフには、同じ強連結成分内に各頂点から他のすべての頂点へのパスがあるため、2 つの強連結成分 {1,2,3,4} と {5,6,7} があります。

強く接続されたコンポーネント
強接続コンポーネント (SCC) が重要な理由
SCC を理解することは、次のようなさまざまなアプリケーションにとって重要です。
- ネットワーク分析 : 密接に相互接続されたノードのクラスターを識別します。
- Web クローラーの最適化 : 密接にリンクされている Web グラフの部分を決定します。
- 依存関係の解決 : ソフトウェアにおいて、どのモジュールが相互依存しているかを理解します。
接続コンポーネントと強接続コンポーネントの違い ( SCC)
での接続性 無向グラフ 2 つの頂点が相互に到達可能かどうかを指します。 2 つの頂点間にパスがある場合、それらの頂点は接続されていると言われます。その間 強くつながっている にのみ適用されます 有向グラフ 。有向グラフのサブグラフは、 強く接続されたコンポーネント (SCC) すべての頂点のペアに対して、かつその場合に限り あ そして B 、からのパスが存在します。 あ に B そしてからの道 B に あ 。その理由を見てみましょう 接続されているコンポーネントを見つけるための標準の dfs メソッド グラフ内の を使用して、強接続成分を決定することはできません。
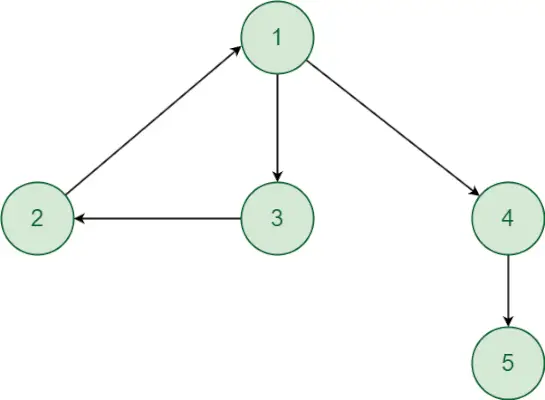
次のグラフを考えてみましょう。
Cでポインタを逆参照する方法さあ、始めましょう DFS 他の頂点にアクセスするには、頂点 1 から呼び出します。
なぜ従来の DFS 手法では強結合成分を見つけることができないのでしょうか?
すべての頂点には頂点 1 から到達できます。ただし、頂点 5、6、または 7 から頂点 1 への有向パスがないため、頂点 1 と 5、6、7 を同じ強く接続されたコンポーネント内に置くことはできません。グラフには 2 つの強接続コンポーネントがあります。連結成分 {1,2,3,4} と {5,6,7}。したがって、従来の dfs 法を使用して強連結成分を見つけることはできません。
2 つの強く接続されたコンポーネントを一方向エッジで接続する
あるコンポーネントの頂点と他のコンポーネントの頂点の間にエッジが追加されると、2 つの異なる接続されたコンポーネントが 1 つのコンポーネントになります。ただし、強く接続されたコンポーネントの場合はそうではありません。 1 つの SCC から他の SCC への一方向のエッジのみがある場合、2 つの強接続コンポーネントは 1 つの強接続コンポーネントにはなりません。
Base64 JavaScriptをデコードする

強く接続されたコンポーネントを見つけるための総当りアプローチ
簡単な方法は、各頂点 i (強コンポーネントの一部ではない) について、頂点 i を含む強接続コンポーネントの一部となる頂点を見つけることです。 2 つの頂点 i と j は、頂点 i から頂点 j へ、またはその逆の有向パスが存在する場合、同じ強接続コンポーネント内にあります。
次の例を使用してアプローチを理解しましょう。
- 頂点 1 から開始します。頂点 1 から頂点 2 へ、またはその逆のパスがあります。同様に、頂点 1 から頂点 3 へ、およびその逆のパスがあります。したがって、頂点 2 と 3 は、頂点 1 と同じ強接続コンポーネント内にあります。頂点 1 から頂点 4 および頂点 5 への有向パスはありますが、頂点 4,5 から頂点 1 への有向パスはないため、頂点 4および 5 は、頂点 1 と同じ強連結コンポーネント内にはありません。したがって、頂点 1、2、および 3 は強連結コンポーネントを形成します。
- 頂点 2 と頂点 3 については、強連結成分がすでに決定されています。
- 頂点 4 の場合、頂点 4 から頂点 5 へのパスはありますが、頂点 5 から頂点 4 へのパスはありません。したがって、頂点 4 と 5 は同じ強接続コンポーネントには存在しません。したがって、頂点 4 と頂点 5 は両方とも、単一の強く接続されたコンポーネントの一部になります。
- したがって、3 つの強接続コンポーネント {1,2,3}、{4}、および {5} が存在します。
上記のアプローチの実装を以下に示します。
C++ #include using namespace std; class GFG { public: // dfs Function to reach destination bool dfs(int curr, int des, vector>& 形容詞、ベクトル & vis) { // curr ノードが宛先の場合 return true if (curr == des) { return true; vis[curr] = 1; for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true; false を返します。 } // ソースから宛先へのパスが存在するかどうかを判断する // bool isPath(int src, int des, Vector>& 形容詞) { ベクトル vis(adj.size() + 1, 0); 戻り dfs(src, des, adj, vis); } // グラフの強く接続されたすべてのコンポーネントを // 返す関数。 ベクター> findSCC(int n, ベクトル>& a) { // 強く接続されたコンポーネントをすべて保存します。 ベクター> 答え; // 頂点が強連結成分ベクトルの一部であるかどうかを格納します。 // is_scc(n + 1, 0); ベクター> adj(n + 1); for (int i = 0; i< a.size(); i++) { adj[a[i][0]].push_back(a[i][1]); } // Traversing all the vertices for (int i = 1; i <= n; i++) { if (!is_scc[i]) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // thr part of thidl ist. vector scc; scc.push_back(i); for (int j = i + 1; j<= n; j++) { // If there is a path from vertex i to // vertex j and vice versa put vertex j // into the current SCC list. if (!is_scc[j] && isPath(i, j, adj) && isPath(j, i, adj)) { is_scc[j] = 1; scc.push_back(j); } } // Insert the SCC containing vertex i into // the final list. ans.push_back(scc); } } return ans; } }; // Driver Code Starts int main() { GFG obj; int V = 5; vector> エッジ{ { 1, 3 }、{ 1, 4 }、{ 2, 1 }、{ 3, 2 }、{ 4, 5 } }; ベクター> ans = obj.findSCC(V, エッジ); コート<< 'Strongly Connected Components are:
'; for (auto x : ans) { for (auto y : x) { cout << y << ' '; } cout << '
'; } }> ジャワ import java.util.ArrayList; import java.util.List; class GFG { // dfs Function to reach destination boolean dfs(int curr, int des, List> 形容詞、リスト vis) { // curr ノードが宛先の場合 return true if (curr == des) { return true; vis.set(curr, 1); for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true; false を返します。 } // ソースから宛先へのパスが存在するかどうかを判断する // boolean isPath(int src, int des, List> adj) { リスト vis = 新しい ArrayList(adj.size() + 1); for (int i = 0; i<= adj.size(); i++) { vis.add(0); } return dfs(src, des, adj, vis); } // Function to return all the strongly connected // component of a graph. List> findSCC(int n, リスト> a) { // 強く接続されたすべてのコンポーネントを保存します。 リスト> ans = 新しい ArrayList(); // 頂点が強接続コンポーネント リストの一部であるかどうかを格納します。 // is_scc = 新しい ArrayList(n + 1); for (int i = 0; i<= n; i++) { is_scc.add(0); } List> adj = 新しい ArrayList(); for (int i = 0; i<= n; i++) { adj.add(new ArrayList()); } for (List エッジ : a) { adj.get(edge.get(0)).add(edge.get(1)); } // すべての頂点を走査します (int i = 1; i<= n; i++) { if (is_scc.get(i) == 0) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // the part of this list. List scc = 新しい ArrayList(); scc.add(i); for (int j = i + 1; j<= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (is_scc.get(j) == 0 && isPath(i, j, adj) && isPath(j, i, adj)) { is_scc.set(j, 1); scc.add(j); } } // Insert the SCC containing vertex i into // the final list. ans.add(scc); } } return ans; } } public class Main { public static void main(String[] args) { GFG obj = new GFG(); int V = 5; List> エッジ = 新しい ArrayList(); edges.add(new ArrayList(List.of(1, 3))); edges.add(new ArrayList(List.of(1, 4))); edges.add(new ArrayList(List.of(2, 1))); edges.add(new ArrayList(List.of(3, 2))); edges.add(new ArrayList(List.of(4, 5))); リスト> ans = obj.findSCC(V, エッジ); System.out.println('強く接続されているコンポーネントは次のとおりです:'); for (リスト x : ans) { for (int y : x) { System.out.print(y + ' '); System.out.println(); } } } // このコードは shivamgupta310570 によって提供されました>>'パイソン
C# using System; using System.Collections.Generic; class GFG { // dfs Function to reach destination public bool Dfs(int curr, int des, List> 形容詞、リスト vis) { // curr ノードが宛先の場合、true を返します if (curr == des) { return true; vis[curr] = 1; foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true; false を返します。 } // ソースから宛先へのパスが存在するかどうかを判断する public bool IsPath(int src, int des, List> adj) { var show = 新しいリスト (adj.カウント + 1); for (int i = 0; i< adj.Count + 1; i++) { vis.Add(0); } return Dfs(src, des, adj, vis); } // Function to return all the strongly connected components of a graph public List> FindSCC(int n, リスト> a) { // 強結合コンポーネントをすべて保存します var ans = new List>(); // 頂点が強接続コンポーネントの一部であるかどうかを格納します var isScc = new List (n + 1); for (int i = 0; i< n + 1; i++) { isScc.Add(0); } var adj = new List>(n + 1); for (int i = 0; i< n + 1; i++) { adj.Add(new List ()); } for (int i = 0; i< a.Count; i++) { adj[a[i][0]].Add(a[i][1]); } // Traversing all the vertices for (int i = 1; i <= n; i++) { if (isScc[i] == 0) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // the part of this list. var scc = new List (); scc.Add(i); for (int j = i + 1; j<= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj)) { isScc[j] = 1; scc.Add(j); } } // Insert the SCC containing vertex i into // the final list. ans.Add(scc); } } return ans; } } // Driver Code Starts class Program { static void Main(string[] args) { GFG obj = new GFG(); int V = 5; List> エッジ = 新しいリスト> { 新しいリスト { 1, 3 }、新しいリスト { 1, 4 }、新しいリスト { 2, 1 }、新しいリスト { 3, 2 }、新しいリスト { 4, 5 } }; リスト> ans = obj.FindSCC(V, エッジ); Console.WriteLine('強く接続されているコンポーネントは次のとおりです:'); foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' '); Console.WriteLine(); } } } // このコードは shivamgupta310570 によって提供されました>>'JavaScript
出力
Strongly Connected Components are: 1 2 3 4 5>
時間計算量: O(n * (n + m))、 頂点のペアごとに、それらの間にパスが存在するかどうかをチェックしているためです。
補助スペース:O(N)
Pythonのeol
強接続コンポーネント (SCC) を見つけるための効率的なアプローチ
グラフ内の SCC を見つけるには、次のようなアルゴリズムを使用できます。 コサラジュのアルゴリズム または Tarjan のアルゴリズム 。これらのアルゴリズムを段階的に見てみましょう。
1. コサラジュのアルゴリズム :
Kosaraju のアルゴリズムには、次の 2 つの主要なフェーズが含まれます。
- 元のグラフに対する深さ優先検索 (DFS) の実行 :
- まず元のグラフに対して DFS を実行し、ノードの終了時間 (つまり、DFS がノードの探索を完全に終了した時間) を記録します。
- 転置グラフでの DFS の実行 :
- 次に、グラフ内のすべてのエッジの方向を反転して、転置されたグラフを作成します。
- 次に、最初のフェーズで記録された終了時間の降順にノードを考慮して、転置されたグラフに対して DFS を実行します。
- このフェーズの DFS トラバーサルごとに 1 つの SCC が与えられます。
以下は、Kosaraju のアルゴリズムの簡略版です。
- 元のグラフ上の DFS : 終了時間を記録します。
- グラフを転置する : すべてのエッジを反転します。
- 転置グラフ上の DFS : 終了時間が短い順にノードを処理して SCC を見つけます。
2. Tarjan のアルゴリズム :
Tarjan のアルゴリズムは、スタックと追加のブックキーピングを使用して単一の DFS パスで SCC を検出するため、より効率的です。
- DFS トラバーサル : DFS 中に、各ノードのインデックスと、ノードから到達できる最小のインデックス (ローリンク値) を維持します。
- スタック : 現在再帰スタック (探索されている現在の SCC の一部) 内にあるノードを追跡します。
- SCC の特定 : ノードのローリンク値がそのインデックスと等しい場合、それは SCC が見つかったことを意味します。現在のノードに到達するまで、スタックからすべてのノードをポップします。
Tarjan のアルゴリズムの簡単な概要は次のとおりです。
- 初期化する
index>0にします。 - 未訪問のノードごとに DFS を実行します。
- ノードのインデックスとローリンク値を設定します。
- ノードをスタックにプッシュします。
- 隣接ノードごとに、アクセスされていない場合は DFS を実行し、スタック内にある場合はローリンク値を更新します。
- ノードのローリンク値がそのインデックスと等しい場合、スタックからノードをポップして SCC を形成します。
結論
理解と発見 強く接続されたコンポーネント 有向グラフの使用は、コンピューター サイエンスの多くのアプリケーションにとって不可欠です。 コサラジュさん そして タルジャンさんの アルゴリズムは SCC を識別する効率的な方法であり、それぞれに独自のアプローチと利点があります。これらの概念をマスターすることで、複雑なネットワークの構造と動作をより適切に分析し、最適化することができます。