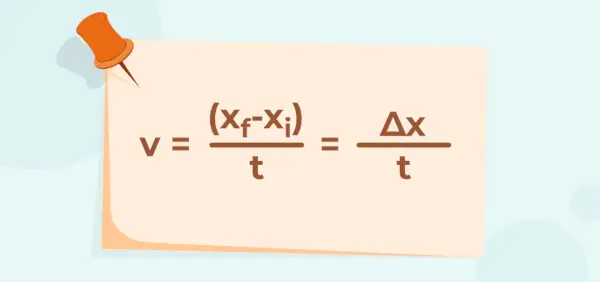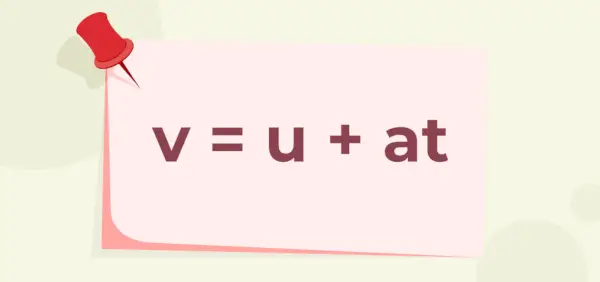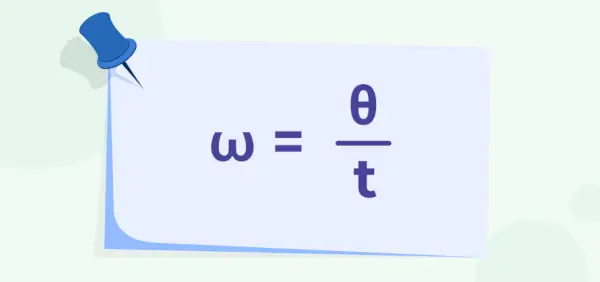速度 は物理学において重要な概念であり、時間に対する物体の位置の変化率を測定します。物体の速度が特定の方向で測定される場合、それは速度と呼ばれます。また、変位の時間変化は速度として知られています。速度と速度は互いに非常に似ています。しかし、速度は大きさと方向の両方を持つベクトル量であるという点で重要な違いを示します。そして速度は大きさだけを持つスカラー量です。したがって、速度は、物体が方向のある目的地に到達するのにどれくらいの時間がかかるかの尺度です。
目次
Javaのスタックとは何ですか
たとえば、2 つの物体が同じ方向に移動している場合、どちらが速いかを判断するのが簡単です。ただし、2 つのオブジェクトの運動方向が逆の場合、最も速いオブジェクトを特定することは困難です。このような状況では、速度の概念が不可欠です。
速度の定義
速度は、基準フレームおよび時間に対するオブジェクトの位置の変化率として定義されます。

速度 は、移動の速度と方向のベクトル尺度です。簡単に言えば、速度は何かが特定の方向に移動する速度です。主要高速道路を北に向かう車の速度も、宇宙に飛び出すロケットの速度も、どちらも速度を使用して測定される可能性があります。ご想像のとおり、ベクトル速度のスカラー サイズ (合計値) が移動の速度を表します。計算の観点から言えば、速度は時間の観点からその場所から最初に抜けることです。速度は、測定値、距離、時間を使用する簡単な式で計算できます。
速度の単位
- 速度の SI 単位は次のとおりです。 MS (メートル/秒)。
- 同時に、速度は任意の距離単位で表すことができます。他の単位には、マイル/時 (mph)、キロメートル/時 (kph)、およびキロメートル/秒 (km/s) があります。
速度の種類
どのオブジェクトにもさまざまなタイプの速度が存在します。これらのタイプのいくつかは次のとおりです。
- 均一速度
- 不均一な速度
- 瞬間速度
- 平均速度
これらの速度を次のように理解しましょう。
均一速度
物体が同じ時間に同じ変位を移動するとき、その速度は等速と呼ばれます。時速 80 キロメートル (km/h) の一定速度で 2 時間走行する列車は、160 キロメートル (km) の距離を移動します。時速 80 キロメートルで走行する列車の速度は等速度の一例です。
不均一な速度
物体が等時間間隔で不等変位を移動するとき、その速度は不等速度と呼ばれます。たとえば、混雑した道路を 30 km/h で走行し、高速道路で 80 km/h まで加速し、郊外で 50 km/h まで減速した場合、その車は問題を抱えていると言われます。 -均一速度。
瞬間速度
任意の物体の特定の瞬間または非常に短い期間における速度は、瞬間速度と呼ばれます。高速道路を時速 100 km の一定速度で走行する車を考えてみましょう。ドライバーが速度計を見てその速度を確認するのが、その瞬間の瞬間速度の一例です。
平均速度
ある程度の速度で移動する物体の場合、単位時間当たりに移動する合計距離は、その物体の平均速度と呼ばれます。つまり、
平均速度 = 総移動変位 / 総所要時間
人が 4 km の距離を 1 時間で歩き、さらに 2 km を 30 分で歩くと考えてみましょう。全行程の平均速度は時速 8 キロメートル (km/h) です。
初速と終速
初期速度 オブジェクトの動きが開始されたときの速度です。簡単に言うと、時間間隔 t = 0 s における速度を初速度と呼びます。それは記号uで表されます。 SI 単位は速度の単位、つまり m/s に似ています。
最終速度 物体が最大加速度に達したときに到達する速度です。簡単に言うと、一定の時間間隔でオブジェクトが獲得する速度を最終速度と呼びます。これは記号 v で表されます。初速と終速の SI 単位は同じ (m/s) です。
最終速度を求めるにはどうすればよいですか?
オブジェクトの最終速度を見つけるには、次の手順に従います。
ステップ1: オブジェクトの初速度は、総移動距離をオブジェクトがその距離を移動するのにかかった時間で割ることによって計算できます。式 V = d/t では、V は速度、d は距離、t は時間です。
ステップ2: 物体の質量を力で割り、その結果に加速度の時間を乗算することで、加速度を求めることができます。
ステップ 3: 最終的な速度を取得するには、ステップ 1 と 2 の量を加算します。
等速性
物体の等速性は、物体が一定方向に一定の速度を持つ場合に得られます。ここでは、一定の方向により、オブジェクトが直線または直線のパスで移動するように制限されます。したがって、等速度は、物体の直線運動を一定の速度で移動することと呼ばれます。
最も単純な運動形式の 1 つは、物体が一定の速度で移動する場合です。このような一定の動きは、物体が水平面上を滑るたびに観察できます。
しかし、円軌道を時速50kmの一定速度で走行する自転車は、速度は一定ですが、円軌道に沿って進行方向が変化するため、等速ではありません。
速度の計算式
さまざまな条件下でさまざまなパラメータを使用して物体の速度を計算するには、さまざまな式があります。以下に、さまざまな速度を計算するために使用される主な式をいくつか示します。
最初の (x私) と最終位置 (xf物体の速度と時間間隔が与えられると、速度は次のように計算できます。
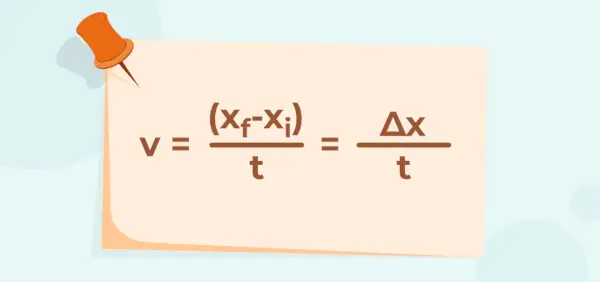
さて、運動方程式に従って速度を評価できます。
- 初速度、加速度、時間が与えられると、最終速度は次のように与えられます。
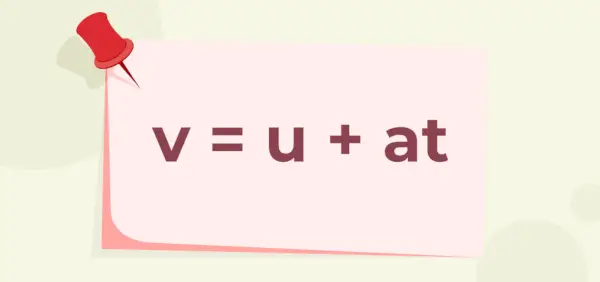
どこ
- で は最終速度、
- で は初速度、
- ある は加速度であり、
- t オブジェクトにかかった時間です。
速度と速度の違い
速度と速度はよく似た意味で使用される用語なので、ほとんどの人にとって少し混乱します。しかし、実際には、両方の用語の間には大きな違いがあります。
速度という用語は、物体の移動速度を表すために使用されます。ただし、速度は速度を表すだけでなく、物体の移動方向についても簡潔に示します。
したがって、 速度は、特定の時間間隔内に物体が移動した距離の変化率として単純に定義されます。一方、速度は、特定の時間間隔における物体の変位速度として定義されます。 これは、速度が距離の関数であり、速度が変位の関数であることを意味します。そして最も重要なことは、速度は大きさのみを持つと言われているため、スカラー量であるのに対し、速度は大きさと方向の両方を持ち、ベクトル量であるということです。さらに、どちらの量も同じ単位と寸法式を持ちます。
Speed と Velocity の違いを表形式で表すと、次のようになります。
| スピード | 速度 |
|---|---|
| 一定の時間内に物体が移動する距離の変化率を速度といいます。 | 速度は、特定の時間間隔における物体の変位速度として定義されています。 |
| それは距離のみの関数です。 | ただし、これは変位のみの関数です。 |
| 速度は大きさのみを持つと言われているため、スカラー量も存在します | 速度は大きさと方向の両方を持ちますが、ベクトル量です。 |
| 物体の移動速度が負になることはありません | 移動する物体の速度はゼロになる可能性があります。 |
| 速度は物体がどれだけ速く動くかを示します。 | 一方、速度は、オブジェクトが一方向にどれだけ速く移動するかを示します。 |
角速度
物体の円運動にかかる角変位と時間が与えられると、角速度は次のように与えられます。
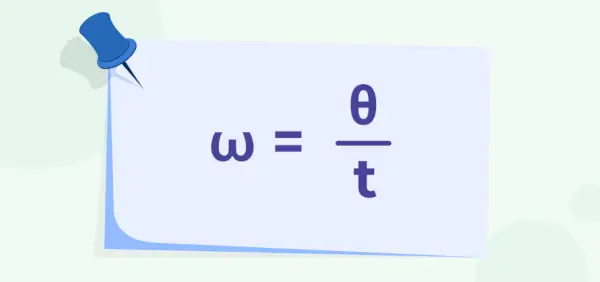
どこ、
- おお は角速度です
- 私 角変位メンです
- t 物体が円運動するのにかかった時間です。
脱出速度
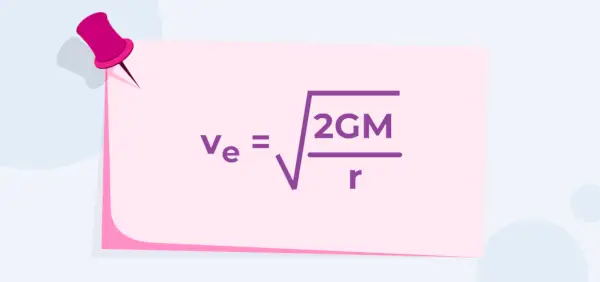
地球の重力 (重力定数 G) から逃れた物体の質量が与えられると、物体の脱出速度は次のように与えられます。
どこ、
- で それは は脱出速度、
- G は万有引力定数 (= 6.674 × 10-十一Nm2/kg2)、
- メートル は逃げた物体の質量であり、
- r は質量の中心からの距離です。
速度の公式のまとめ
さまざまな速度を計算するためのさまざまな式はすべて次のとおりです。
- v = s / t
- v = (x f - バツ 私 )/t = Δx / t
- v = u + で
- ω = θ / t
- で それは = √2Gm/r
また、チェックしてください
- 距離と変位
- 加速度
- 速度と速度
速度に関する解決例
例 1: 車は 1 時間で 550 km 移動します。その速度を計算します。
解決:
考えると、
Javaハッシュマップ
- 変位、s = 550 km = 550 × 103メートル
- 所要時間、t = 1 時間 = 3600 秒
以来、
速度 = 変位 / 時間
v = 550 × 103/3600
= 152.77 m/秒
したがって、車の速度は 152.77 m/s となります。
例 2: 車が発進し、10 秒間で 40 m の変位を移動します。その速度を計算します。
解決:
考えると、
- 初期位置、x私= 0m
- 最終位置、xf= 40メートル
- 所要時間、t = 10 秒。
以来、
C++ ペアv = xf- バツ私/t
したがって、
v = (40 m – 0 m) / 10 秒
= 4m/秒
したがって、車の速度は 4 m/s となります。
例 3: プレーヤーが最初は静止していたサッカーボールを打ち、20 ミリ秒の加速に達しました。 -2 時間的には5秒。 t = 5 秒後のサッカーの最終速度を決定します。
解決:
考えると、
- 加速度、a = 20ms-2
- 初速度、u = 0 m/s
- 所要時間、t = 5 秒。
以来、
v = u + で
したがって、
v = 0 m/s + 20 ミリ秒-2×5秒
= 100m/秒
したがって、t = 5 秒後のフットボールの最終速度は 100 m/s になります。
Javaでリストを反復する
例 4: 5 秒間に 30 ラジアンの角度だけ円運動で変位するボールの角速度を求めます。
解決:
考えると、
- 角変位、θ = 30 rad
- 所要時間、t = 5 秒
したがって、角速度は次のように与えられます。
ω = θ / t
したがって、
ω = 30 rad / 5 秒
= 6 ラジアン/秒
したがって、ボールの角速度は 6 rad/s です。
例 5: 最終速度 20 m/s、加速度 2 m/s で完走する人 2 4秒以内に。その初速度を計算します。
解決:
考えると、
- 加速度、a = 2ms-2
- 初速度、v = 20 m/s
- 所要時間、t = 4 秒。
したがって、初速度は次のようになります。
u = v – で
したがって、
u = 20 m/s – 2 ms-2×4秒
= 12m/秒
したがって、人の初速度は 12 m/s となります。
例 6: 地表からの物体の脱出速度はいくらになるでしょうか?
解決:
- 地球の質量、m = 6 × 1024kg、
- 質量の中心から物体までの距離は地球の半径に等しい、r = 6400 km = 6.4 × 106メートル、そして
- 重力定数の値 G = 6.67 × 10−11Nm2/kg2。
したがって、エスケープ速度は次のように定義されます。
でそれは= √2Gm/r
したがって、
でそれは= √2 × 6.67 × 10−11×6 ×1024kg/6.4×106メートル
= 11200m/秒
= 11.2 km/秒
ループ 1 ~ 10 の bashしたがって、物体の地表からの脱出速度は 11.2 km/s になります。
ベロシティ – よくある質問
速度を定義します。
物体の特定の方向の速度を測定するとき、それを速度といいます。たとえば、時速 40 km で北に向かって移動する車が速度の例です。
速度はどのように測定されますか?
速度は時間あたりの距離の単位で測定され、通常はメートル/秒 (m/s) またはキロメートル/時 (km/h) です。オブジェクトの速度とその移動方向の両方が必要です。
瞬間速度とは何ですか?
瞬間速度は、特定の瞬間における物体の速度として定義されます。 m/s 単位で測定されます。
速度の単位とは何ですか?
速度の SI 単位は m/s (メートル/秒) です。また、時速マイル (mph)、時速キロメートル (kph)、秒あたりのキロメートル (km/s) でも測定されます。
速度がゼロになることはありますか?
はい、速度がゼロになる可能性があります。静止している物体の速度は常に 0 です。
速度の種類は何ですか?
速度には主に平均速度と瞬間速度の 2 種類があります。平均速度は総変位をかかった総時間で割ったもので、瞬間速度は特定の瞬間における物体の速度です。
速度が負の値になることはありますか?
はい、速度は負の値になる可能性があります。
速度に影響を与える要因は何ですか?
速度に影響を与える可能性のある要因には、重力、摩擦、空気抵抗などの外力と、力のバランスが崩れている場合の物体の質量が含まれます。これらの要因のいずれかが変化すると加速が発生し、それによって速度が変化する可能性があります。
どのようにして速度が負になるのでしょうか?
反対方向のオブジェクトの速度は常に負の符号で考慮されます。
速度が一定の場合、加速度は ____ です。
等速運動の加速度は0m/sです2速度は変わらないので。
速度と速度はどう違うのですか?
速度と速度は両方とも何かがどれだけ速く動いているかを測定しますが、速度には動きの方向も含まれます。これにより速度はベクトル量になりますが、速度は動きの大きさのみを表すスカラー量になります。
速度はベクトル量ですか?
はい、速度はベクトル量です。
なぜ速度がベクトル量なのか?
物体の速度を定義するには、方向だけでなく大きさも必要であるため、速度はベクトル量です。
平均速度の計算式とは何ですか?
平均速度の公式は次のように与えられます。
平均速度 = 総移動変位 / 総所要時間
速度と速度の違いは何ですか?
特定の方向に測定された速度は速度と呼ばれます。つまり、車が時速 30 km で移動している場合は車の速度ですが、車が北に向かって時速 30 km で移動している場合は車の速度になります。