の XOR または排他的 OR ゲート デジタル電子機器で排他的 OR 演算を実行するために使用される特殊なタイプの論理ゲートです。 XOR ゲートは 2 つの入力を受け取り、適用された 2 つの入力の組み合わせに応じて出力を生成します。
この記事では、完全な説明をします XOR ゲートの理論 それと一緒に 真理値表 、 ブール式 、 論理記号 、 回路図 、 もっと。
目次
XORゲートとは何ですか?
で デジタルエレクトロニクス 、2 つの入力を受け取り、入力の組み合わせに対して実行された排他的論理和演算の結果である出力を生成する XOR ゲートと呼ばれる論理回路があります。この論理ゲートは、両方の入力が異なる場合に High または論理 1 出力を生成し、そうでない場合は論理 0 出力を生成します。
XORゲートの動作
XOR ゲートの動作は次のように説明できます。
1 を返します、 論理ハイ入力の数が奇数の場合。
javaからjsonオブジェクトへ0 を返します、 論理 High 入力の数が偶数の場合。
A と B という 2 つの入力があり、出力が X であるとすると、式は次のようになります。
XOR ゲートのブール式は次のとおりです。
文字列をJavaの整数に変換
X = A'B + AB'
XORゲートのシンボル
XOR ゲートの論理記号を次の図に示します。この図では、変数 A と B は入力行を表し、 A'B + AB' XOR ゲートの出力です。
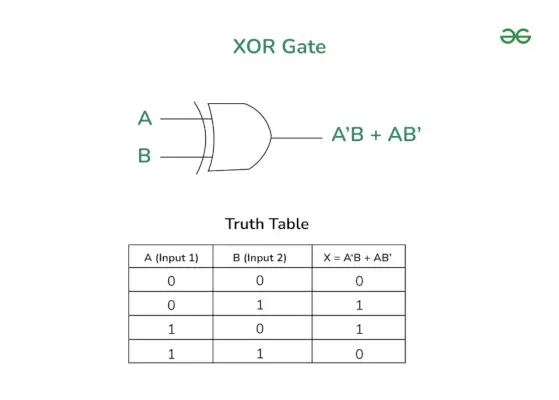
XOR ゲートの論理記号と真理値表
XORゲートの真理値表
XOR ゲートの真理値表を以下に示します。この表は、XOR ゲートの入力と出力の関係を示しています。これは、さまざまな入力の組み合わせに対する XOR ゲートの動作に関する情報も提供します。
3 本以上の入力ラインを備えた単一の XOR ゲートがないことに注意することが重要です。 2 入力 XOR ゲートのみが存在します。ただし、3 つ以上の入力ラインを持つ XOR ゲートが必要な場合は、複数の 2 入力 XOR ゲートを単純に組み合わせて、目的の XOR ゲートを取得します。
トランジスタを用いたXORゲートの構築
排他的な実装が可能 ORゲート トランジスタを使って。以下は、XOR 演算を実装するために組み合わせられるさまざまな回路要素の接続を示す回路です。
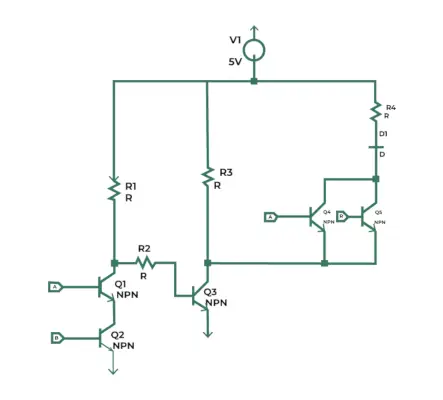
NPNトランジスタを使用したXORゲート
回路の働き
2 入力 XOR ゲートの場合の入力のさまざまなシナリオを利用して、この回路を理解します。
ケース I: 両方の入力がゼロの場合。 (A=0、B=0)
入力 A と B の両方がゼロの場合、 トランジスタ Q1、Q2、Q4、および Q5 はオープン回路であるため、Q4 と Q5 の両方がオープンであり、LED のマイナスピンがグランドに接続されていないため、LED は点灯しません。
htmlリストボックス
ケース II: 一方の入力が論理 High で、もう一方の入力が論理 Low の場合 (A=1、B=0)
この場合、Q4 が現在閉回路として機能していることが簡単にわかります。したがって、LEDのマイナスピンはQ4を介してQ3に接続され、最終的にはグランドに接続されるため、この場合LEDが点灯します。
ケース III – 一方の入力が論理 High で、もう一方の入力が論理 Low の場合 (A=0、B=1)
この場合、Q5 が閉回路として動作していることが簡単にわかります。したがって、LEDのマイナスピンはQ5を介してQ3に接続され、最終的にはグランドに接続されるため、この場合LEDが点灯します。
ケース IV – 両方の入力が論理 High の場合。 (A=1、B=1)
この場合、A と B の両方が論理 High の場合、トランジスタ Q1 と Q2 もアクティブになり、電流は +5V 接合部から Q1 と Q2 トランジスタを通って直接グランドに流れ、Q3 が接続されている経路には入りません。その結果、トランジスタQ3は開回路として機能し、最終的には負のピンとして機能します。 導かれた アースから切り離されているため、LED は点灯しません。
a-b 剪定
XORゲートの応用例
XOR ゲートのアプリケーションの一部を次に示します。
- データ暗号化: XOR ゲートはデータ暗号化アルゴリズムで使用されます。データと秘密キーを組み合わせてスクランブルをかけるために使用されるため、権限のない人による解読は非常に困難になります。
- コンパレータ回路: 比較回路で 2 つのバイナリ値が等しいかどうかをチェックするために使用されます。両方の入力が同じタイプの場合は出力 0 が与えられ、異なる入力の場合は出力 1 が与えられます。
- バイナリの加算と減算: 各ビットの合計を決定したり、他のビットと組み合わせたりするのに役立ちます。 論理ゲート 借用操作を処理します。
- フリップフロップを切り替えます: で Tフリップフロップ クロックパルスが通過するたびにトグルする回路に使用されます。
XOR ゲートのその他の用途には、アドレスのデコード、セキュリティとアクセス制御、乱数の生成、 クロック同期 、分周回路など。
XORゲートのメリットとデメリット
XOR ゲートの長所と短所のリストを以下に示します。
XORゲートの利点
- 一連の入力に奇数の「1」があるかどうかを検出するのに役立ちます。
- XOR ゲートは、排他的 OR 演算を実行します。これは、XOR ゲートウェイの基本的な演算です。 デジタルロジック 。
XORゲートの欠点
- XORゲートは複雑なゲート回路であり、弊社使用回路に接続すると消費電力が増加し、回路が複雑になります。
- の増加につながります。 伝播遅延 回路の。
- 入力の数が増えると、回路はますます複雑になり、エラーの維持と検出が困難になります。
XOR ゲートの解決例
その 1 つの要素を除いて、すべての要素が 2 回出現すると仮定して、一連の数値から 1 つの数値を見つけます。
解決: 2 つの同じビットの XOR は「0」になることがわかっているので、要素を XOR すると、2 回出現するすべての要素が「0」になり、残りの要素だけが答えになることがわかります。
[7,2,2,3,3,4,4,5,5,6,6] のうちのようなもの
上記の各要素を XOR すると、偶数回出現する要素は「0」を返し、奇数回出現する要素は出力を与えます。この要素のみが 1 回だけ発生し、残りの要素は偶数回発生するため、最終的に出力として 7 が得られます。
結論
この記事では、XOR ゲートについて学びました。 XOR ゲートは入力としてブール値を受け取り、論理 High 入力の数が奇数の場合は「1」を返し、論理 High 入力の数が偶数の場合は 0 を返します。
この記事では、真理値表、記号表現、解決例、および記事の理解を深めるのに役立つアプリケーションについて説明します。
文字列.値
XOR ゲート – FAQ
XORゲートはユニバーサルロジックゲートですか?
No XOR ゲートは汎用論理ゲートではありませんが、汎用論理ゲートを使用して実装できます。
XOR と XNOR が特別なゲートであるのはなぜですか?
XOR ゲートと XNOR ゲートは特別です。 排他的な操作を実行する エラーの検出、訂正、バイナリ演算に不可欠であり、デジタル ロジックとコンピューティングの基礎となります。
2入力のXORとは何ですか?
2 入力の場合、 XOR (排他的論理和) ゲートは、入力の一方が 1 でもう一方が 0 の場合にのみ 1 を出力します。両方の入力が同じ場合、出力は 0 です。
XORの記号は何ですか?
排他的論理和(XOR)の記号は⊕です。
XOR は 4 つの入力を持つことができますか?
はい、XOR ゲートには 3 つ以上の入力を含めることができます。の場合 4入力XORゲート、 奇数の入力が 1 の場合、出力は 1 です。入力内の 1 の数が偶数の場合、出力は 0 になります。
XOR ゲートは加算と減算に使用できますか?
はい、XOR ゲートを他の論理ゲートおよびキャリー回路と組み合わせると、バイナリ加算および減算を実行するために使用できます。これらは二項算術演算に不可欠なコンポーネントです。
XOR ゲートはバイナリ ロジックと真理値表に関してどのように動作しますか?
XOR ゲートは、バイナリ加算モジュロ 2 (ビット単位の排他的 OR) と同様の動作を示し、バイナリ データの比較と操作に使用されます。
