統計における Z スコア - データサイエンス

統計における Z スコア データポイントが分布の平均からどれだけ標準偏差があるかを測定したものです。統計で Z スコアを見つけてみましょう。 Z スコア 0 は、データポイントのスコアが平均スコアと同じであることを示します。正の Z スコアはデータポイントが平均より高いことを示し、負の Z スコアはデータポイントが平均より低いことを示します。

Z スコアを計算する式は次のとおりです。 z = (x – μ)/p

どこ：

バツ： はテスト値です
メートル: 平均です
で：は標準値です

この記事では、次の概念について説明します。

Zスコアとは何ですか?
Zスコアを計算するにはどうすればよいですか?
Zスコアの特徴
Z スコア値を使用して外れ値を計算する
Python での Z スコアの実装
Zスコアの適用
Z スコアと標準偏差
Z スコアが標準スコアと呼ばれるのはなぜですか?

Zスコアとは何ですか?

Z スコアは標準スコアとも呼ばれ、平均を上回るまたは下回る標準偏差で表すことによって、平均からのデータポイントの偏差を示します。これにより、データポイントが平均からどの程度離れているかがわかります。したがって、Z スコアは平均からの標準偏差で測定されます。たとえば、Z スコア 2 は、値が平均から 2 標準偏差離れていることを示します。 Z スコアを使用するには、母平均 (μ) と母標準偏差 (σ) を知る必要があります。

Z スコアの計算式

Z スコアは、次の式を使用して計算できます。

YouTubeビデオをダウンロードするvlc

z = (X – μ) / p

どこ、

z = Z スコア
X = 要素の値
μ = 母集団の平均
σ = 母集団標準偏差

Zスコアを計算するにはどうすればよいですか?

問題文で母平均 (μ)、母標準偏差 (σ)、および観測値 (x) が与えられ、それを Z スコア方程式に代入すると、Z スコア値が得られます。指定された Z スコアが正か負かに応じて、次のように使用できます。正の Z テーブルまたは負の Z テーブルオンラインまたは統計教科書の裏の付録で入手できます。

例 1:

あなたは GATE 試験を受けて 500 点を取りました。GATE の平均点は 390 点で、標準偏差は 45 でした。平均的な受験者と比較して、テストの得点はどのくらいでしたか?

解決：

以下のデータは、上記の質問文ですぐに入手できます。

生のスコア/観察値 = X = 500

平均スコア = μ = 390

標準偏差 = σ = 45

Zスコアの公式を適用すると、

z = (X – μ) / p

z = (500 – 390) / 45

z = 110 / 45 = 2.44

これは、Z スコアが 2.44 。

Z スコアは正の 2.44 であるため、正の Z テーブルを使用します。

では、見てみましょう Zテーブル (CC-BY) 他の受験者と比較して自分の得点がどのくらいかを知るため。

表から確率を求めるには、次の手順に従ってください。

ここ、 Z スコア = 2.44、 どれの私データポイントが平均より 2.44 標準偏差上にあることを示します。

まず、最初の 2 桁 2.4 を Y 軸にマッピングします。
次に、X 軸に沿って、0.04 をマップします。
両方の軸を結合します。 2 つの交差により、探している Z スコア値に関連する累積確率が得られます。

[この確率は、Z スコアの左側の標準正規曲線の下の領域を表します]

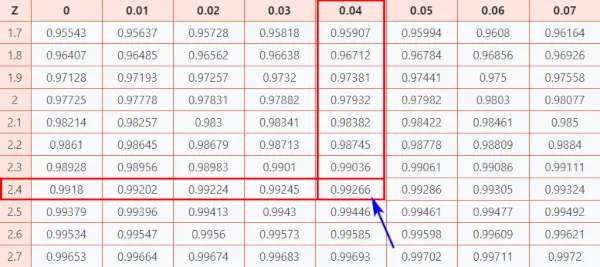
正規分布表

その結果、最終的な値が得られます。 0.99266 。

特殊文字の名前

ここで、GATE 試験の元のスコア 500 とバッチの平均スコアを比較する必要があります。これを行うには、Z スコアに関連付けられた累積確率をパーセンテージ値に変換する必要があります。

0.99266 × 100 = 99.266%

最後に、ほぼ以上のパフォーマンスを発揮したと言えます。 99% 他の受験者のこと。

例 2 : 生徒の得点が 350 ～ 400 点になる確率はどれくらいですか (平均得点 μ が 390、標準偏差 σ が 45)。

解決：

最小スコア = X₁= 350

最大スコア = X₂= 400

Zスコアの公式を適用すると、

と₁= (X1 – m) / p
文字列を int java にキャストします

と₁= (350 – 390) / 45

と₁= -40 / 45 = -0.88

と₂= (X₂– m) / p

z2 = (400 – 390) / 45

と₂= 10 / 45 = 0.22

z1 は負なので、負の値を調べる必要があります。 Zテーブルそして、最初の確率である累積確率 p1 が 0.18943 。

と₂は正であるため、累積確率 p を生成する正の Z テーブルを使用します。₂の 0.58706 。

最終的な確率は、p から p1 を引くことによって計算されます。₂:

p = p₂–p₁

p = 0.58706 – 0.18943 = 0.39763

生徒の得点が 350 ～ 400 点である確率は次のとおりです。 39.763% (0.39763 * 100)。

Zスコアの特徴

Z スコアの大きさは、データポイントが標準偏差の観点から平均からどれだけ離れているかを反映します。
0 未満の Z スコアを持つ要素は、その要素が平均より小さいことを表します。
Z スコアを使用すると、さまざまな分布からのデータポイントを比較できます。
0 より大きい Z スコアを持つ要素は、その要素が平均より大きいことを表します。
Z スコアが 0 に等しい要素は、その要素が平均に等しいことを表します。
1 に等しい Z スコアを持つ要素は、その要素が平均より 1 標準偏差大きいことを表します。 Z スコアが 2 に等しい、標準偏差が平均より 2 つ大きい、などです。
-1 に等しい Z スコアを持つ要素は、その要素が平均より 1 標準偏差小さいことを表します。 Z スコアは -2、平均より標準偏差 2 つ小さいなどです。
特定のセット内の要素の数が多い場合、要素の約 68% の Z スコアは -1 から 1 の間になります。約 95% の Z スコアは -2 ～ 2 です。約 99% の Z スコアは -3 ～ 3 です。これは経験則として知られており、以下の図に示すように、正規分布における平均から一定の標準偏差以内にあるデータの割合を示します。

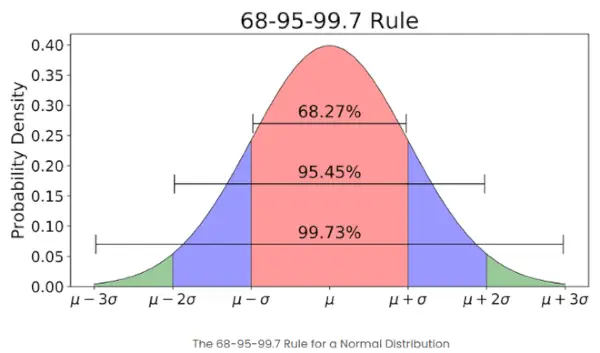
正規分布における経験則

Z スコア値を使用して外れ値を計算する

データポイントの Z スコア値を使用して、データ内の外れ値を計算できます。外れ値データポイントを考慮する手順は次のとおりです。

まず、外れ値を確認したいデータセットを収集します
データセットの平均と標準偏差を計算します。これらの値は、各データポイントの Z スコア値を計算するために使用されます。
各データポイントの Z スコア値を計算します。 Z スコア値の計算式は次と同じになります。
Z = frac{{X – mu}}{{sigma}}
ここで、X はデータ点、μ はデータの平均、σ はデータセットの標準偏差です。
データポイントが外れ値と見なされる Z スコアのカットオフ値を決定します。このカットオフ値は、プロジェクトに応じて決定するハイパーパラメーターです。
Z スコア値が 3 より大きいデータポイントは、そのデータポイントがデータセットの 99.73 % ポイントに属していないことを意味します。
Z スコアが決定したカットオフ値より大きいデータポイントは外れ値とみなされます。

チェック： 外れ値検出の Z スコア

Python での Z スコアの実装

Python を使用して、データセット内のデータポイントの Z スコア値を計算できます。また、numpy ライブラリを使用して、データセットの平均と標準偏差を計算します。

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
データセット内の外れ値は {外れ値}')>>

出力：

Z スコア: [-0.7574907 -0.59097335 -0.20243286 0.35262498 0.6301539 -0.72973781
-0.70198492 -0.00816262 0.13060185 0.54689523 1.10195307 3.32218443
-0.67423202 -0.64647913 -0.61872624 -0.59097335 -0.56322046]
データセット内の外れ値は [150] です。

Zスコアの適用

Z スコアは、さまざまな特徴を共通のスケールに合わせるための特徴スケーリングによく使用されます。特徴を正規化すると、平均と単位分散がゼロになることが保証され、これは特定の機械学習アルゴリズム、特に距離測定に依存するアルゴリズムにとって有益です。
Z スコアを使用して、データセット内の外れ値を特定できます。 Z スコアが特定のしきい値 (通常は平均から 3 標準偏差) を超えるデータポイントは、外れ値とみなされる場合があります。
Z スコアは、予想される動作から大幅に逸脱したインスタンスを識別するために、異常検出アルゴリズムで使用できます。
Z スコアを適用すると、歪んだ分布をより正規な分布に変換できます。
回帰モデルを使用する場合、残差の Z スコアを分析して等分散性 (残差の一定分散) をチェックできます。
Z スコアは、平均からの標準偏差を調べることで特徴のスケーリングに使用できます。

Z スコアと標準偏差

Z スコアテクノロジーの長所と短所	標準偏差
生データを標準化されたスケールに変換します。 C++分割文字列	一連の値の変動または分散の量を測定します。
元の測定単位がなくなるため、異なるデータセットの値を比較しやすくなります。	標準偏差は元の測定単位を保持するため、異なる単位を持つデータセット間の直接比較にはあまり適していません。
データポイントが平均からどれだけ離れているかを標準偏差で示し、分布内でのデータポイントの相対位置の尺度を提供します。	元のデータと同じ単位で表現され、値が平均値付近でどの程度広がっているかの絶対的な尺度を提供します。

Z スコア

テクノロジーの長所と短所

標準偏差

生データを標準化されたスケールに変換します。

C++分割文字列

一連の値の変動または分散の量を測定します。

元の測定単位がなくなるため、異なるデータセットの値を比較しやすくなります。

標準偏差は元の測定単位を保持するため、異なる単位を持つデータセット間の直接比較にはあまり適していません。

データポイントが平均からどれだけ離れているかを標準偏差で示し、分布内でのデータポイントの相対位置の尺度を提供します。

元のデータと同じ単位で表現され、値が平均値付近でどの程度広がっているかの絶対的な尺度を提供します。

チェック： Zスコアテーブル

Z スコアが標準スコアと呼ばれるのはなぜですか?

Z スコアは、確率変数の値を標準化するため、標準スコアとも呼ばれます。これは、標準化スコアのリストの平均が 0、標準偏差が 1.0 であることを意味します。 Z スコアを使用すると、さまざまな種類の変数のスコアを比較することもできます。これは、相対的な順位を使用して、さまざまな変数または分布からのスコアを同等にしているためです。

Z スコアは、変数を標準正規分布 (μ = 0 および σ = 1) と比較するためによく使用されます。

統計における Z スコア – FAQ

正の Z スコアと負の Z スコアにはどのような意味がありますか?

正の Z スコアは平均を上回る値を示し、負の Z スコアは平均を下回る値を示します。符号は平均からの偏差の方向を表します。

Z スコア 0 は何を意味しますか?

Z スコア 0 は、データポイントの値がデータセットの平均値に正確に一致していることを示します。これは、データポイントが平均を上回ったり下回ったりしていないことを示しています。

Z スコアに関する 68-95-99.7 ルールとは何ですか?

経験則としても知られる 68-95-99.7 ルールには、次のように記載されています。

データの約 68% が平均から 1 標準偏差以内に収まります。
約 95% は 2 標準偏差以内に収まります。
約 99.7% は 3 標準偏差以内に収まります。

Z スコアは非正規分布に使用できますか?

Z スコアは、データが正規分布に従うという前提に基づいています。ただし、実際には、Z スコアは正規分布に従うデータに有益です。 Z スコアは任意の分布に対して計算できますが、非正規分布のデータを扱う場合、その解釈の信頼性が低くなり、単純になります。

Z スコアは実際の状況にどのように適用できますか?

Z スコアは、ポートフォリオ分析のための金融、標準化されたテストのための教育、臨床評価のための健康など、さまざまな用途に使用できます。これらは、データを比較および解釈するための標準化された尺度を提供します。