多項式のゼロ これらの実数値、虚数値、または複素数値を変数の代わりに多項式に入れると、結果はゼロになります (名前が示すとおり、ゼロになります)。多項式は、実生活で起こるいくつかの物理現象をモデル化するために使用され、状況を数学的に説明するのに非常に役立ちます。

多項式のゼロは、多項式をゼロにするすべての x 値です。多項式のゼロは、多項式のグラフの x 切片を示します。この記事では、 多項式のゼロ、その求め方、因数定理など。

目次

• 多項式のゼロとは何ですか?
• 多項式のゼロ
• 多項式のゼロを見つけるにはどうすればよいですか?
• 線形多項式の場合
• 二次多項式の場合
• 3次多項式の場合
• 因数定理
• ゼロと係数の関係
• 二次方程式のゼロと係数の関係
• 3次方程式のゼロと係数の関係
• 多項式のゼロを使用した方程式の作成
• 多項式のグラフのゼロ
• 線形代数の基本定理
• ルートの多重度
• 多項式のゼロに関する記事
• 多項式のゼロに関するサンプル問題
• 多項式のゼロに関する練習問題

多項式のゼロとは何ですか?

多項式 P(x) について、P(a) = 0 の場合、x = a が多項式のゼロであると言い、多項式のそのようなゼロはすべて、一般に多項式のゼロと呼ばれます。たとえば、f(x) = 3x – 12 を考えてみましょう。ここで、多項式に x = 4 を入れます。つまり、f(4) = 3×4 – 12 = 0 となります。したがって、x = 4 は多項式 f( x) = 3x – 12。

例: f(x) = x の場合 ³ – 6倍 ² + 11x – 6、x = 1 はゼロですか?

解決：

f(x) = x の x = 1 がゼロかどうかを確認するには³– 6倍²+ 11x – 6 かどうか、(x) に x = 1 を入れます

f(1) = (1)³– 6×(1)²+11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

したがって、x = 1 は f(x) のゼロです。

多項式のゼロ

ax + b の形式の線形多項式の場合、そのゼロは x = -b/a で与えられます。

ax 形式の 2 次多項式の場合²+ bx + c、そのゼロは x = {- b ± √D}/2a で与えられます。ここで、D は b で与えられる判別式です。²– 4ac。

多項式のゼロを見つけるにはどうすればよいですか?

以下で説明するさまざまな方法を使用して、さまざまなタイプの多項式の多項式のゼロを見つけることができます。

• 線形多項式の場合
• 二次多項式の場合
• 3次多項式の場合

線形多項式の場合

線形多項式の場合、ゼロを見つけるのが最も簡単です。ゼロは 1 つだけであり、多項式を 0 に等しくした後、多項式を単純に並べ替えることでも計算できます。

たとえば、線形多項式 f(x) = 2x – 7 のゼロを見つけます。

解決：

f(x) のゼロを見つけるには、f(x) を 0 と同等とします。

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

二次多項式の場合

二次多項式の根やゼロを求めるには、シュリー・ダラチャリヤ公式としても知られる二次公式である中間項を分割する方法や、二次公式が登場するように二次公式に似た二乗を完成させる方法など、さまざまな方法があります。一般的な二次方程式の平方完成から。

詳しくはこちら 二次方程式を解く または多項式とその解き方。次の例は、二次多項式のゼロを見つける方法を詳細に示しています。

例 1: P(x) = x のゼロを見つけます。 ² + 2x – 15。

答え：

バツ²+ 2x – 15 = 0

⇒ ײ+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3、-5

例 2: P(x) = x のアウトゼロを見つける ² – 16x + 64。

答え：

バツ²– 16x + 64 = 0

斧との比較²+ bx + c = 0、

a = 1、b = -16、c = 64 となります。

したがって、

⇒ x = 8, 8

ウェブブラウザの設定

3次多項式の場合

3次のゼロを見つけるには、有理根定理や長い除算を一緒にするなど、多くの方法があります。 3 次多項式またはそれ以上の多項式の根を求める 1 つの方法は次のとおりです。

ステップ1： 有理根定理を使用して、考えられる根を見つけます。つまり、多項式に有理根がある場合、それは p/q の除算でなければなりません。ここで、p は整数定数、q は先頭の係数です。

ステップ2： 1 つの根を見つけたら、多項式をその根によって形成される因数で長除算を使用して割り、多項式を商と被除数の積として書き込みます。

ステップ 3: 商が二次式の場合は、二次多項式について前述した方法でそれを解きます。次数 2 の多項式でない場合は、商が次数 2 の多項式になるまで手順 1 と 2 を繰り返します。

ステップ 4: ステップ 3 の結果が必要な因数であり、その因数を 0 とみなすことで、多項式のゼロを見つけることができます。

例: 3 次多項式のゼロ点を見つける p(x) = x ³ +2倍 ² – 5x – 6.

解決：

p(x) = x³+2倍²– 5x – 6

p/q = -6 として

有理根定理により、多項式の考えられるすべての有理根は p/q の約数になります。

したがって、約数 = ±1、±2、±3、±6

x = -1、p(x) では、次のようになります。

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

したがって、因数定理により、x + 1 は p(x) の因数です。

したがって、x³+2倍²– 5x – 6 = (x+1)(x²+x – 6)

⇒ ׳+2倍²– 5x – 6 = (x+1)(x-2)(x+3)

ゼロの場合、p(x) = 0、

p(x) のゼロは、x = -1、x = 2、および x = -3 です。

因数定理

多項式 P(x) の場合、因数定理は、x – a が P(x) の因数である場合、x =a が P(X) のゼロであることを示します。つまり、次の両方の条件が当てはまる必要があります。

• a が P(x) のゼロの場合、x−a は P(x) の因数になります。
• x−a が P(x) の因数である場合、a は P(x) のゼロになります。

これは、前の例を見ることで確認できます。因数定理は、次のような興味深い結果をもたらす可能性があります。

結果 1: P(x) が n 次の多項式で、r が P(x) のゼロである場合、P(x) は次の形式で書くことができます。

P(x) = (x – r) Q(x)

ここで、Q(x) は n-1 次の多項式であり、P(x) を (x – r) で除算することで求められます。

結果 2: P(x) = (x-r)Q(x) で、x = t が Q(x) のゼロの場合、x = t も P(x) のゼロになります。

上記の事実を確認するには、

t がゼロ Q(x) であるとします。これは、Q(t) = 0 を意味します。

r は多項式 P(x) のゼロであることがわかっています。ここで、P(x) = (x – r) Q(x)、

したがって、x = t も P(x) のゼロであるかどうかを確認する必要があります。P(x) に x = t を入れましょう。

⇒ P(t) = (t – r) Q(t) = 0

したがって、x = t もゼロ P(x) です。

したがって、証明されました。

ゼロと係数の関係

二次方程式および三次方程式のゼロと係数の間の関係については、以下で説明します。

二次方程式のゼロと係数の関係

ax 形式の二次方程式の場合²+ bx + c = 0、二次方程式の 2 つのゼロが α と β の場合、

• ルートの和 = α + β = -b/a
• 根の積 = α × β = c/a

3次方程式のゼロと係数の関係

α、β、γ が 3 次多項式 ax の根である場合³+bx²+ cx + d = 0 の場合、そのゼロと係数の関係は次のようになります。

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

多項式のゼロを使用した方程式の作成

• ゼロ α と β を持つ 2 次多項式の場合、2 次多項式は次のように与えられます。

バツ ² – (a + b)x + ab 。

• 3 つのゼロ α、β、γ を持つ 3 次多項式の場合、3 次多項式は次のように求められます。

バツ ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

多項式のグラフのゼロ

多項式 y = f(x) のグラフでは、実ゼロはグラフが x 軸と交差するか接触する点です。 (虚数ゼロを含むグラフは x 軸を切ることはありません)。言い換えると、3次多項式の実数解が3つある場合、その3次多項式のグラフはx軸と3回交差しますが、ある3次多項式の実数解が1つしかない場合、グラフはx軸を切り取るだけです。一度。

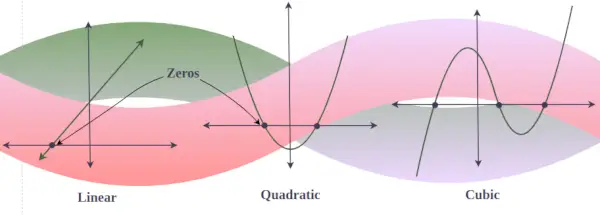
線形代数の基本定理

P(x) が n 次の多項式の場合、P(x) は正確に n 個のゼロを持ち、その一部は繰り返される可能性があります。

Javaでcsvファイルを読み取る

これは、すべてのゼロをリストし、それぞれを k 回リストすると、その多重度が k であることを意味します。リストには正確に n 個の数値が含まれます。これは、多項式にゼロがいくつあるべきかについてのアイデアを得ることができるので便利です。したがって、必要なゼロの数に達したら、ゼロの検索を停止できます。

ルートの多重度

因数分解される多項式 P(x) = 0 があるとします。

P(x) = (x – r) ^k (x – a) ^メートル

r が多項式のゼロであり、根を生成した項の指数が k である場合、r は次のようになります。 多重度k 。多重度 1 のゼロはよく呼ばれます。 単純 ゼロと多重度 2 のゼロは、多項式の二重根と呼ばれます。

例: P(x) は 5 次多項式であり、因数分解されています。ルートとその多重度をリストします。

P(x) = 5x ⁵ −20倍 ⁴ +5倍 ³ +50倍 ² −20x−40=5(x+1) ² (x−2) ³

解決：

与えられた場合、P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

ゼロを見つけるには、P(x) = 0

⇒ x = -1、-1、2、2、2

-1 はゼロとして 2 回出現するため、その多重度は 2 ですが、ゼロ 2 の多重度は 3 であることに注意してください。

多項式のゼロに関する記事

• 多項式
• 二次方程式の根
• 代数式

多項式のゼロに関するサンプル問題

問題 1: x = 2 が P(x) = x のゼロであると仮定します。 ³ +2倍 ² −５×−６。残りの 2 つのゼロを見つけます。

解決：

先ほど学習した基本定理から、P(x) は 3 次多項式であるため、3 つのゼロを持つと言えます。そのうちの 1 つは x = 2 です。

したがって、P(x) を書き直すと、

P(x) = (x – 2) Q(x)

他の 2 つのゼロを見つけるには、Q(x) を見つける必要があります。

Q(x) は、P(x) を (x-2) で割ることによって求められます。

除算すると、Q(x) は次のようになります。

Q(x) = x²+ 4x + 3

残りの 2 つのゼロはこれからわか​​ります。

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0、

x = -1、-3

したがって、他の 2 つのゼロは x = -1 と x = -3 になります。

問題 2: x = r が多項式のゼロであるとすると、多項式の他のゼロを見つけます。

P(x) = x ³ -6x ² −16倍。 r = −2

解決：

x = -2 がゼロであることはわかっていますが、

したがって、P(x) は次のように書き換えることができます。 P(x) = (x + 2) Q(x) {除算アルゴリズムを使用する}

ここで Q(x) を求めるには、前の質問で行ったのと同じことを行い、P(x) を (x + 2) で除算します。

我々が得る、

Q(x) = x²– 8x

残りの 2 つのゼロを見つけるには、Q(x) を因数分解します。

Q(x) = x (x – 8) = 0

したがって、ゼロは x = 0、8 です。

したがって、3 つのゼロ、x = -2、0、8 があります。

問題 3: 多項式 4x のゼロを求めます ³ -3x ² -25x-6 = 0

解決：

3次の多項方程式を解くコツ、

1、-1、2 などから始めて、多項式の値を 0 にすることができる最小の整数を見つけます。

x = -2 の場合、expression の値がゼロになることがわかります。

したがって、根の 1 つは -2 です。

因数定理に従って、a が多項式のゼロの 1 つである場合、(x-a) は指定された多項式の因数になります。

したがって、この {x – (-2)} = (x+2) に続くのは、多項式上の係数 p です。

二次方程式が得られ、ゼロがすでにそこにあります。

(4x²-11x-3)(x+2) = 0

二次方程式を因数分解すると、

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2、x = 3、x = -1/4

問題 4: 多項式 4x のゼロを求めます ⁶ – 16倍 ⁴ = 0

解決：

多項式には次数が 6 まであるため、多項式のゼロが 6 つ存在します。

4倍⁴（バツ²-4) = 0

4倍⁴（バツ²-2²) = 0

4倍⁴[(x+2)(x-2)] = 0

したがって、x= 0、0、0、0、2、-2

問題 5: 多項式関数 f(x) = x のゼロ点を求めます。 ³ – 2倍 ² – 5x + 6

解決：

この多項式のゼロを見つけるには、f(x) = 0 を設定し、x を求めます。

f(x) = x³– 2倍²– 5x + 6 = 0

d/a = 6 として

有理根定理によると、多項式の考えられるすべての有理根は次のようになります。

d/a の約数 = ±1、±2、±3、±6

x = 1、p(x) では、次のようになります。

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

したがって、因数定理により、x – 1 は p(x) の因数です。

したがって、x³+2倍²– 5x – 6 = (x-1)(x²-x – 6)

バツ³+2倍²– 5x – 6 = (x-1)(x+2)(x-3)

ゼロの場合、p(x) = 0、

p(x) のゼロは、x = 1、x = -2、および x = 3 です。

多項式のゼロに関する練習問題

1. 多項式 f(x) = x のすべてのゼロを見つけます。 ³ – 6倍 ² + 11x – 6

2. 多項式 g(x) = 2x のすべてのゼロを決定します。 ⁴ – 7倍 ³ +3倍 ² + 4x – 4

3. 多項式 h(x) = x のゼロ点を見つけます。 ⁵ – 3倍 ⁴ +2倍 ³ – 6倍 ² + x + 2

4. 多項式のすべてのゼロを決定します p(x) = 3x ⁴ – 16倍 ³ +18倍 ² + 16x – 12。

多項式のゼロに関する FAQ

多項式のゼロとは何ですか?

このような実数値は、多項式の値が 0 になるため、つまり、p(x) が多項式で p(a) = 0 の場合、x = a は p(x) のゼロになります。

多項式のゼロを見つけるにはどうすればよいですか?

二次方程式の中間項や二次方程式など、さまざまな多項式でゼロを見つけるさまざまな方法があります。線形の単純な変数の並べ替えと 3 次の場合は、有理根定理、長除法、因数定理、剰余定理の組み合わせを使用します。

多項式に複数のゼロを含めることはできますか?

はい、多項式には複数のゼロを含めることができます。実際、n 次の多項式には最大で n 個の実ゼロを含めることができます。

多項式のゼロの多重度は何ですか?

因数分解のプロセスでは、多項式の 1 つの因数または 1 つのゼロが、その後、因数またはゼロが来る回数、つまりその根の多重度と呼ばれます。

代数の基本定理とは何ですか?

代数状態の基本定理 P(x) が n 次の多項式である場合、P(x) は正確に n 個のゼロを持ち、その一部は繰り返される可能性があります。

次数 n の多項式は常に n の実根を持ちますか?

いいえ、根の一部が虚数または複素数になる可能性があるため、次数 n の多項式には常に n 個の実根があるとは限りません。

ゼロ多項式の次数とは何ですか?

ゼロ多項式の次数はゼロです。

ピリオドキー