加速度は速度の時間変化です。現実のシナリオでは、加速度も時間とともに変化します。たとえば、ある都市から別の都市へ陸路で移動しているとします。この場合、道路が空いている場合はさらに加速し、渋滞している場合は加速して下降します。この加速度の変化は、時間に対する加速度をグラフにプロットすることで観察できます。これを加速時間グラフといいます。この記事では、加速時間グラフについて詳しく学び、それに基づいて問題を解決します。
sqrt Java数学
加速時間グラフとは何ですか?
加速時間グラフを使用して、次の関係を表します。 加速度 ここで、加速度は Y 軸にプロットされる独立変数、時間は X 軸にプロットされる従属変数です。物体の動きを観察し、得られた加速度と時間のデータを長方形のグラフ上にプロットすると得られます。加速時間グラフを利用して、特定の時間間隔における速度の変化を判断できます。加速度-時間グラフの曲線の下の面積を決定することにより、運動している物体の一定期間にわたる速度の変化を知ることができます。
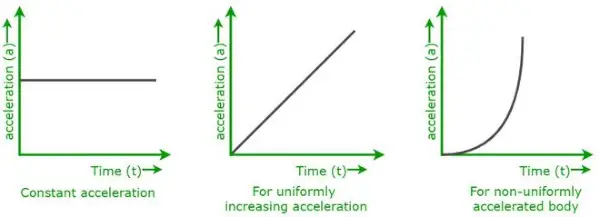
上に示したグラフは、さまざまな種類の体動の加速度-時間のグラフです。
- 物体が一定の加速度で運動しているとき、
- 加速度が増加しながら物体が均一に動いているとき。
- 物体が変化する加速度で不均一に動いているとき。
結論
加速時間グラフから得られるポイントは以下のとおりです。
- 加速時間グラフの傾きは△a/△tです。
- 加速時間グラフの下の領域は速度の変化を表します。
させて、
△v 速度の変化であり、
△あ 加速度の変化であり、
△t 時代の変化であろう。
今、 曲線の下の面積 = △v
物体の加速度は、一定期間内の速度の変化率と呼ばれることがわかっています。
それで、
△a = △v/△t
さて、両辺に△tを掛けると、
△v = △a × △t (v これは加速時間の曲線下の面積です グラフ )
- 一定の加速度で移動する物体の場合、つまり加速度はどの時間間隔でも同じです。したがって、加速時間グラフの傾きはゼロとなり、グラフは時間軸と平行になります。
加速度と減速度

加速度: 物体の加速度は、一定期間内の速度の変化率と呼ばれます。これはベクトル量であり、m/s の単位で測定されます。2。
加速度 = 速度の変化/時間
ここで、速度の変化は正です。
等速で移動する物体が速度を増すと仮定します。速度の増加率を物体の加速度といいます。 u を初速度、v を最終速度、t を時間間隔とすると、物体の加速度は次のように与えられます。
加速度 (a) = (v – u)/t
例: 日常生活における加速の例としては、車がコーナーで曲がることがあります。方向が変わると車の速度が増加し、加速が生じます。旋回速度が上がると加速も増します。
リタデーション: 物体の遅滞は、一定期間内の速度の変化率と呼ばれます。遅角とは負の加速度を意味します。
リターデーション = 速度の変化/時間
ここで、速度の変化は負です。
等速で移動している物体が速度を落とすと仮定します。速度の減少率は物体の遅滞と呼ばれます。 u を初速度、v を最終速度、t を時間間隔とすると、物体の遅速度は次のように与えられます。
リタデーション = (v – u)/t
例: 遅延の実例としては、扇風機を止めることが挙げられます。可動ファンのスイッチがオフになると、ファンブレードの回転速度が徐々に遅くなります。ファンの速度のこの減少率は遅延として知られています。
こちらもチェックしてください:
- 距離時間グラフ
- 速度時間グラフ
加速時間グラフの問題例
問題 1: 以下の加速度と時間のグラフから、速度の変化を求めます。

解決:
物体の速度の変化を見つけるには、曲線の下の領域を決定する必要があります。
したがって、物体の速度の変化を見つけるには、三角形の面積を計算する必要があります。
△v = 三角形の面積
= 1/2 × 25 × 6
△v=75m/s。
したがって、速度の変化は 75 m/s です。
問題 2: 以下の加速度と時間のグラフから、最終速度が 55 m/秒の場合の物体の初速度を求めます。

解決:
物体の速度の変化を見つけるには、曲線の下の領域を決定する必要があります。グラフから、長方形と三角形があることがわかります。したがって、物体の速度の変化を知るには、これらの図形の面積を計算する必要があります。
△v = 三角形の面積 + 長方形の面積
= 1/2 × 8 × 6 + 2 × 8
△v = 24 + 16 = 42 m/s
私達はことを知っています、
△v = 最終速度 – 初速度
42 = 55 – インチ私
で私= 55 – 42 = 13 m/秒
したがって、初速度は 13 m/s になります。
問題 3: 以下の加速度と時間のグラフから、v(0) = 0 の場合、t = 6 秒での速度を求めます。

解決:
加速度は次の式で与えられます。
a = dv/dt
⇒ dv = (a)dt
両側を積分すると、次のようになります。
∫dv = ∫(a) dt
⇒ v = ∫(1.5) dt
⇒ v(t) = 1.5t + c、c は定数
⇒ v(0) = 0
⇒ c = 0
ここで、v(t) = 1.5t
v(6) = 1.5 × 6 = 9 m/s
したがって、t = 6 秒での速度は 9 m/s です。
問題 4: 加速時間グラフの下の領域は何を示していますか?
解決:
加速時間グラフの下の領域は速度の変化を表します。
速度の変化を△v、加速度の変化を△a、時間の変化を△tとします。
さて、曲線の下の面積 = △v
物体の加速度は、一定期間内の速度の変化の比率として参照されることがわかっています。
それで、
△a = △v/△t
さて、両辺に△tを掛けると、
△v = △a × △t
したがって、曲線の下の面積は、加速度の変化と時間の変化を乗じることによって得られます。
問題 5: 加速時間グラフのジャークは何を意味しますか?
解決:
躍動感は移動体の加速度の急激な変化であり、a-t グラフの傾きが躍動感を表します。
加速時間グラフの傾き=ジャーク=△a/△t
加速時間グラフ – FAQ
加速時間グラフとは何ですか?
加速時間グラフは、直線で移動する物体の加速度が時間の経過とともにどのように変化するかを表示します。 X 軸の時間に対して、Y 軸に加速度をプロットします。
加速時間グラフの下の面積はどのように計算されますか?また、それは何を表しますか?
加速時間グラフの下の領域は、グラフがカバーする期間にわたる速度の変化を表します。この面積を計算するには、通常、加速度が一定である個別の時間間隔に対応する、曲線の下に収まる長方形または台形の面積を合計します。
加速時間グラフから特定の時間における物体の速度を決定できますか?
加速時間グラフから特定の時刻における瞬間速度を直接求めることはできません。ただし、その期間内のグラフの下の面積を見つけることで、一定期間にわたる速度の変化を計算できます。初速度がわかれば、最終速度を決定することができます。
このタイプのグラフで負の加速度は何を示していますか?
加速時間グラフの負の加速度は減速を示し、オブジェクトが正の方向に移動している場合、オブジェクトの速度は減少します。物体が負とみなされる方向に移動している場合、負の加速度は速度の増加を意味します。
加速時間グラフから平均加速度を見つけるにはどうすればよいでしょうか?
平均加速度は、速度の合計変化 (方向を考慮して曲線の下の領域を合計) を求め、それを合計時間間隔で割ることによって決定できます。視覚的には、これは加速時間グラフの下の総面積に等しい面積を持つ長方形として表すことができます。
加速時間グラフの傾きは何を表しているのでしょうか?
加速時間グラフの傾きは、ジャークとして知られる、時間の経過に伴う加速度の変化率を示します。急な傾斜は加速度の急激な変化を意味します。
静止している物体を加速時間グラフでどのように表現しますか?
静止している物体、または等速度で移動している物体は、加速度ゼロの時間軸に沿った線で加速時間グラフ上に表されます。
加速時間グラフをどのように解釈しますか?
加速時間グラフの傾きは加速度の変化率を表し、傾きが急になるほど変化率が高くなります。
加速時間グラフの下の領域は何を表しますか?
加速時間グラフ上の曲線の下の領域は、物体の速度の変化を表します。具体的には、最終速度から初速度を引いた値を表します。
