速度とは、車をどれくらいの速度で運転するかのように、物体の移動速度の尺度を単純に示したものです。さて、ここでは特定のタイプの速度について話します。角速度は速度の一種にすぎませんが、ここでは物体は円軌道上を移動する必要があります。

角速度の計算式

角速度は、角変位の変化率、つまり円形の経路に沿って物体が通過する角度として定義されます。角速度は、所要時間までに物体が行う回転数/公転数として計算されます。角速度はオメガとして知られるギリシャ文字「ω」で表されます。角速度の SI 単位は rad/s です。

角速度は 2 つの異なる式を使用して計算されます。

ω = θ/t ω = v/r

式の導出

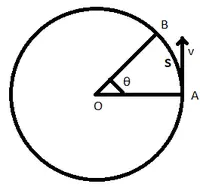
上に示した半径 r の円軌道上を線速度 v で移動する物体を考えてみましょう。物体が点 A から B まで移動し、円弧を通って距離 s を移動し、期間 t で角度 θ を横切るとします。

体で覆われた円形のパス

知られているように、角速度は変位の変化率 – 角速度、ω = θ/t

したがって、角速度の公式は次のようになります。 ω = θ/t 。

角速度の別の公式

上記の公式とは異なり、競技試験の観点から角速度を計算するために、より広く使用されている別の公式があります。

ω = θ/t ⇢ (1) として

これで、円弧を横切って移動した距離は、半径と移動した角度の積に等しいことがわかりました。それで、

s = rθ

=> θ = s/r ⇢ (2)

ブール値から文字列 Java へ

(1)と(2)より、

ω = s/(rt) ⇢ (3)

また、線速度の一般的な理解から、

v = s/t ⇢ (4)

(3)と(4)より、

ω = v/r

サンプル問題

質問 1: 半径 5 メートルの円形の経路に沿って移動する物体を考えてみましょう。 5秒で半回転をカバーします。その角速度を計算します。

解決：

半回転では、横切る角度は 180 度になります。ラジアンでは、π ラジアンに等しくなります。

ω = θ/t

=> ω = π/5 = 0.628 ラジアン/秒

質問 2: 半径 2m の自動車の車輪が 10m/s の線速度で回転しています。角速度を計算してみます。

解決：

ω = v/r

ω = 10/2

= 5 ラジアン/秒

質問 3: 速度 18 km/h、トラック半径 0.2 m の円形トラックを走行するレーシング カーを考えてみましょう。車の角速度を計算します。

解決：

v = 18 km/時 = 5 m/秒

r = 0.2m

ω = v/r

= 5/0.2

= 25 ラジアン/秒

質問 4: 車は半径 2m の円軌道に沿って 2 rad/s の角速度で移動しています。車が 2 秒以内に移動する角度を度単位で計算します。

解決：

考えると、 ω = 2 ラジアン/秒および t = 2 秒

ω = θ/t => θ = ωt なので

=> θ = (2 × 2) = 4 ラジアン

度単位では、θ = 4 × (180/π) = 229.18 度

質問 5: 角速度 7π rad/s の円軌道に沿って移動する物体は、0.5 秒間に何回転しましたか?

解決：

ω = 7π rad/s および t = 0.5s と仮定します。

ω = θ/t => θ = ωt なので

θ = (7π × 0.5) = 3.5π

2π rad では、カバーされる回転数は 1 です

=> 1 rad では、カバーされる回転数は (1/2π) です

=> 3.5π ラジアンでは、回転数 = 3.5π/2π = 1.75 回転

つまり、身体は 0.5 秒以内に 1 回転し、次の 4 分の 3 を完了します。

質問 6: 円弧長 4m、半径 2m の円軌道を 5 秒間移動する物体の角速度はいくらになります。

解決：

s = 4m、r = 2m、t = 5s とすると

式 s = rθ => θ = s/r を使用する

θ = 4/2 = 2 ラジアン

ω = θ/t なので

js セットタイムアウト

=> ω = 2/5 = 0.4 ラジアン/秒