二分木は、木の高さが O(Log n) (n はノードの数) の場合にバランスがとれています。たとえば、AVL ツリーは、左と右のサブツリーの高さの差が最大 1 であることを確認することで、O(Log n) の高さを維持します。赤黒ツリーは、次の数を確保することによって、O(Log n) の高さを維持します。すべての根から葉へのパス上の黒いノードの数は同じであり、隣接する赤いノードはありません。バランス二分探索ツリーは、検索、挿入、削除に O(log n) 時間を提供するため、パフォーマンスの点で優れています。
js オンクリック
バランスの取れた二分木とは、次の 3 つの条件を満たす二分木です。
- どのノードでも、左右のツリーの高さの差は 1 を超えません。
- そのノードの左側のサブツリーもバランスが取れています。
- そのノードの右側のサブツリーもバランスが取れています。
単一ノードは常にバランスが取れています。高さバランスのとれた二分木とも呼ばれます。
例 :
バブルソートPython
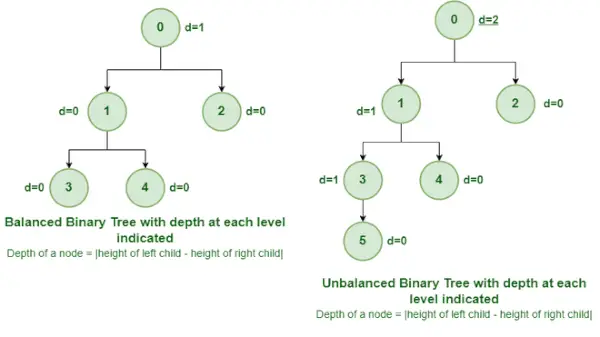
バランスのとれたバイナリ ツリーとアンバランスのバイナリ ツリー
これは、各ノードの左と右のサブツリーの高さの差が 0 または 1 であるバイナリ ツリーの一種です。上の図では、値 0 を持つルート ノードは深さが 2 単位で不均衡です。 。
バランスの取れた二分木の応用:
- AVL ツリー
- レッドブラックツリー
- バランス二分探索ツリー
バランスの取れたバイナリ ツリーの利点:
- 非破壊的な更新は、同じ漸近効果を持つバランス バイナリ ツリーによってサポートされます。
- 範囲クエリと正しいシーケンスでの反復は、バランスのとれたバイナリ ツリーによって実現可能になります。
