まず、次のことを理解します。 二分木 そして 二分探索木 次に、二分木と二分探索木の違いを見ていきます。

二分木とは何ですか?

あ 二分木 です左の子へのポインタ:左の子ノードの参照を格納します。正しい子へのポインタ:右子ノードの参照を格納します。データ要素:データ要素は、ノードによって格納されるデータの値です。

バイナリ ツリーは次のように表すことができます。

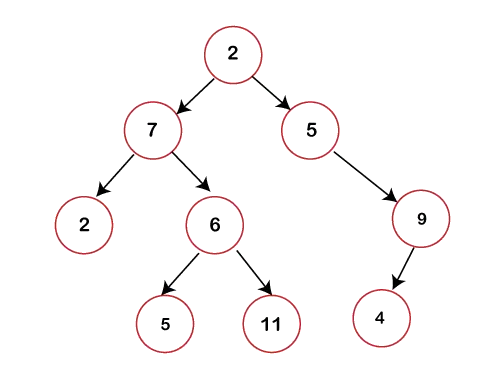
上の図では、各ノードに最大 2 つの子が含まれていることがわかります。どのノードにも左または右の子が含まれていない場合、その子に関するポインタの値は NULL になります。

バイナリ ツリーで使用される基本用語は次のとおりです。

Javaハッシュマップ

ルートノード:ルート ノードは、バイナリ ツリーの最初または最上位のノードです。親ノード:ノードがエッジを介して別のノードに接続されている場合、そのノードは親ノードと呼ばれます。バイナリ ツリーでは、親ノードは最大 2 つの子を持つことができます。子ノード:ノードにその先行ノードがある場合、そのノードは「ノード」と呼ばれます。 子ノード 。リーフノード:として知られる子を含まないノード リーフノード 。内部ノード:少なくとも 2 つの子を持つノードは、 内部ノード 。ノードの深さ:ルート ノードから指定されたノードまでの距離は、 ノードの深さ 。ルート ノードには深さがないため 0 のラベルが付けられ、ルート ノードの子には 1 のラベルが付けられ、ルートの子の子には 2 のラベルが付けられます。身長：ルート ノードからリーフ ノードまでの最長距離は、 ノードの高さ 。

バイナリ ツリーには、 完璧な二分木 。それは すべての内部ノードに 2 つのノードが含まれ、すべてのリーフ ノードが同じ深さである必要があるツリー。完全な二分木の場合、二分木に存在するノードの総数は次の式を使用して計算できます。

n = 2^m+1-1

DFS vs BFS

ここで、n はノードの数、m はノードの深さです。

二分探索木とは何ですか?

あ 二分探索木 は要素を配置するために何らかの順序に従っているツリーですが、バイナリ ツリーはいかなる順序にも従いません。二分探索木では、左側のノードの値は親ノードより小さく、右側のノードの値は親ノードより大きくなければなりません。

例を通して二分探索木の概念を理解しましょう。

上の図では、ルート ノードの値が 15 であり、左側のサブツリー内のすべてのノードの値よりも大きいことがわかります。ルート ノードの値は、右サブツリー内のすべてのノードの値よりも小さくなります。次に、ルート ノードの左の子に移動します。 10 は 8 より大きく 12 より小さいです。また、二分探索木の特性も満たします。ここで、ルート ノードの右の子に移動します。値 20 は 17 より大きく 25 より小さい。また、二分探索木の性質も満たします。したがって、上に示した木は二分探索木であると言えます。

ここで、上記の二分木で 12 の値を 16 に変更した場合、それがまだ二分探索木であるかどうかを調べなければなりません。

ルート ノードの値は 15 であり、10 より大きく 16 より小さいため、二分探索木の特性を満たしていません。したがって、これは二分探索木ではありません。

Cで配列の長さを取得する

二分探索木の操作

二分探索ツリー上で挿入、削除、検索操作を実行できます。二分探索で検索がどのように実行されるかを理解しましょう。検索操作を実行する必要があるバイナリ ツリーを以下に示します。

上記の二分木で 10 を検索する必要があるとします。二分探索を実行するには、ソートされた配列内のすべての整数を考慮します。まず、検索スペース内に完全なリストを作成します。これにより、すべての数値が検索スペース内に存在します。検索スペースは 2 つのポインター、つまり開始と終了によってマークされます。上記の二分木の配列は次のように表すことができます。

まず、中央の要素を計算し、中央の要素と検索対象の要素を比較します。中央の要素は n/2 を使用して計算されます。 n の値は 7 です。したがって、中央の要素は 15 です。中央の要素は、検索された要素、つまり 10 と等しくありません。

注: 検索対象の要素が中間要素よりも小さい場合、検索は左半分で実行されます。それ以外の場合、検索は右半分で行われます。等しい場合、要素が見つかります。

検索対象の要素がmid要素よりも小さいため、左側の配列に対して検索が実行されます。以下に示すように、検索は半分に減りました。

左側の配列の Mid 要素は 10 で、検索された要素と同じです。

時間計算量

二分探索では、要素は n 個あります。中央の要素が検索された要素と等しくない場合、検索スペースは n/2 に削減され、要素が見つかるまで検索スペースを n/2 ずつ削減し続けます。全体のリダクションでは、n から n/2、n/4 などに移動すると、log がかかります。₂n ステップ。

二分木と二分探索木の違い

CSV Javaから読み取る