バイナリヒープ

あ バイナリヒープ です 完全なバイナリツリー これは、データを効率的に保存し、その構造に基づいて最大要素または最小要素を取得するために使用されます。

バイナリヒープは、最小ヒープまたは最大ヒープのいずれかです。最小バイナリヒープでは、ルートのキーはバイナリヒープに存在するすべてのキーの中で最小である必要があります。同じプロパティがバイナリツリー内のすべてのノードに対して再帰的に true である必要があります。 Max Binary Heap は MinHeap に似ています。

最小ヒープの例:

10 10
/ /
20 100 15 30
/ / /
30 40 50 100 40

バイナリヒープはどのように表現されますか?

バイナリヒープとは、 完全なバイナリツリー 。バイナリヒープは通常、配列として表されます。

ルート要素は Arr[0] にあります。
以下の表は、i の他のノードのインデックスを示しています。^番目ノード、つまり Arr[i]:

配列[(i-1)/2]	親ノードを返します
配置[(2*i)+1]	左側の子ノードを返します
配置[(2*i)+2]	右側の子ノードを返します

配列表現を実現するために使用されるトラバーサルメソッドは次のとおりです。 レベル順序のトラバーサル 。を参照してください。バイナリヒープの配列表現詳細については。

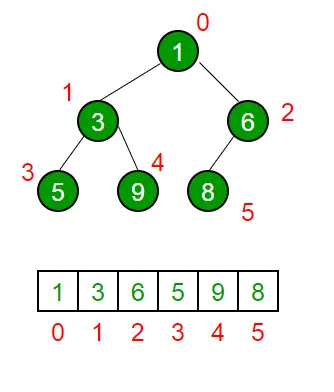
バイナリヒープツリー

ヒープ上の操作:

以下は、最小ヒープに対する標準的な操作の一部です。

getMin(): Min Heap のルート要素を返します。この操作の時間複雑さは、 ○(1) 。 maxheap の場合は次のようになります getMax() 。
extractMin() : MinHeap から最小要素を削除します。この操作の時間複雑さは、 O(log N) この操作ではヒーププロパティを維持する必要があるため (呼び出しによって) heapify() ）根を取り除いた後。
減少キー() : キーの値を減らします。この操作の時間計算量は次のとおりです。 O(log N) 。ノードの減少したキー値がノードの親よりも大きい場合は、何もする必要はありません。それ以外の場合は、上に向かってトラバースして、違反したヒーププロパティを修正する必要があります。
入れる（） : 新しいキーを挿入するには、 O(log N) 時間。ツリーの最後に新しいキーを追加します。新しいキーがその親キーよりも大きい場合は、何もする必要はありません。それ以外の場合は、上に向かってトラバースして、違反したヒーププロパティを修正する必要があります。
消去（） : キーの削除にも時間がかかります O(log N) 時間。呼び出して、削除するキーを最小の無限に置き換えます。 減少キー() 。減少Key()の後、マイナス無限値はルートに到達する必要があるため、呼び出します extractMin() キーを削除します。

以下は基本的なヒープ操作の実装です。

C++

// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>

'
Overflow: Could not insertKey
'>

;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>ハリー[i])>> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>ハリー[i])>> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest != i)   {   swap(&harr[i], &harr[smallest]);   MinHeapify(smallest);   }  }    // A utility function to swap two elements  void swap(int *x, int *y)  {   int temp = *x;   *x = *y;   *y = temp;  }    // Driver program to test above functions  int main()  {   MinHeap h(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   cout << h.extractMin() << ' ';   cout << h.getMin() << ' ';   h.decreaseKey(2, 1);   cout << h.getMin();   return 0;  }>

オペレーティングシステムの例

ジャワ

Javaはinstanceofです

// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0>

&& heapArray[i]   swap(heapArray, i, parent(i));   i = parent(i);   }   return true;   }     // Decreases value of given key to new_val.   // It is assumed that new_val is smaller   // than heapArray[key].   public void decreaseKey(int key, int new_val) {   heapArray[key] = new_val;     while (key != 0 && heapArray[key]   swap(heapArray, key, parent(key));   key = parent(key);   }   }     // Returns the minimum key (key at   // root) from min heap   public int getMin() {   return heapArray[0];   }       // Method to remove minimum element   // (or root) from min heap   public int extractMin() {   if (current_heap_size <= 0) {   return Integer.MAX_VALUE;   }     if (current_heap_size == 1) {   current_heap_size--;   return heapArray[0];   }     // Store the minimum value,   // and remove it from heap   int root = heapArray[0];     heapArray[0] = heapArray[current_heap_size - 1];   current_heap_size--;   MinHeapify(0);     return root;   }     // This function deletes key at the   // given index. It first reduced value   // to minus infinite, then calls extractMin()   public void deleteKey(int key) {   decreaseKey(key, Integer.MIN_VALUE);   extractMin();   }     // A recursive method to heapify a subtree   // with the root at given index   // This method assumes that the subtrees   // are already heapified   private void MinHeapify(int key) {   int l = left(key);   int r = right(key);     int smallest = key;   if (l   smallest = l;   }   if (r   smallest = r;   }     if (smallest != key) {   swap(heapArray, key, smallest);   MinHeapify(smallest);   }   }     // Increases value of given key to new_val.   // It is assumed that new_val is greater   // than heapArray[key].   // Heapify from the given key   public void increaseKey(int key, int new_val) {   heapArray[key] = new_val;   MinHeapify(key);   }     // Changes value on a key   public void changeValueOnAKey(int key, int new_val) {   if (heapArray[key] == new_val) {   return;   }   if (heapArray[key]   increaseKey(key, new_val);   } else {   decreaseKey(key, new_val);   }   }  }    // Driver Code  class MinHeapTest {   public static void main(String[] args) {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   System.out.print(h.extractMin() + ' ');   System.out.print(h.getMin() + ' ');     h.decreaseKey(2, 1);   System.out.print(h.getMin());   }  }    // This code is contributed by rishabmalhdijo>

パイソン

# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>>self>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if>

(l   heapArray[l]   {   smallest = l;   }   if (r   heapArray[r]   {   smallest = r;   }     if (smallest != key)   {   Swap(ref heapArray[key],   ref heapArray[smallest]);   MinHeapify(smallest);   }  }    // Increases value of given key to new_val.  // It is assumed that new_val is greater  // than heapArray[key].  // Heapify from the given key  public void increaseKey(int key, int new_val)  {   heapArray[key] = new_val;   MinHeapify(key);  }    // Changes value on a key  public void changeValueOnAKey(int key, int new_val)  {   if (heapArray[key] == new_val)   {   return;   }   if (heapArray[key]   {   increaseKey(key, new_val);   } else  {   decreaseKey(key, new_val);   }  }  }    static class MinHeapTest{    // Driver code  public static void Main(string[] args)  {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);     Console.Write(h.extractMin() + ' ');   Console.Write(h.getMin() + ' ');     h.decreaseKey(2, 1);   Console.Write(h.getMin());  }  }    // This code is contributed by  // Dinesh Clinton Albert(dineshclinton)>

JavaScript

// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && arr[>>this>.parent(i)]>到着[i])>> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>到着[i])>> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest !== i)   {   [arr[i], arr[smallest]] = [arr[smallest], arr[i]]   this.MinHeapify(smallest);   }   }  }    let h = new MinHeap();   h.insert(3);   h.insert(2);   h.deleteKey(1);   h.insert(15);   h.insert(5);   h.insert(4);   h.insert(45);     console.log(h.extractMin() + ' ');   console.log(h.getMin() + ' ');     h.decreaseKey(2, 1);   console.log(h.extractMin());>

Java文字列の文字列

出力

2 4 1>

ヒープの応用:

ヒープソート : ヒープソートはバイナリヒープを使用して、O(nLogn) 時間で配列をソートします。
優先キュー: バイナリヒープを使用すると、O(log N) 時間での insert()、delete() および extractmax()、decreckeyKey() 操作がサポートされるため、優先キューを効率的に実装できます。二項ヒープとフィボナッチヒープは、バイナリヒープのバリエーションです。これらのバリエーションも結合を効率的に実行します。
グラフアルゴリズム: プライオリティキューは、特に次のようなグラフアルゴリズムで使用されます。ディクストラの最短道そして Prim の最小スパニングツリー。
ヒープを使用すると、多くの問題を効率的に解決できます。たとえば、次を参照してください。 a) 配列内の K 番目に大きい要素。 b) ほぼソートされた配列をソート/ c) K 個のソートされた配列をマージする。

関連リンク：

ヒープ上のコーディングの実践
ヒープに関するすべての記事
PriorityQueue : Java ライブラリでのバイナリヒープの実装