私たちは知っています 木 は非線形データ構造です。子供の数に制限はありません。あ完全な二分木とは何ですか?
完全なバイナリ ツリーは、可能な限り左から埋められる最下位レベルのノードを除いて、ツリーのすべてのレベルが完全に埋められる特殊なタイプのバイナリ ツリーです。

完全なバイナリ ツリー
完全なバイナリ ツリーのいくつかの用語:
- 根 – 親からエッジが来ていないノード。例 -ノード A
- 子供 – 何らかの入力エッジを持つノードは子と呼ばれます。例 – ノード B、F はそれぞれ A と C の子です。
- 兄弟 – 同じ親を持つノードは兄弟です。例 - D と E は同じ親 B を持つため兄弟です。
- ノードの次数 – 特定の親の子の数。例 - A の次数は 2、C の次数は 1。D の次数は 0 です。
- 内部/外部ノード – リーフ ノードは外部ノードであり、非リーフ ノードは内部ノードです。
- レベル – 宛先ノードに到達するためのパス内のノードをカウントします。例 - ノード A と B がパスを形成しているため、ノード D のレベルは 2 です。
- 身長 – 宛先ノードに到達するエッジの数。ルートは高さ 0 にあります。 例 – ルートから 2 つのエッジがあるため、ノード E の高さは 2 です。
完全なバイナリ ツリーのプロパティ:
- 完全な二分木は、すべての葉が同じ深さを持つ適切な二分木であると言われます。
- 完全な二分木の深さのノード数 d は 2 d 。
- 完全なバイナリツリーでは、 n ツリーのノードの高さは ログ(n+1) 。
- すべてのレベル 最後のレベルを除いて 完全にいっぱいです。
完璧な二分木 vs 完全なバイナリ ツリー:
最大数のノードを持つ高さ「h」の二分木は、 完璧 二分木。
所定の高さの場合 h 、ノードの最大数は 2 h+1 -1 。
あ 完了 高さ h の二分木は、高さまでの完全な二分木です h-1 、および最後のレベルの要素は左から右の順序で格納されます。
例 1:
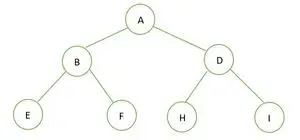
二分木
指定されたバイナリ ツリーの高さは 2 で、そのツリー内のノードの最大数は n= 2 です。h+1-1 = 22+1-1 = 23-1 = 7 。
したがって、次のように結論付けることができます 完璧な二分木 。
さて、完全な二分木ですが、高さまでいっぱいです h-1 つまり; 1、最後のレベルの要素は左から右の順序で格納されます。したがって、これは完全なバイナリ ツリーでもあります。配列に格納されたときの要素の表現は次のとおりです。

配列にレベルごとに格納される要素
配列では、すべての要素が連続的に格納されます。
例 2:
Pythonのソート辞書
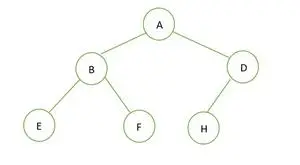
二分木
指定されたバイナリ ツリーの高さは 2 で、存在する必要があるノードの最大数は 2 です。h+1– 1 = 22+1– 1 = 23– 1 = 7 。
しかし、ツリー内のノードの数は 6 。したがって、それは 完璧な二分木ではない 。
さて、完全な二分木ですが、高さまでいっぱいです h-1 つまり; 1 、最後のレベル要素は左から右の順序で格納されます。したがって、これは 完全な二分木 。要素を配列に格納すると、次のようになります。
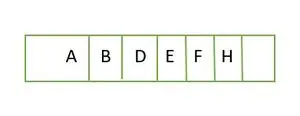
配列にレベルごとに格納される要素
例 3:
機械学習とその型
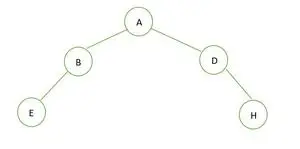
二分木
二分木の高さは 2 で、そこに存在できるノードの最大数は 7 ですが、ノードは 5 つしかないため、 完璧な二分木ではない 。
完全なバイナリ ツリーの場合、最後のレベルでは要素が左から右の順序で埋められていないことがわかります。そうです 完全な二分木ではない 。
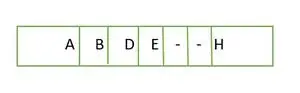
配列にレベルごとに格納される要素
配列内の要素は連続していません。
完全なバイナリ ツリーと完全なバイナリ ツリー:
完全なバイナリ ツリーの場合、すべてのノードには 2 つの子があるか、0 つの子があります。
例 1:
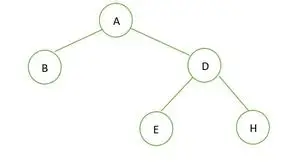
二分木
指定された二分木には次数 1 のノードはなく、各ノードの子が 2 つまたは 0 であるため、次のようになります。 完全なバイナリツリー 。
完全なバイナリ ツリーの場合、要素は最後のレベルの左端からではなく、レベルごとに格納されます。したがって、これは 完全な二分木ではない 。配列表現は次のとおりです。
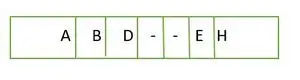
配列にレベルごとに格納される要素
例 2:
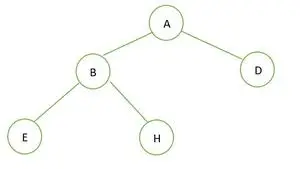
バイナリ ツリー
指定された二分木には次数 1 のノードはありません。すべてのノードは次数 2 または 0 のいずれかを持ちます。 完全なバイナリツリー 。
完全なバイナリ ツリーの場合、要素はレベルごとに格納され、最後のレベルの左端から埋められます。したがって、これは 完全な二分木 。以下はツリーの配列表現です。
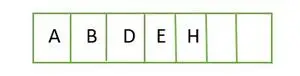
配列にレベルごとに格納される要素
例 3:
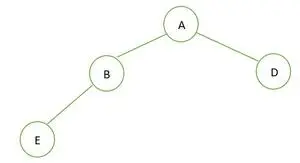
二分木
指定されたバイナリ ツリーでは、ノード B の次数 1 は完全なバイナリ ツリーの特性に違反するため、次のようになります。 完全なバイナリ ツリーではない
Javaリンクリスト
完全なバイナリ ツリーの場合、要素はレベルごとに格納され、最後のレベルの左端から埋められます。したがって、これは 完全な二分木 。バイナリ ツリーの配列表現は次のとおりです。
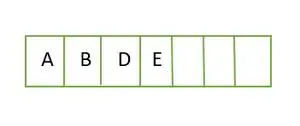
配列にレベルごとに格納される要素
例 4:
平均と平均
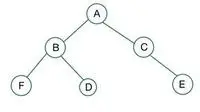
二分木
指定されたバイナリ ツリーでは、ノード C の次数 1 は完全なバイナリ ツリーのプロパティに違反するため、次のようになります。 完全なバイナリ ツリーではない
完全なバイナリ ツリーの場合、要素はレベルごとに格納され、最後のレベルの左端から埋められます。ここでノード E は条件に違反します。したがって、これは 完全な二分木ではない 。
完全なバイナリ ツリーの作成:
私たちは知っています 完全な二分木 は、最後のレベルを除いて次のようなツリーです (たとえば、 私 )他のすべてのレベルには ( 2リットル ) のノードがあり、左側から右側にノードが並んでいます。
配列を使用して表現できます。親がインデックスの場合 私 左側の子は 2i+1 そして右の子は 2i+2 。
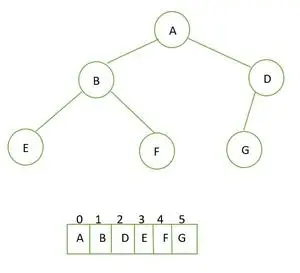
完全なバイナリ ツリーとその配列表現
アルゴリズム:
の作成のために 完全なバイナリ ツリー が必要です。 ステップ1: ツリーが空の場合は、ルートを新しいノードで初期化します。
ステップ2: ツリーが空でない場合は、フロント要素を取得します
- フロント要素に左の子がない場合は、左の子を新しいノードに設定します。
- 正しい子が存在しない場合は、正しい子を新しいノードとして設定します
ステップ 3: ノードに両方の子がある場合、 ポップ キューからです。
ステップ 4: 新しいデータをキューに入れます。
図:
ジャバ8
以下の配列を考えてみましょう。
1. 最初の要素がルートになります (インデックスの値 = 0 )
A がルートとして取得されます
2. 次の要素 (インデックス = にあります) 1 ) が左になり、3 番目の要素 (index = 2 ) ルートの右の子になります
B は左の子、D は右の子
3. 4 番目 (インデックス = 3 ) と 5 番目の要素 (index = 4 ) B ノードの左右の子になります。
E と F は B の左右の子です
4. 次の要素 (インデックス = 5 ) はノード D の左の子になります。
G は D ノードの左の子になります
これにより、完全なバイナリ ツリーが作成されます。
実装: レベル順序トラバーサルから完全なバイナリ ツリーを構築する実装については、次のとおりです。 この郵便受け 。
完全なバイナリ ツリーの適用:
- ヒープソート
- ヒープソートベースのデータ構造
指定されたバイナリ ツリーが完全かどうかを確認します。 フォローする この郵便受け 指定されたバイナリ ツリーが完全かどうかを確認します。




