組み合わせ論理回路は、さまざまなタイプの論理ゲートを含む回路です。簡単に言うと、異なる種類の論理ゲートを組み合わせた回路を「 組み合わせ論理回路 。組み合わせ回路の出力は、前の入力に関係なく、現在の入力の組み合わせから決定されます。入力変数、論理ゲート、および出力変数は、組み合わせ論理回路の基本コンポーネントです。組み合わせ論理回路には、加算器、減算器、デコーダ、エンコーダ、マルチプレクサ、デマルチプレクサなど、さまざまなタイプがあります。
組み合わせ論理回路には次のような特徴があります。
- いかなる瞬間においても、組み合わせ回路の出力は現在の入力端子にのみ依存します。
- 組み合わせ回路にはバックアップや以前のメモリがありません。回路の現在の状態は、入力の前の状態の影響を受けません。
- 組み合わせ論理回路では、n 個の入力と m 個の出力が可能です。
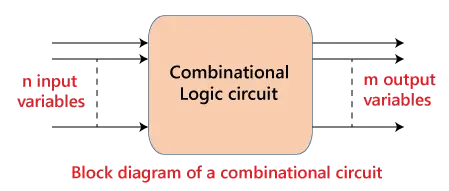
「n」入力変数は外部ソースから取得され、「m」出力変数は外部宛先に送られます。多くのアプリケーションでは、ソースまたは宛先はストレージ レジスタです。
半加算器
半加算器は、2 つの入力と 2 つの出力を持つ基本的な構成要素です。加算器は、2 つの単一ビット 2 進数の OR 演算を実行するために使用されます。の 運ぶ そして 和 は半加算器の 2 つの出力状態です。
全加算器
半加算器は 2 つの数値のみを加算するために使用されます。この問題を克服するために、全加算器が開発されました。全加算器は、3 つの 1 ビット 2 進数 A、B、およびキャリー C を加算するために使用されます。全加算器には、3 つの入力状態と 2 つの出力状態 (合計とキャリー) があります。
半減算器
半減算器も、2 つの 2 進数を減算する構成要素です。 2 つの入力と 2 つの出力があります。この回路は、2 つの単一ビット 2 進数 A と B を減算するために使用されます。 '違います ' そして '借りる' は半加算器の 2 つの出力状態です。
完全な減算器
Half Subtractor は、2 つの数値のみを減算するために使用されます。この問題を克服するために、フル減算器が設計されました。フル減算器は、3 つの 1 ビット数値 A、B、C を減算するために使用されます。 減少する、差し引く 、 そして 借りる、 それぞれ。フル減算器には 3 つの入力状態と 2 つの出力状態 (diff とborrow) があります。
マルチプレクサ
マルチプレクサは、n 個のデータ入力と 1 つの出力を持つ組み合わせ回路です。としても知られています データセレクター これにより、入力から 1 つの入力が選択され、それが出力にルーティングされます。選択された入力を利用して、n 個の入力ラインから 1 つの入力ラインが選択されます。イネーブル入力は E で示され、カスケードで使用されます。
デマルチプレクサ
デマルチプレクサは、マルチプレクサの逆の動作を実行します。デマルチプレクサには入力が 1 つだけあり、それが複数の出力に分散されます。ラインを選択することにより、一度に 1 つの出力ラインが選択されます。入力は選択された出力ラインに送信されます。
デコーダ
デコーダは、n 個の入力と最大 m = 2n 個の出力を持つ組み合わせ回路です。デコーダはデマルチプレクサと同じです。デマルチプレクサとデコーダの唯一の違いは、デコーダにはデータ入力がないことです。デコーダは、エンコーダとはまったく逆の動作を実行します。
エンコーダ
エンコーダは、デコーダの逆の操作を実行するために使用されます。 n 個の入力と m 個の出力を持つエンコーダを使用して、デジタル入力番号に関連する m ビットのバイナリ コードを生成します。エンコーダはデジタル ワードを取得し、それを別のデジタル ワードに変換します。
