複利 - 計算式、定義、例 - 算術

複利とは、ローンまたは預金の金額に対して計算される利息で、元金と以前に得られた利息に対して利息が計算されます。

複利と単利の共通の違いは次のとおりです。複利、単利は投資された元本のみに依存するのに対し、利子は元金と以前に受け取った利息に対して計算されます。

複利とは何ですか?
複利計算式
複利の計算方法は?
複利計算式 – 導出
半年複利計算式
四半期複利計算式
毎月の複利計算式
毎日の複利計算式
周期複利計算式
72 のルール
連続複利
連続複利計算式
複利の他の応用例
複利と単利の違い
複利の例
複利 - 練習問題

複利とは何ですか?

複利とは、元本に対する利息と、元本に対して得られる利息のことです。 複利という言葉は 2 つの単語で構成されています コンパウンドとは2つ以上から構成されることを意味し、利子は金額を貸したときに得られるお金を意味します。 したがって、複利は融資によって得られるお金であり、次の 2 種類の利子で構成されます。

元金に対する利息
期間中の元金に対する利息

複利の定義

複利元金と以前に得た利息に基づいて計算される利息です。それはC.I.によって示されます。投資やローンの返済に非常に役立ちます。利子に対する利息とも呼ばれます。

Python Rストリップ

複利は銀行や金融部門で非常に役立ちますが、他の部門でも役立ちます。その用途のいくつかは次のとおりです。

国の人口の増加
一定期間にわたる投資の価値。
あらゆる品物の膨らんだコストと減価償却額を見つけるため。
あらゆる機関や国の成長を予測するために。

複利 (C.I) = 金額 – 元本

複利計算式

複利は、金利と当初元本に基づいて一定期間の総額を計算した後、計算されます。初期元本 P、年利率 r、期間 t (年)、利子の年間複利回数 n の場合、CI の計算式は次のとおりです。

CI = P(1 + r/100) ⁿ –P

上記の複利計算式は、以下の画像形式で追加されます。

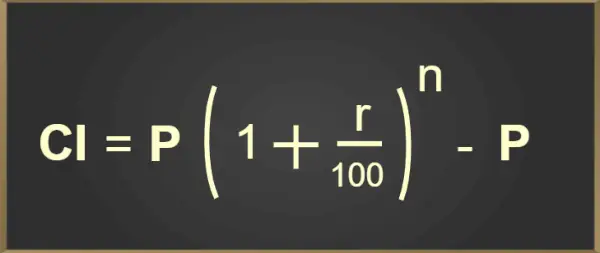
複利計算式

どこ、

P = メイン
r = 金利
n = 年間の利子の複利回数
t = 時間 (年単位)

複利の式は次のように書くことができます。

複利 = A – P

どこ、

あ = 複利後の合計金額
P = 当初元本金額

複利 = P(1 + r/n) ^nt -P

どこ、

P = 当初元本金額
r = 年利率
n = 利息が複利される回数
t = 年数

複利は、要件に応じて、年、半年、四半期、月、日などで計算できます。

複利の計算方法は?

複利元金と累積利息の両方に支払われる利息です。各間隔で得られる利息が最初の元本に追加されるため、元本は増加し続けます。

複利を見つけるには、次の方法を使用します。

ステップ1： ノート、元本、レート、および指定された期間

ステップ 2: 式 A = P(1 + r/100) を使用して量を計算します。 ⁿ

ステップ 3: 式 CI = 金額 – 元本を使用して複利を計算します。

一定の間隔で、それまでに蓄積された利息が現在の元金とクラブ化され、利息が支払われます。 新しいプリンシパルに対して計算される 。新しい元本は、当初の元本とそれまでに蓄積された利息の合計に等しくなります。

複利＝元金利息＋元金利息（2年目以降）

複利は、毎年（毎年）、半年、四半期、毎月などの定期的な間隔で計算されます。 等;投資から得た利息を再投資すると、時間の経過とともにお金の増加が早くなるようなものです。それはまさにお金に対する複利の作用です。 銀行または金融機関は、複利のみに基づいて金額を計算します。

複利計算式 – 導出

複利計算式は、最初の元金に対して獲得または支払われる利息を計算するために金融で使用される強力なツールです。 これには、当初の元本と前の期間に累積された利息の両方が含まれます。複利の計算式は次のようになります。

$A = P left(1 + frac{r}{n} ight)^{nt}$

どこ、

A は利息を含む投資または融資の将来価値です。
Pは元本金額（初期投資額または融資額）
r は年利率 (小数として)
n は、利息が年間に複利計算される回数です。
お金が投資または借りられる期間です（年単位）

単利計算式

単利は元金のみで計算されます。 という式で表すことができます 、

A = P + P cdot r cdot t

連続複利による複利計算式

利息が継続的に複利計算される場合 (年に無制限に)、複利の計算式は連続複利計算の公式を使用して導出されます。

$A = P cdot e^{rt}$

どこ、

e はオイラー数 (約 2.71828)
P は元本金額
rは年利率です
年単位の時間です

一般的な複利計算式

一般的な複利計算式を導き出すために、1 年に n 回複利が発生することを考えてみましょう。

もし P は年利 r で年に n 回複利計算され、利子 r を n で割って年に n 回適用されます。したがって、t 年後、式は次のようになります。

$A = P left(1 + frac{r}{n} ight)^{nt}$

どこ、

$frac{r}{n}$ 複利期間あたりの金利を表します。
nt は、t 年間にわたる複利期間の合計数です。

これ 式は、利息が一定の間隔で複利になった場合に、時間の経過とともに最初の元金がどのように増加するかを示しています 。 n が無限大に近づくにつれて (つまり、連続複利)、式は連続複利の公式に向かって収束します。 $A = P cdot e^{rt}$ 。

要約すれば、 複利の計算式 $A = P left(1 + frac{r}{n} ight)^{nt}$ これは、年間の個別の配合期間に適応した連続配合配合の結果です。 定期的な複利を考慮して、投資またはローンの将来価値を計算できます。

半年複利計算式

投資元本を P、利率を年 R % とします。これは「t」年間、半年ごとに複利計算されます。

として 半年複利で6ヶ月の終わりに元金が変わります、 それまでに得た利息が元金に加算され、それが新しい元金となります。同様に、最終的な金額が計算されます。

私たちは知っています、

レート = 年間複利半年あたり R%

率 = (R/2) %

時間は t 年です。t 年が経過していることはわかっています。 2t 半年。

今、

A = P (1 + R/200) ^2t

CI = A – P

四半期複利計算式

投資元本を P、利率を年 R % とし、t 年間四半期ごとに複利計算します。

として 四半期ごとに複利計算され、3 か月後に元本が変更されます。 そして それまでに得た利息が元金に加算され、それが新しい元金となります。同様に、最終的な金額が計算されます。

私たちは知っています、

レート = 四半期複利の年率 R%

率 = (R/4)%

時間は t 年です。t 年が経過していることはわかっています。 4t 四分の一。

今、

A = P(1 + R/400) ^4t

CI = A – P

チェック： 四半期複利計算式

毎月の複利計算式

毎月複利の場合、複利回数は12回となり、毎月の利息は年複利の12分の1となります。 したがって、月次複利計算式は次のようになります。

A = P[1 + (R/1200)] ^12t

CI = A – P

チェック： 毎月の複利計算式

毎日の複利計算式

利息が毎日複利になる場合は、

新しい金利は R/365 % になります

java intをdoubleにする

n = 365

したがって、毎日の複利計算式は次のように与えられます。

A = P[1 + (R/36500)] ^365t

CI = A – P

周期複利計算式

元本 P と複利 CI を含む合計金額は、次の式で求められます。

A = P[1 + (r/n)] ^nt

どこ、

P = メイン
A = 最終金額
r = 年利率
n = 利息が複利になる回数
t = 時間 (年単位)

したがって、複利は次のようになります。

CI = A – P

72 のルール

72 の法則は、毎年複利で運用した場合に、私たちのお金が何年で 2 倍になるかを見積もるために使用される公式です。 のために例、私たちのお金が投資されている場合 r% 毎年複利計算すると、私たちのお金が2倍になるまでに72/r年かかります。

この計算は、膨らんだお金の価値を計算するのにも役立ちます。 つまり、資産が毎年減価償却される場合、その価値が何年で半減するかを示します。

72 の法則の公式

次の式は、投資が 2 倍になるまでの年数を概算するために使用されます。

N = 72 / r

どこ、

N これは私たちのお金が2倍になるおおよその年数です
r 私たちのお金が毎年複利計算されるレートです

72 の法則の例

カビール氏が 8% の収益をもたらす負債ファンドに 1,000,000 ルピーを投資したとします。 毎年複利で運用した場合、そのお金が何年で2倍になるかを求めてください。

上の式を使用すると、N = 72/8 = 9 年となります。

したがって、 カビール氏の資産が2倍になるには9年かかる。

連続複利

同じ金額、同じ金利の場合。 C.I.特定の年の C.I は常に前年の C.I よりも大きくなります。 (3 年目の CI は 2 年目の CI よりも大きい)。 連続する 2 年間の CI の差額は、前年の C.I に対する 1 年間の利息となります。

3年目のC.I – 2年目のC.I = 2年目のC.I × r × 1/100
JavaScript グローバル変数

連続する 2 年間の金額の差は、前年の金額に対する 1 年間の利息となります。

3年目金額 – 2年目金額 = 2年目金額 × r × 1/100

主な結果

同じ金額、同じレートの場合 、

n 年目の C.I = (n – 1) 年目の C.I + (n – 1) 年目の C.I の 1 年間の利息

連続複利計算式

連続複利式は、さまざまな期間にわたって継続的に複利計算が行われ、時間の経過とともに価値が追加される投資の最終価値を計算するために財務で使用されます。連続配合の式は次のようになります。

最終価値 = 現在価値 × e ^RT

どこ、

rは金利です
時間です

もっと詳しく知る、 連続配合フォーミュラ

複利の他の応用例

成長： これは主に、業界が関連している場合の成長のために使用されます。

n 年後の生産量 = 初期生産量 × (1 + r/100) ⁿ

減価償却: 製品のコストが毎年 r% ずつ減価すると、n 年後のその価値は次のようになります。

現在価値 × (1 + r/100) ⁿ

人口問題: 町、市、または村の人口が毎年一定の割合で増加する場合。

n年後の人口 = 現在の人口 × (1 + r/100) ⁿ

複利と単利の違い

複利と単利の違いについては、この記事で詳しく説明しています。

複利と単利
複利 (CI)	単利（SI）
CI は、元本と以前に得られた利息の両方に基づいて計算される利息です。	SI は元本のみに基づいて計算される利息です。
同じ原則、料金、期間の場合 CI> はい	同じ原則、料金、期間の場合うん
CI の計算式は次のとおりです。 A = P(1 + R/100) T CI = A – P	SI の式は次のとおりです。 IF = (P×R×T) / 100

複利の例

複利計算式の例としては、次のようなものがあります。

例 1: 元本 = Rs 6000、金利 = 年率 10%、期間 = 2 年の場合の複利を求めます。

解決：

初年度の利息 = (6000 × 10 × 1)/100 = 600

1 年目の年度末の金額 = 6000 + 600 = 6600

2 年目の利息 = (6600 × 10 × 1) / 100 = 660

2 年目の年末の金額 = 6600 + 660 = 7260

複利 = 7260 – 6000 = 1260

例 2: 金利が年 2% の場合、2 年間で 8000 ルピーの複利はいくらになりますか?

解決：

考えると、

メインP = 8000
率 r = 2%
時間 = 2 年
式で

A = P (1 + R/100) ⁿ

A = 8000 (1 + 2/100)²= 8000 (102/100)²

A = 8323

複利 = A – P = 8323 – 8000 = Rs 323

例 3: Hari は Rs を入金しました。金融会社に 4000 ドルを 2 年間、年利 5% で貸し付けます。 Rohit が 2 年後に得られる複利はいくらですか?

解決：

考えると、

メインP = 4000
率 r = 5%
時間 = 2 年
式で表すと、

A = P (1 + R/100)ⁿ

A= 4000 (1 + 5/100)²

A= 4000 (105/100)²

A=4410

複利 = A – P = 4410 – 4000 = 410

例 4: Rs の複利を求めます。 2000 年から 1.5 年間、年率 4% で適用されます。半年複利の場合は？

解決：

考えると、

メイン p = 2000
率 r = 4%
時間 = 1.5 (つまり 3 半年)
式により、

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

複利 = A – P = 2122 – 2000 = 122
監督カラン・ジョーハル

例 5: 四半期ごとに複利計算される場合、年率 20% で 1 年間の 10000 の複利はいくらですか?

解決：

考えると、

元金 P = Rs 10000
レート R = 12% (12/4 = 四半期ごとに 3 %)
時間 = 1 年 (1 × 4 = 4 四半期)
式によりますと、

A = P (1 + R/100) ⁿ

A = 10000 (1 + 3/100) ⁴

A = 10000 (103/100) ⁴

A = 11255

複利 = A – P = 11255 – 10000 = 1255

例 6: 元金に対して 2 年間、年率 5% の複利を求めます。これは、2 年間で Rs が与えられた場合、年率 5% になります。単利として400円。

解決：

考えると、

単利 IF = 400
レート R = 5%
時間 T = 2 年
式によりますと、

単利 = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 複利率 = 5%

P = 40000/10 = 4000 ルピー

時間 = 2 年

式によりますと、

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

複利 = A – P = 4410 – 4000 = 410

例 7: Rs 30000 に対して、2 年間毎年 7% の複利で複利を計算します。

解決：

元金 P = Rs 30000
レート R = 7%
時間 = 2 年
式で表すと、

A = P (1 + R/100) ⁿ

A = 30000 (1 + 7/100) ²

A = 30000 (107/100) ²

A = 34347

複利 = A – P = 34347 – 30000 = 4347
Javaの正規表現

関連記事:

毎日の複利
毎月の複利
クラス 8 複利ソリューション
複利 – 適性に関する質問と回答
単利

複利 - 練習問題

複利に関するさまざまな練習問題は、

Q1.合計 10,000 を年複利 4% で貸した場合、3 年後に支払わなければならない金額を求めます。

Q2.合計 2500 を半年複利 6% で貸した場合、1.5 年後に利息を支払う必要があることを求めます。

Q3. 9,000 円を 15 か月間四半期ごとに 5% の金利で貸与した場合の複利を計算します。

Q4. 20,000 円を 12% の金利で 3 か月間毎月複利で貸与した場合の複利を計算します。

複利の結論

複利というのは、 投資や融資を時間の経過とともに拡大または蓄積できる強力な財務概念。 とは異なり 単利は最初の元金に対してのみ利息を計算します。 複利 当初の元本と過去の期間からの累積利息の両方に対して得られる利息が考慮されます。

複利 – よくある質問

複利とはどういう意味ですか?

複利とは、元金と一定期間に得られた前回の利息に基づいて計算される利息です。

複利の計算方法は?

複利を計算するには、最初に最終金額が計算され、それから元本から差し引かれて最終的な複利が得られます。金額は次の式を使用して計算されます。

A = P(1 + R/100) ^t

CI = A – P

投資家にとって複利は単利よりも優れているのでしょうか?

はい、投資家にとって複利は単利よりもはるかに優れています。

毎日複利計算する場合、複利計算式とは何ですか?

指定された元本が P、金利が R、期間が T 年であると仮定すると、毎日複利計算される場合の複利計算式は次のようになります。

A = P(1 + R/365) ^{365×T}

CIとSIの違いは何ですか?

CI と SI の基本的な違いは、SI は元本金額に請求される利息であるのに対し、CI は元本金額および元金に累積された利息に請求される利息であることです。