あ カウンター 特定のイベントまたはプロセスが発生した回数を、多くの場合クロック信号に関連して保存 (場合によっては表示) するデバイスです。カウンタはデジタル電子機器でカウントの目的で使用され、回路内で発生する特定のイベントをカウントできます。たとえば、UP カウンタでは、カウンタはクロックの立ち上がりエッジごとにカウントを増加します。カウントするだけでなく、カウンタはランダム シーケンス 0、1、3、2… など、設計に基づいて特定のシーケンスに従うことができます。また、フリップフロップを使用して設計することもできます。これらは、与えられたパルス波形の周波数を分周する分周器として使用されます。カウンタは、パルスの数をバイナリ コードまたは BCD 形式でカウントする順序回路です。カウンタの主なプロパティは、タイミング、シーケンス、およびカウントです。カウンターは 2 つのモードで動作します
アップカウンター
ダウンカウンター
カウンタの分類
カウンターは大きく2つに分類される
- 非同期カウンタ
- 同期カウンタ
1. 非同期カウンタ
非同期カウンタではユニバーサル クロックを使用せず、最初のフリップ フロップのみがメイン クロックによって駆動され、後続のフリップ フロップの残りのクロック入力は前のフリップ フロップの出力によって駆動されます。次の図で理解できます。
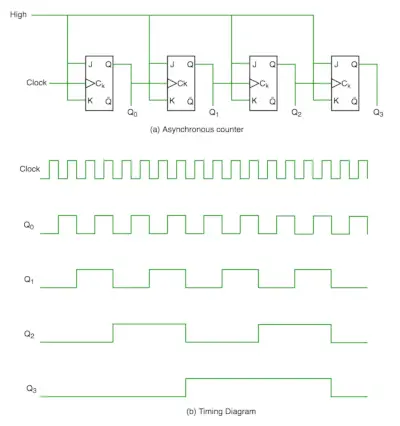
タイミング図から明らかなように、クロック パルスの立ち上がりエッジに遭遇するとすぐに Q0 が変化し、Q0 の立ち上がりエッジに遭遇すると Q1 が変化します (Q0 は 2 番目のフリップフロップのクロック パルスに似ているため)。このようにリップルは Q0、Q1、Q2、Q3 を通じて生成されるため、このとも呼ばれます。 リップルカウンターとシリアルカウンター。 リップル カウンタはフリップ フロップをカスケード接続したもので、1 つのフリップ フロップの出力が次のフリップ フロップのクロック入力を駆動します。
2. 同期カウンタ
非同期カウンタとは異なり、同期カウンタには各フリップフロップを駆動する 1 つのグローバル クロックがあり、出力が並行して変化します。同期カウンタの非同期カウンタに対する利点の 1 つは、各フリップフロップに同じクロックが与えられるため累積遅延が発生しないため、非同期カウンタよりも高い周波数で動作できることです。パラレルカウンタとも呼ばれます。
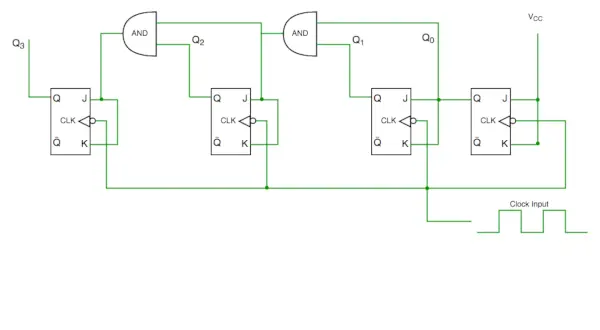
同期カウンタ回路
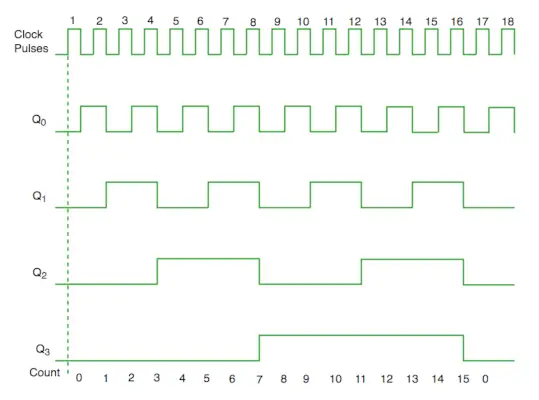
タイミング図 同期カウンタ
回路図から、Q0 ビットがクロックの各立ち下がりエッジに応答する一方、Q1 は Q0 に依存し、Q2 は Q1 と Q0 に依存し、Q3 は Q2、Q1、および Q0 に依存することがわかります。
ディケイドカウンター
ディケイド カウンタは 10 の異なる状態をカウントし、その後初期状態にリセットされます。単純な 10 年カウンターは 0 から 9 までカウントしますが、0 から 15 までの任意の 10 状態を通過できる 10 年カウンターを作成することもできます (4 ビットカウンターの場合)。
| クロックパルス | Q3 | 第2四半期 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
シンプルな10年カウンタの真理値表
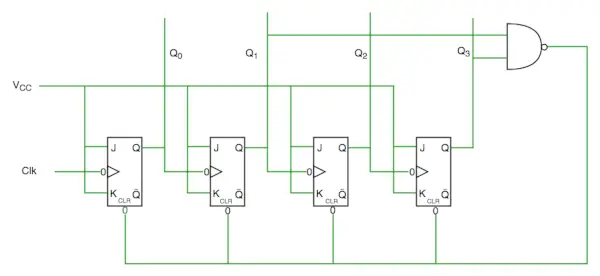
ディケイドカウンター回路図
回路図から、Q3 と Q1 に Nand ゲートを使用し、これをクリア入力ラインに供給していることがわかります。10 の 2 進表現は次のとおりです。
1010
ここで Q3 と Q1 が 1 であることがわかります。これら 2 ビットの NAND をクリア入力に与えると、カウンタは 10 でクリアされ、再び最初から開始されます。
大事なポイント : カウンタで使用されるフリップフロップの数は常に ( ログ2n ) ここで、n = カウンタ内の状態の数。
過去数回のカウンターでのゲート質問
Q1.以下に示すように、シーケンス 0-2-3-1-0 に従う T フリップフロップを使用した 2 ビット カウンターの部分的な実装を考えてみましょう。
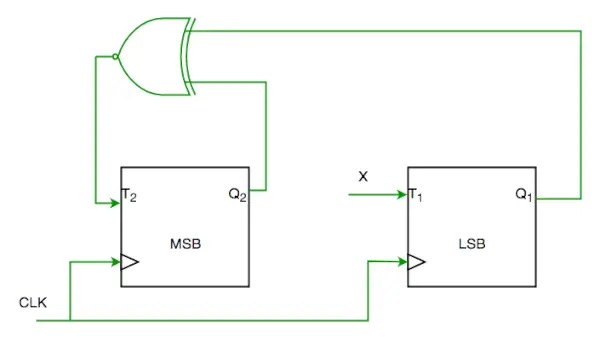
回路を完成させるには、入力 X は次のようにする必要があります。
(答)Q2?
(B) 第 2 問 + 第 1 問
(C) (Q1 ? Q2)』
(D) Q1?第2四半期 (ゲート-CS-2004)
解決:
回路から見ると
T1=XQ1’+X’Q1—-(1)
そして
T2=(Q2 ? Q1)’—-(2)
必要な出力は 00->10->11->01->00 です
したがって、X はこうあるべきです Q1Q2'+Q1'Q2 1と2を満たしています。
つまり、ANS は (D) パートです。
Q2. 4 ビット バイナリカウンタの制御信号の機能は次のとおりです (X はドントケアです)。
カウンタは次のように接続されます。
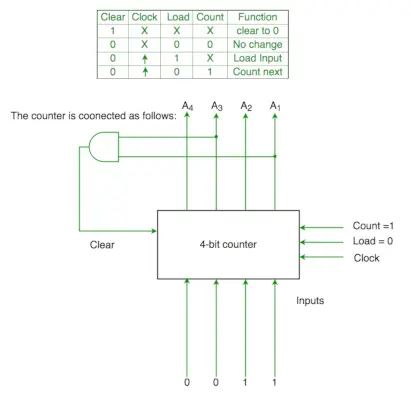
カウンタとゲートの遅延は無視できるものと仮定します。カウンタが 0 から始まる場合、次のシーケンスを繰り返します。
(A) 0、3、4
(B) 0、3、4、5
(C) 0、1、2、3、4
(D) 0、1、2、3、4、5 (ゲート-CS-2007)
解決:
最初は A1 A2 A3 A4 =0000
Clr=A1 および A3
したがって、A1 と A3 が両方とも 1 の場合、再び 0000 になります。
したがって、0000(初期) -> 0001(A1 および A3=0) -> 0010 (A1 および A3=0) -> 0011(A1 および A3=0) -> 0100 ( A1 と A3=1 )[クリア条件を満たした] ->0000(init.) なので、0->1->2->3->4 となります。
答えは(C)の部分です。
トジソン・ジャワ
デジタルロジックに関するクイズ
アヌジ・バタム氏による寄稿記事
