DFA と NFA の違い - TECHCODEVIEW.COM

1. DFA: DFA は決定論的有限オートマトンを指します。有限オートマトン (FA) は、入力シンボルに対応し、結果として生じる状態が 1 つだけ、つまり遷移が 1 つだけ存在する場合、決定的であると言われます。決定論的有限オートマトンは、次のように表される 5 つのタプルのセットです。

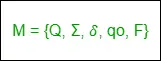
どこ、
Q: 有限制御内の空でない有限の状態セット(qo、q1、q2、…)。
Σ: 入力シンボルの空でない有限セット。
δ: これは、状態と入力シンボルの 2 つの引数を受け取り、単一の状態を返す遷移関数です。
qo: 開始状態であり、Q の状態の 1 つです。
F: これは、Q に属するセットからの最終状態/受け入れ状態の空ではないセットです。

2. 原因:
NFA は非決定性有限オートマトンを指します。有限オートマトン (FA) は、同じ入力シンボル上で 1 つの状態から複数の可能な遷移がある場合、非決定的であると言われます。
非決定性有限オートマトンも 5 つのタプルのセットであり、次のように表されます。

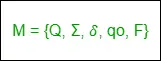
どこ、
Q: 空ではない有限状態のセット。
Σ: 空ではない有限入力シンボルのセット。
δ: Q から状態と入力シンボルを取得し、Q のサブセットを返す遷移関数です。
qo: NFA の初期状態と Q のメンバー。
F: 最終状態の空でないセットおよび Q のメンバー。

前提条件 – 完成した自動

DFA と NFA の違い:

DFA	NFA
DFA は Deterministic Finite Automata の略です。	NFA は Nondeterministic Finite Automata の略です。
アルファベットの各記号表現に対して、DFA には状態遷移が 1 つだけ存在します。	NFA が何らかのシンボルに従ってどのように反応するかを指定する必要はありません。
DFA は空の文字列トランジションを使用できません。	NFA は空の文字列遷移を使用できます。
DFA は 1 つのマシンとして理解できます。	NFA は、複数の小さなマシンが同時にコンピューティングするものとして理解できます。
DFA では、次に考えられる状態が明確に設定されます。	NFA では、状態と入力シンボルの各ペアは、多くの可能な次の状態を持つことができます。
DFA は構築がより困難です。	NFA の構築は簡単です。
DFA は、受け入れ状態とは異なる状態で文字列が終了した場合、文字列を拒否します。	すべてのブランチが停止するか文字列を拒否した場合、NFA は文字列を拒否します。
入力文字列の実行に必要な時間が短縮されます。	入力文字列の実行に必要な時間が長くなります。
すべての DFA は NFA です。	すべての NFA が DFA であるわけではありません。
DFA にはさらに多くのスペースが必要です。	NFA は DFA よりも少ないスペースを必要とします。
デッド構成は許可されません。例: q0 状態で入力を 0 として与える場合、自己ループとして q0 への入力として 1 を与える必要があります。	デッド構成は許可されます。例: q0 ステートで入力 0 を与えると、q1 で次の入力 1 を与えることができ、次のステートに進みます。
δ: QxΣ -> Q、つまり、次に考えられる状態は Q に属します。	δ: Qx(Σ U ε) -> 2^Q つまり、次に考えられる状態は Q の累乗集合に属します。
DFA ではバックトラックが許可されています。	NFA ではバックトラッキングが常に可能であるとは限りません。
正規表現を DFA に変換するのは困難です。	正規表現から NFA への変換は、DFA に比べて簡単です。
イプシロン移動は DFA では許可されません	NFAではイプシロン移動が許可されています
DFA では、単一の入力アルファベットに対して 1 つの移動のみが許可されます。	単一の入力アルファベットに対して選択 (複数の移動) が可能です。