エンコーダは、一連のバイナリ入力を固有のバイナリ コードに変換するデジタル回路です。バイナリ コードは入力の位置を表し、アクティブな特定の入力を識別するために使用されます。エンコーダは、パラレル入力セットをシリアル コードに変換するためにデジタル システムで一般的に使用されます。
エンコーダの基本原理は、考えられる各入力に一意のバイナリ コードを割り当てることです。たとえば、2 対 4 ライン エンコーダには 2 つの入力ラインと 4 つの出力ラインがあり、2^2 = 4 つの可能な入力の組み合わせのそれぞれに一意の 4 ビット バイナリ コードを割り当てます。エンコーダの出力は通常、アクティブ ローです。これは、常に 1 つの出力だけがアクティブ (ロー) で、残りの出力は非アクティブ (ハイ) であることを意味します。アクティブ ロー出力は、アクティブ入力に割り当てられたバイナリ コードに基づいて選択されます。
エンコーダには、各入力に優先順位を割り当てるプライオリティ エンコーダや、バイナリ重み付けシステムを使用して入力にバイナリ コードを割り当てるバイナリ重み付けエンコーダなど、さまざまなタイプがあります。要約すると、エンコーダは、一連のバイナリ入力を、入力の位置を表す固有のバイナリ コードに変換するデジタル回路です。エンコーダは、パラレル入力をシリアル コードに変換するためにデジタル システムで広く使用されています。
エンコーダーとは、 組み合わせ回路 の逆の操作を実行します。 デコーダ 。最大値は次のとおりです 2^n 入力行 そして 「n」出力行 したがって、2^n 入力からの情報を n ビット コードにエンコードします。アクティブ High の入力と同等のバイナリ コードを生成します。したがって、エンコーダは 2^n 入力ラインを「n」ビットでエンコードします。
エンコーダ
ubuntuビルド必須
エンコーダの種類
エンコーダにはさまざまなタイプがありますが、それらについては以下で説明します。
- 4対2エンコーダ
- 8 進数から 2 進数へのエンコーダー (8 対 3 エンコーダー)
- 10 進数から BCD へのエンコーダ
- プライオリティエンコーダ
4対2エンコーダ
4 to 2 エンコーダは次のもので構成されます。 4 つの入力 Y3、Y2、Y1、Y0、および 2 つの出力 A1、A0 。出力でそれぞれのバイナリ コードを取得するには、常にこれら 4 つの入力のうち 1 つだけを「1」にすることができます。以下の図は、4 to 2 エンコーダの論理シンボルを示しています。
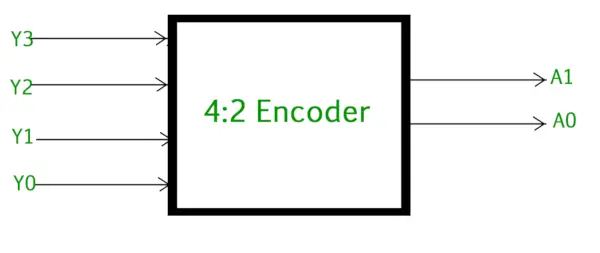
4対2エンコーダ
4 to 2 エンコーダの真理値表は次のとおりです。
| 入力 | 出力 | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
A1 と A0 の論理式:
A1 = Y3 + Y2 A0 = Y3 + Y1>
上記の 2 つのブール関数 A1 および A0 は、2 つの入力 OR ゲートを使用して実装できます。
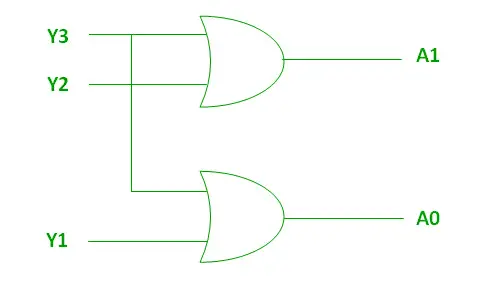
ORゲートを使用した実装
8 進数から 2 進数へのエンコーダー (8 対 3 エンコーダー)
8 to 3 エンコーダーまたは 8 進数から 2 進数へのエンコーダーは、次のもので構成されます。 8入力 :Y7~Y0および 3出力 :A2、A1、A0。各入力ラインは各 8 進数に対応し、3 つの出力は対応するバイナリ コードを生成します。以下の図は、8 進数から 2 進数のエンコーダーへの論理シンボルを示しています。
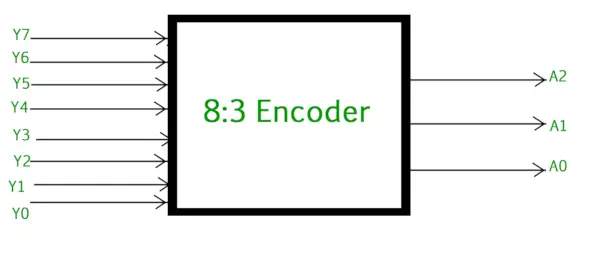
8 進数から 2 進数へのエンコーダー (8 対 3 エンコーダー)
8 to 3 エンコーダの真理値表は次のとおりです。
| 入力 | 出力 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
A2、A1、および A0 の論理式。
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
上記の 2 つのブール関数 A2、A1、および A0 は、4 つの入力を使用して実装できます。 OR ゲート 。
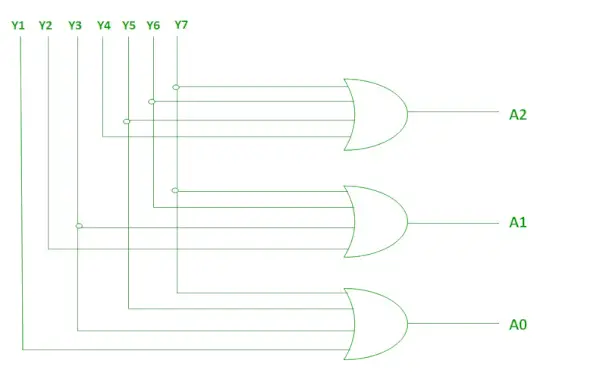
ORゲートを使用した実装
10 進数から BCD へのエンコーダ
10 進数から 2 進数へのエンコーダーは通常、次のもので構成されます。 10入力ライン そして 4つの出力ライン 。各入力ラインは各 10 進数字に対応し、4 つの出力は BCD コードに対応します。このエンコーダは、デコードされた 10 進データを入力として受け入れ、それを出力ラインで使用できる BCD 出力にエンコードします。以下の図は、10 進数から BCD へのエンコーダの論理シンボルを示しています。
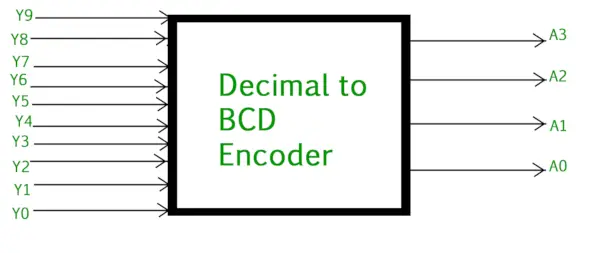
10 進数から BCD へのエンコーダ
10 進数の真理値表 BCDエンコーダ 以下のとおりであります。
| 入力 | 出力 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | Y8 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
A3、A2、A1、および A0 の論理式。
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
上記の 2 つのブール関数は、OR ゲートを使用して実装できます。
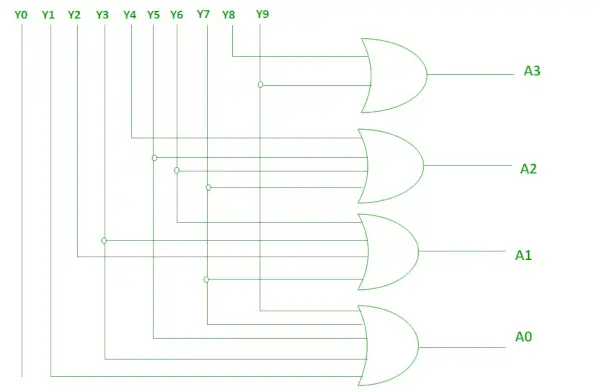
ORゲートを使用した実装
プライオリティエンコーダ
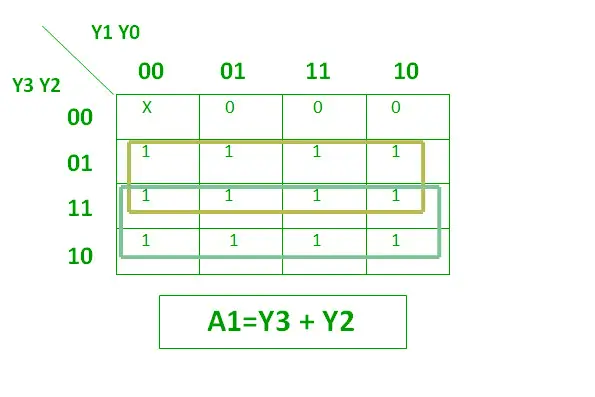
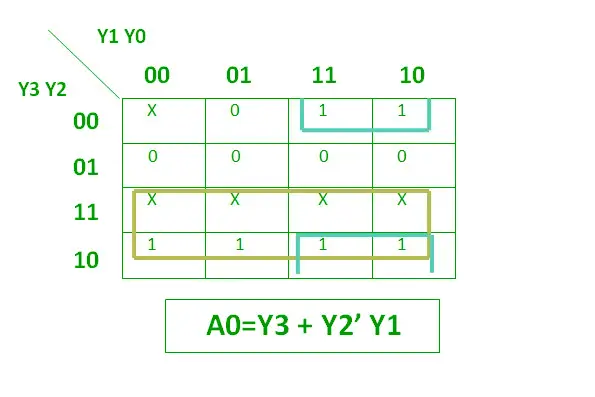
4 対 2 プライオリティ エンコーダには、 4入力 : Y3、Y2、Y1、Y0、および 2出力 :A1とA0。ここで、入力 Y3 には、 最優先 、一方、入力 Y0 には 最も優先度が低い 。この場合、複数の入力が同時に「1」であっても、出力は入力に対応する(バイナリ)コードになります。 優先度が高い 。プライオリティエンコーダの真理値表は以下のとおりです。
| 入力 | 出力 | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | で |
| 0 | 0 | 0 | 0 | バツ | バツ | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | バツ | 0 | 1 | 1 |
| 0 | 1 | バツ | バツ | 1 | 0 | 1 |
| 1 | バツ | バツ | バツ | 1 | 1 | 1 |
A1 の論理式を以下に示します。
マーク・ザッカーバーグの教育
論理式
A0 の論理式を以下に示します。
論理式
上記の 2 つのブール関数は次のように実装できます。
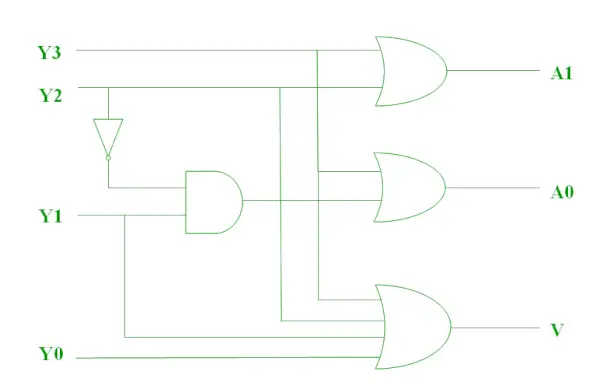
プライオリティエンコーダ
エンコーダで通常発生するいくつかのエラーを以下に示します。
- エンコーダのすべての出力がゼロに等しい場合、あいまいさが生じます。
- 複数の入力がアクティブ High の場合、エンコーダーは出力を生成しますが、その出力は正しいコードではない可能性があります。
したがって、これらの問題を克服するには、エンコーダの各入力に優先順位を割り当てる必要があります。その後、エンコーダの出力は、優先度の高いアクティブ High 入力に対応するコードになります。
エンコーダの応用
- エンコーダは、すべてのデジタル システムで使用される非常に一般的な電子回路です。
- エンコーダは、加算、減算、乗算などのバイナリ関数を実行するために、10 進値を 2 進数に変換するために使用されます。
- 特にプライオリティ エンコーダのその他のアプリケーションには、マイクロプロセッサ アプリケーションでの割り込みの検出が含まれる場合があります。
デジタル ロジックでエンコーダを使用する利点
- 行数の削減: エンコーダは、複数の入力から単一の出力に情報を送信するために必要な回線の数を削減するため、システムの設計を簡素化し、コンポーネントのコストを削減できます。
- 信頼性の向上: エンコーダは、複数の入力を 1 つのシリアル コードに変換することで、情報の送信におけるエラーの可能性を減らすことができます。
- パフォーマンスを向上させた: エンコーダは、複数の入力から単一の出力に情報を送信するのに必要な時間を短縮することで、デジタル システムのパフォーマンスを向上させることができます。
デジタル ロジックでエンコーダーを使用する場合の欠点
- 複雑さの増加: エンコーダは通常、エンコーダに比べてより複雑な回路です。 マルチプレクサ 実装するには追加のコンポーネントが必要です。
- 特定のアプリケーションに限定: エンコーダは、並列入力セットをシリアル コードに変換する必要があるアプリケーションにのみ適しています。
- 柔軟性が限られている: エンコーダは、固定数の入力を固定数の出力にエンコードすることしかできないため、柔軟性が制限されています。
- 結論として、エンコーダは利点と欠点がある便利なデジタル回路です。エンコーダを使用するかどうかの選択は、システムの特定の要件と、複雑さ、信頼性、パフォーマンス、コスト間のトレードオフによって決まります。
GATE CSコーナーの質問
次の質問を練習すると、自分の知識をテストするのに役立ちます。すべての問題は、過去の GATE または GATE 模擬テストで出題されています。実践することを強くお勧めします。
- GATE CS 2013、質問 65
- GATE CS 2014 (セット 3)、質問 65
