デジタルロジックのマルチプレクサ

この記事ではマルチプレクサについて説明します。まずマルチプレクサとは何かを定義し、次にそのタイプである 2×1 と 4×1 について説明し、次に 2×1 マルチプレクサ以上の実装について説明します。低次マルチプレクサを使用したマルチプレクサ。最後に、いくつかのアプリケーション、利点、およびいくつかの FAQ でこの記事を締めくくります。

マルチプレクサとは何ですか?
マルチプレクサの種類
2×1マルチプレクサ
4×1マルチプレクサ
2:1 マルチプレクサによるさまざまなゲートの実装
下位 MUX を使用した上位 MUX の実装
MUX の長所と短所

マルチプレクサとは何ですか?

マルチプレクサとは、組み合わせ回路制御入力または選択入力に応じて、多くのデータ入力と 1 つの出力があります。 N 入力ラインの場合、log2(N) 選択ラインが必要です。2^n入力ラインの場合、n 個の選択ラインが必要です。マルチプレクサは、N 対 1 セレクター、パラレルシリアルコンバーター、多対 1 回路、およびユニバーサルロジック回路としても知られています。これらは主に、一定時間内にネットワーク経由で送信できるデータ量を増やすために使用されます。帯域幅。

マルチプレクサ

マルチプレクサの種類

Mux は入力に基づいてさまざまなタイプになりますが、この記事では、次の 2 つの主要なタイプの Mux について説明します。

2×1マルチプレクサ
4×1マルチプレクサ

2×1マルチプレクサ

2×1 は、1 つを選択するために使用される 2 対 1 マルチプレクサとしても知られる基本的な回路です。信号 2 つの入力から出力を送信します。 2×1 マルチプレクサには 2 つの入力ライン、1 つの出力ライン、および 1 つの選択ラインがあります。マイクロプロセッサなどのデジタルシステムでは、2 つの異なるデータソース間または 2 つの異なる命令間で選択するために使用されるなど、さまざまな用途があります。

真理値表を備えた 2:1 マルチプレクサのブロック図

以下に、2:1 Mux のブロック図と真理値表を示します。このブロック図では、I0 と I1 が入力ライン、Y が出力ライン、S0 が単一の選択ラインです。

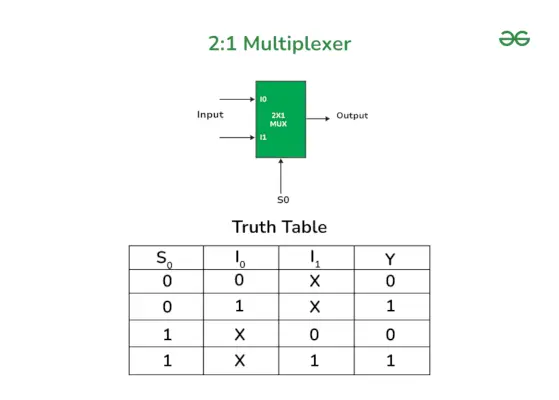
真理値表を備えた 2:1 マルチプレクサのブロック図

2×1 Mux の出力は選択ライン S0 に依存します。

Sが0(ロー)の場合、I0が選択されます。
S0が1(High)の場合、I1が選択されます

2×1 マルチプレクサの論理式

真理値表を使用すると、Mux の論理式は次のように決定できます。

Y=overline{S_0}.I_0+S_0.I_1

2×1マルチプレクサの回路図

真理値表を使用すると、回路図は次のように与えられます

2×1Muxの回路図

4×1マルチプレクサ

4×1 マルチプレクサは、4 対 1 マルチプレクサとも呼ばれます。 4 つの入力と 1 つの出力を持つマルチプレクサです。出力は、選択入力に基づいて 4 つの入力のうちの 1 つとして選択されます。選択行の数は、方程式によって決定される入力の数によって異なります。log_2n,4×1 Mux では、選択ラインは次のように決定できます。log_4=2,slo 2 つの選択が必要です。

4×1マルチプレクサのブロック図

指定されたブロック図では、I0、I1、I2、および I3 は 4 つの入力であり、Y は選択ライン S0 および S1 に基づく単一出力です。

マルチプレクサの出力は、選択ラインのバイナリ値によって決まります。

S1S0=00の場合、入力I0が選択されます。
S1S0=01の場合、入力I1が選択されます。
S1S0=10の場合、入力I2が選択されます。
S1S0=11の場合、入力I3が選択されます。

4×1マルチプレクサの真理値表

以下に示すのは、真理値表 4×1マルチプレクサの

プリティジンタ

4×1マルチプレクサの回路図

真理値表を使用すると、回路図は次のようになります。

マルチプレクサは汎用の組み合わせ回路として機能します。すべての標準論理ゲートはマルチプレクサを使用して実装できます。

2:1 マルチプレクサによるさまざまなゲートの実装

以下に、2:1 Mux を使用した異なるゲートの実装を示します。

2 : 1 Mux を使用した NOT ゲートの実装

2:1 Mux の Not ゲートは次のように取得できます。

入力信号をデータ入力ライン (I0) の 1 つに接続します。
次に、ライン (0 または 1) を他のデータ入力ライン (I1) に接続します。
同じ入力ラインを接続します。D0 に接続されているライン S0 を選択します。

以下は、次の論理表現の図です。 ゲートではありません 2 : 1 マルチプレクサを使用する

2 : 1 Mux を使用した AND ゲートの実装

2:1 Mux の And ゲートは次のように取得できます。

入力 Y を I1 に接続します。
入力 X を選択ライン S0 に接続します。
ライン(0)をI0に接続します。

以下は、次の論理表現の図です。 ANDゲート 2 : 1 マルチプレクサを使用する

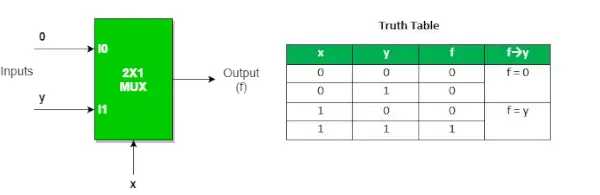
さらに詳しくは、 2 : 1 Mux を使用した AND ゲートの実装

2 : 1 Mux を使用した OR ゲートの実装

2:1 Mux からの OR ゲートは次のように取得できます。

入力 X を選択ライン S0 に接続します。
入力 Y を I1 に接続します。
ライン(1)をI1に接続します。

以下は、次の論理表現の図です。 ORゲート 2 : 1 マルチプレクサを使用する

NAND、NOR、XOR、および XNOR ゲートの実装には 2 つの 2:1 Mux が必要です。最初のマルチプレクサは NOT ゲートとして機能し、補完された入力を 2 番目のマルチプレクサに提供します。

2 : 1 Mux を使用した NAND ゲートの実装

2:1 Mux からの NAND ゲートは次のように取得できます。

最初のマルチプレクサでは、入力、1、0、および y を選択ラインとして受け取ります。
2 番目の MUX では、マルチプレクサからの出力は I1 に接続されます。
line(1)はI0に与えられます。
x は 2 番目の Mux の選択ラインとして指定されます。

以下は、次の論理表現の図です。 NANDゲート 2 : 1 マルチプレクサを使用する

さらに詳しくは、 2 : 1 Mux を使用した NAND ゲートの実装

2 : 1 Mux を使用した NOR ゲートの実装

2:1 Mux の Nor ゲートは次のように取得できます。

最初のマルチプレクサでは、入力、1、0、および y を選択ラインとして受け取ります。
2 番目の MUX では、マルチプレクサからの出力は I0 に接続されます。
line(0) が I1 に与えられます。
x は 2 番目の Mux の選択ラインとして指定されます。

以下は、次の論理表現の図です。 NORゲート 2 : 1 マルチプレクサを使用する

さらに詳しくは、 2 : 1 Mux を使用した NOR ゲートの実装

2 : 1 Mux を使用した EX-OR ゲートの実装

2:1 Mux の Nor ゲートは次のように取得できます。

最初のマルチプレクサでは、入力、1、0、および y を選択ラインとして受け取ります。
2 番目の MUX では、マルチプレクサからの出力は I1 に接続されます。
I0にはyが与えられます。
x は 2 番目の Mux の選択ラインとして指定されます。

以下は、次の論理表現の図です。 EX-ORゲート 2 : 1 マルチプレクサを使用する

2 : 1 Mux を使用した EX-NOR ゲートの実装

以下は、次の論理表現の図です。 EX-ORゲート 2 : 1 マルチプレクサを使用する

Java に相当する

2:1 Mux の Nor ゲートは次のように取得できます。

最初のマルチプレクサでは、入力、1、0、および y を選択ラインとして受け取ります。
2 番目の MUX では、マルチプレクサからの出力は I0 に接続されます。
I1にはyが与えられます。
x は 2 番目の Mux の選択ラインとして指定されます。

下位 MUX を使用した上位 MUX の実装

以下は、低次 MUX を使用した高次 MUX の実装です。

2 : 1 MUX を使用した 4 : 1 MUX

4:1 MUX を実装するには、3 つの 2:1 MUX が必要です。

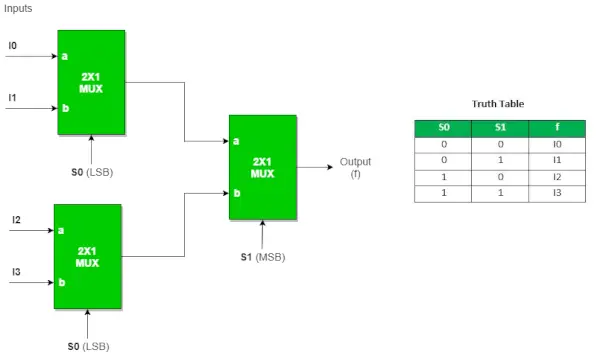
同様に、

8:1 MUX には 7 つの 2:1 MUX が必要ですが、16:1 MUX には 15 の 2:1 MUX が必要で、64:1 MUX には 63 の 2:1 MUX が必要です。したがって、次のような結論を導くことができます。2^n:1MUX に必要なもの(2^n-1) 2:1 MUXes。

4 : 1 MUX を使用した 16 : 1 MUX

以下は、4:1 マルチプレクサを使用した 16:1 マルチプレクサの論理図です。

一般に、 A : 1 MUX を使用して B : 1 MUX を実装するには、1 つの式を使用して同じものを実装します。
B/A = K1、
K1/A = K2、
K2/A = K3

K_N-1/ A = K_N= 1 (MUX の 1 カウントを取得するまで)。

次に、MUX のすべての数を加算します = K1 + K2 + K3 + …。 +K_N。
4:1 MUX を使用して 64:1 MUX を実装するには
上記の式を使用すると、同じ結果を得ることができます。
64 / 4 = 16
16 / 4 = 4
4 / 4 = 1 (MUX の 1 カウントを取得するまで)
したがって、64 : 1 MUX = 16 + 4 + 1 = 21 を実装するには、4 : 1 MUX の合計数が必要です。

f (A、B、C) =sum( 1, 2, 3, 5, 6 ) ドントケア付き (7)

A と B を 4 : 1 MUX の選択ラインとして使用し、

AB を選択: minterm をブール形式に展開すると、C 番目の位置に 0 または 1 の値が表示されるため、そのように配置できます。

ビルダーのデザインパターン

ACを選択 : minterms をブール形式に展開すると、B 番目の位置に 0 または 1 の値が表示されるため、そのように配置できます。

BC を選択として : を展開するミンタームブール形式に変換すると、A の 0 または 1 の値が表示されます。^番目そのように配置できるように配置します。

MUX の長所と短所

MUX の長所と短所は次のとおりです。

MUX の利点

MUX の利点を以下に示します。

効率 : Mux は、制御信号に基づいて複数の入力信号を単一の出力信号にルーティングする効率が優れています。
最適化 : Mux は、ワイヤ、ピン、ケーブルなどのリソースの節約に役立ちます。集積回路（IC）。
異なる実装: Mux を使用して、AND、OR などのさまざまなデジタル論理関数を実装できます。
柔軟性: Mux は要件に従って簡単に構成でき、さまざまなデータソースに対応できるため、システムの汎用性が高まります。

MUX の欠点

MUX の欠点は次のとおりです。

データソースの数が限られている: マルチプレクサが取得できる入力の数は制御線の数によって制限されるため、特定のアプリケーションでは制限が発生する可能性があります。
遅れ： マルチプレクサでは信号パスに遅延が生じる可能性があり、回路のパフォーマンスに影響を与える可能性があります。
複雑な制御理論: マルチプレクサの制御ロジックは、特に多数の入力を備えた大型のマルチプレクサの場合、複雑になる場合があります。
電力使用率: マルチプレクサは、他の単純なマルチプレクサと比較して、より多くの電力を消費する可能性があります。ロジックゲート特に入力数が多い場合に顕著です。

MUXの応用例

MUX のアプリケーションを以下に示します。

データルーティング : Mux は、デジタルシステムのデータルーティングに使用され、複数のデータラインのうち 1 つを選択し、それを出力に再ルーティングします。
データの選択 : Mux は、選択ラインに従ってデータソースを選択するデータ選択に使用されます。
アナログからデジタルへの変換 : Mux は以下で使用されます。 ADC を使用して、別のアナログ入力チャンネルを選択します。
アドレスデコード : Mux は以下で使用されます。マイクロプロセッサまたはアドレスデコード用のメモリ。
ロジック関数の実装 : マルチプレクサを使用して、さまざまな論理関数を実装できます。

結論

この記事では、MUX について説明し、2×1 および 4×1 マルチプレクサであるさまざまなタイプのマルチプレクサについて説明し、2×1 マルチプレクサと低次マルチプレクサを使用した上位マルチプレクサの実装について説明しました。また、その利点、欠点、および用途についても簡単に説明しました。