例 1:
以下に示すように、遷移テーブルの NFA を設計します。
| 現状 | 0 | 1 |
|---|---|---|
| →q0 | q0、q1 | q0、q2 |
| q1 | q3 | e |
| q2 | q2、q3 | q3 |
| →q3 | q3 | q3 |
解決:
遷移図は、表に示すマッピング関数を使用して描画できます。
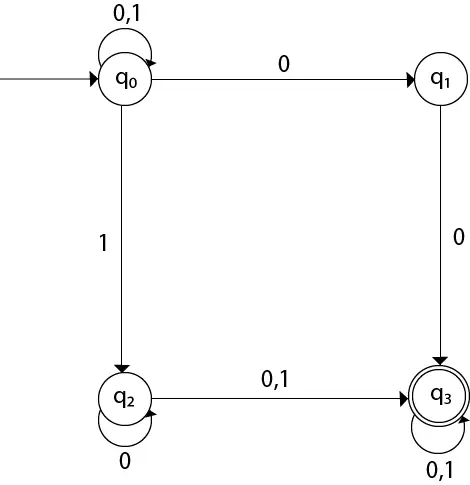
ここ、
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} 例 2:
∑ = {0, 1} で NFA を設計すると、01 で終わるすべての文字列が受け入れられます。
.tostring java
解決:

したがって、NFA は次のようになります。

例 3:
∑ = {0, 1} で 2 つの '1' の後に 2 つの '0' が続く NFA を設計します。
解決:
ダブル 1 の FA は次のとおりです。

直後に 2 つの 0 が続く必要があります。
それから、

double 1 の前には、0 と 1 の任意の文字列を含めることができます。同様に、double 0 の後には、0 と 1 の任意の文字列を含めることができます。
したがって、NFA は次のようになります。

ここで文字列 01100011 を考えます。
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
例 4:
すべての文字列に部分文字列 1110 が含まれる NFA を設計します。
解決:
この言語は、部分文字列 1010 を含むすべての文字列で構成されます。部分的な遷移図は次のようになります。

1010 が部分文字列になる可能性があります。したがって、言語の部分文字列 1010 を維持できるように、入力 0 と 1 を追加します。したがって、NFA は次のようになります。
git すべて追加

上記の遷移図の遷移表は次のようになります。
| 現状 | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1、q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
文字列 111010 を考えてみましょう。
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
捕まってしまった!入力シンボル 0 には q2 からのパスがないため、別の方法で文字列 111010 を処理できます。
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
状態 q5 は受け入れ状態です。全体をスキャンし、最終状態に到達しました。
例 5:
∑ = {0, 1} で NFA を設計すると、右端から 3 番目の記号が常に 0 であるすべての文字列が受け入れられます。
解決:

したがって、右端から 3 番目のシンボルは常に「0」として取得されます。 NFA には次のようなものがあります。

上の画像は NFA です。入力 0 の状態 q0 では、状態 q0 または q1 に進むことができます。
