• 有限状態マシンはパターンを認識するために使用されます。
• 有限オートマトン マシンはシンボルの文字列を入力として受け取り、それに応じて状態を変更します。入力内で、目的のシンボルが見つかると、遷移が発生します。
• 遷移中、オートマトンは次の状態に移行するか、同じ状態に留まることができます。
• FA には、受け入れ状態または拒否状態の 2 つの状態があります。入力文字列が正常に処理され、オートマトンが最終状態に達すると、受け入れられます。

有限オートマトンは次のもので構成されます。

Q: 状態の有限集合
∑: 入力シンボルの有限集合
q0: 初期状態
F: 最終状態
d: 遷移関数

遷移関数は次のように定義できます。

xd xd 意味

 δ: Q x ∑ →Q 

FA は次の 2 つの点で特徴付けられます。

1. DFA (有限オートマトン)
2. NDFA (非決定的有限オートマトン)

DFA

DFA は Deterministic Finite Automata の略です。決定性とは、計算の一意性を指します。 DFA では、入力文字は 1 つの状態のみになります。 DFA は null 移動を受け入れません。これは、DFA が入力文字なしで状態を変更できないことを意味します。

DFA には 5 つのタプル {Q、∑、q0、F、δ} があります。

文字列形式のJava

例

決定論的有限オートマトンの例を参照してください。

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}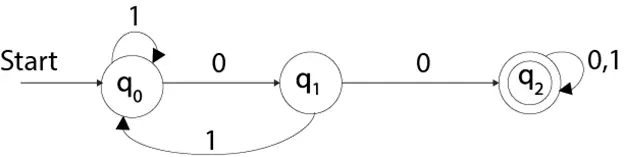 

NDFA

NDFA は、非決定性有限オートマトンを指します。これは、特定の入力の任意の数の状態を遷移するために使用されます。 NDFA は NULL 移動を受け入れます。これは、シンボルを読み取らずに状態を変更できることを意味します。

NDFA にも DFA と同じ 5 つの州があります。ただし、NDFA には異なる遷移関数があります。

bash 文字列の長さ

NDFA の遷移関数は次のように定義できます。

例

非決定性有限オートマトンの例を参照してください。

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}