角度は度 (°) とラジアンで測定されます。多角形の隣接する 2 つの辺の間に形成されます。すべての多角形には異なる辺と異なる数の角度があります。角度を度単位で求める公式は、幾何学や三角法で役立ちます。円弧や円の中心角など、数学の他の概念を理解することが不可欠です。
- 完全な円 = 360°
- 直線 = 180°
- 半円= 180°
- 四半円 = 90°
角度を度単位で計算する
角度を度単位で求めるには、次の 3 つの異なる方法があります。
- プロテクターDの使用
- 直角三角形でのピタゴラスの定理と三角関数の使用
- 角度の和の公式を使用する
- 円の中心角
プロテクターDの使用
プロテクターは、距離をセンチメートルまたはミリメートルで測定するために使用される定規またはスケールの一種です。角度を測定するために使用されるプロテクターは「D」の形をしており、どちらの方向(右または左)からでも 0 ~ 180 ° の角度の値がマークされています。角度を測定するには、軸を D 上の線に合わせる必要があります。プロテクターの中央の円は、測定される角度の頂点に位置合わせされます。角度の頂点に沿った光線は、角度を度単位で見つけるのに役立ちます。
直角三角形でのピタゴラスの定理と三角関数の使用
三角関数には6つの関数がありますが、 サイン、cos、cosec、tan、cot、 そして 秒 直角三角形には、底辺、垂線、斜辺の 3 つの辺があります。
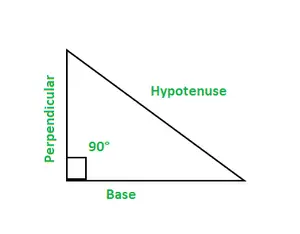
- 底辺: 90°の角度に隣接する辺です。垂直: 90°の角度に隣接する辺です。斜辺: 90°の角度の反対側の辺です。
直角三角形は、角度の一つである90°で表される。三角形の角度の合計は180°です。
- Cosecθ: 斜辺を垂線で割ったものとして表されます。
Cosecθ =
- Cotθ: 底辺を垂線で割ったものとして表されます。
コットθ =
他の三角関数は次のように表されます。
sinθ =
Cosθ =
タンθ =
秒θ =
Cosecθ は 1/sinθ としても表すことができます。
secθは1/cosθとしても表すことができます。
Cotθは1/tanθとしても表すことができます
どこ、
Θは角度です
ピタゴラスの定理
直角の 2 つの辺がわかっていれば、直角三角形の 3 番目の辺を簡単に計算できます。直角三角形では、ピタゴラスの定理は次のように与えられます。
np ゼロ
(斜辺)2= (ベース)2+(垂直)2
角度の和の公式
角度の合計とは、2 つの辺の間に形成される多角形の内角の合計を指します。多角形の辺が 6 つある場合、角は約 6 つあります。他の角度や多角形の角度の合計がわかっていると、角度を見つけるのに役立ちます。
多角形の角度の合計を求める公式は次のようになります。
角度の合計 = 180 (n – 2)
どこ、
n は多角形の辺の数です
例:
- n = 4 の場合、

角度の合計 = 180 (4 – 2)
= 180 (2)
= 360°
n = 5 の場合、
角度の合計 = 180 (5 – 2)
= 180 (3)
= 540°
- n = 6 の場合

角度の合計 = 180 (6 – 2)
= 180 (4)
= 720°
円の中心角
円は、中心点から等距離に境界がある丸い図形です。中心点と境界の間の距離は、円の半径として知られています。円の 2 つの半径によって形成される角度は中心角として知られています。円の中心角の値は 0 ~ 360 度の範囲にあります。

円の中心角を計算する式は次のようになります。
円弧の長さ = 2πr × (θ/360)
Θ = 360L/2pr
どこ、
rは円の半径です
ABは円弧です
シータは度単位の角度です。
L = 円弧の長さ
サンプル問題
問題 1: 半径 2m、円弧長 4m の円の中心角を求めますか?
解決 :
円の中心角を計算する式は次のようになります。
Θ = 360L/2pr
どこ、
rは円の半径です
シータは度単位の角度です。
L = 円弧の長さ
Θ = 角度 (度)
r = 2m
長さ=4m
Θ = 360 × 4 /2 × π × 2
Θ = 114.6°
したがって、円の中心角は 114.6° となります。
問題 2: 半径 10cm、円弧の長さ 18cm の円の中心角を求めますか?
解決 :
円の中心角を計算する式は次のようになります。
Θ = 360L/2pr
どこ、
rは円の半径です
シータは度単位の角度です。
L = 円弧の長さ
r = 10cm
L = 18cm
Θ = 角度 (度)
Θ = 360 × 18 /2 × π × 10
Θ = 103.13°
したがって、円の中心角は 103.13° となります。
質問 3: 他の 3 つの角が 80°、95°、105° である場合、平行四辺形の角度を求めてください。
解決 :
平行四辺形には 4 つの辺があり、角度の合計は 360°です。
角度の合計を求める公式 = 180 (n – 2)
どこ、
n は多角形の辺の数です
ここで、n = 4、
角度の合計 = 180 (4 – 2)
= 180 (2)
= 360°
合計 = 角度 1 + 角度 2 + 角度 3 + 角度 4
360 = 80+95+105+角度4
360 = 280 + 角度 4
角度 4 = 360 – 280
角度 4 = 80°
質問 4: 与えられた図の角度 A を求めます。

解決 :
与えられた値: 斜辺 = 12
垂直 = 6
角度を計算するための三角関数は次のように与えられます。
sinA = 6/12
A = 30°
質問 5: 与えられた図の角度 A を求めます。

解決 :
与えられた値: 斜辺 = 10
ベース= 5
角度を計算する三角関数は次の式で与えられます。
CosA = 5/10
A = 60°
ビープラスツリー
質問 6: 他の 4 つの角が 115°、100°、105°、100° である場合、五角形の角度を求めますか?
解決 :
五角形には5つの辺があり、角度の合計は540°です。
角度の合計を求める公式 = 180 (n – 2)
どこ、
n は多角形の辺の数です
ここで、n = 5、
角度の合計 = 180 (5 – 2)
= 180 (3)
= 540°
合計 = 角度 1 + 角度 2 + 角度 3 + 角度 4 + 角度 5
540 = 115° + 100° + 105°+100° + 角度 5
540 = 420 + 角度 5
Javaでオーバーライドする方法角度 5 = 540 – 420
角度 5 = 120°
質問 7: 与えられた図の角度 A を求めます。

解決 :
与えられた場合: 底 = √3
垂直= 1
角度を計算する三角関数は次の式で与えられます。
タンθ =
Tanθ = 1/√3
A = 30°
質問 8: 他の 3 つの角が 100°、70°、80° の場合、平行四辺形の角度を求めてください。
解決 :
平行四辺形には 4 つの辺があり、角度の合計は 360°です。
角度の合計を求める公式 = 180 (n – 2)
どこ、
n は多角形の辺の数です
ここで、n = 4、
角度の合計 = 180 (4 – 2)
= 180 (2)
= 360°
合計 = 角度 1 + 角度 2 + 角度 3 + 角度 4
360 = 100 + 70 + 80 + 角度 4
360 = 250 + 角度 4
角度 4 = 360 – 250
角度 4 = 110°
したがって、もう一方の角度は 110°です。
質問 9: 他の 5 つの角が 120°、115°、110°、125°、105° である場合、六角形の角度を求めますか?
解決 :
六角形には 6 つの辺があり、角度の合計は 720°です。
角度の合計を求める公式 = 180 (6 – 2)
どこ、
n は多角形の辺の数です
ここで、n = 6、
角度の合計 = 180 (6 – 2)
= 180 (4)
= 720°
合計 = 角度 1 + 角度 2 + 角度 3 + 角度 4 + 角度 5 + 角度 6
720 = 120 + 115 + 110 + 125 + 105 + 角度 6
720 = 575 + 角度 6
角度 6 = 720 – 575
角度 6 = 145°
したがって、六角形の 6 番目の角は 145°です。






