すべての長方形はひし形ですか? 長方形は、4 つの辺と 4 つの角で描かれた 2 次元の幾何学図形です。長方形には、向かい合う辺の長さが等しく、これらの辺が互いに平行になるような辺が含まれます。隣接する辺との角を共有する辺は、その間の角度が 90°です。したがって、長方形には直角が 4 つあります。

目次
矩形
長方形のプロパティは次のとおりです。
- 頂点と呼ばれる 4 つのエッジと 4 つの角があります。
- 長方形の対角線は互いに二等分します。
- 長方形の面積は、その長さと幅の積に相当します。
- 各頂点の角度は 90 度です○
- 長方形の対辺は等しく、互いに平行です。
- 周囲の長さは、長さと幅の合計の 2 倍に相当します。
- すべての内角の合計は 360 度に等しい
長方形の周囲長
長方形の境界を通過することによってカバーされる合計変位を周囲と呼ぶことができます。長さと幅は両方とも単位長さで示されるため、周囲も単位長さで測定されます。
外周は次のように表すことができます。
外周、P = 2 (長さ + 幅)
長方形の面積
平面内で二次元幾何図形が覆う領域を図形の面積といいます。したがって、長方形の面積は、その境界内に含まれる面積です。平方単位で測定されます。面積は長方形の長さと幅の積に相当します。
面積は次のように表すことができます。
面積、A = 長さ × 幅平方単位
長方形の対角公式
幾何学的図形の対角線は交互の頂点を接続します。長方形の対角線の長さは、d で示される次の式で計算できます。
d = sqrt{( l^2 + w^2)} どこ、
l = 長方形の長さ
w = 長方形の幅
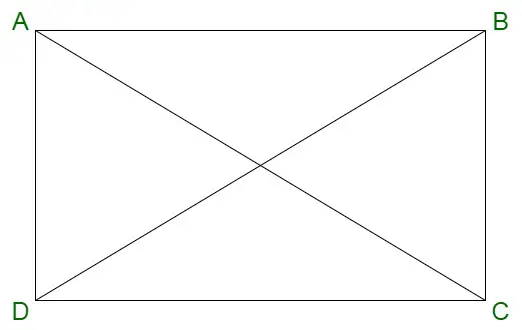
詳細を読む: 長方形のプロパティ: 定義、公式、例
ひし形
ひし形は、4 辺の四角形とも呼ばれます。これは、平行四辺形の特殊なケースであると考えられます。ひし形には、平行な対辺と等しい対角が含まれます。ひし形は、ダイヤモンドまたはひし形ダイヤモンドという名前でも知られています。ひし形には、同じ長さのひし形のすべての辺が含まれます。また、ひし形の対角線は互いに直角に二等分します。
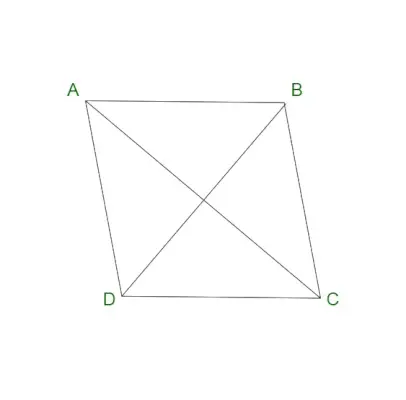
ひし形の性質
ひし形には次のプロパティが含まれます。
- ひし形にはすべての等しい辺が含まれます。
- ひし形の対角線は互いに直角に二等分します。
- 菱形の対辺は本質的に平行です。
- ひし形の隣接する 2 つの角度の合計は 180 に等しい○。
- 菱形の中に内接円はありません。
- 菱形の周囲に外接円はありません。
- ひし形の対角線により、4 つの直角三角形が形成されます。
- これらの三角形は互いに合同です。
- ひし形の対角は等しい。
- ひし形の辺の中点を結ぶと長方形ができます。
- 対角線の半分の中点を結ぶと、別のひし形が形成されます。
ひし形の周囲
ひし形の周囲は、図形を形成する境界線の全長として定義されます。ひし形の 4 つの辺の長さの合計として表すこともできます。ひし形の周囲長は次のように定義されます。
外周、P = 4a 単位
ここで、ひし形の対角線は d で示されます。1&d2「a」は側面です。
ひし形の面積
ひし形の面積は、二次元平面内に囲まれた領域として定義されます。ひし形の面積は、ひし形の対角線の積を 2 で割ったものに相当します。ひし形の面積は、次の式で定義できます。
面積、A =
frac{(d_1 imes d_2)}{2} 平方単位ここで、D1そしてd2ひし形の対角線です。
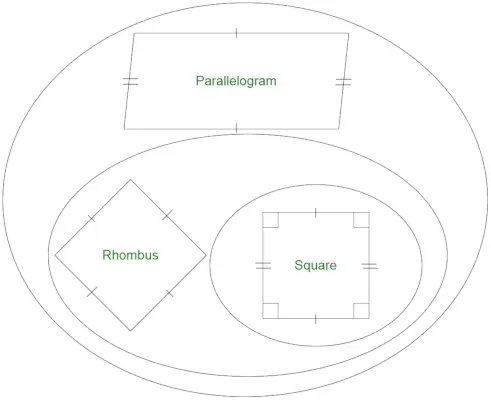
すべてのひし形が平行四辺形であることは簡単にわかりますが、その逆は当てはまりません。正方形は同じ長さの 4 つの辺を含むため、ひし形の特殊なケースと考えることができます。正方形にはすべて直角があります。ただし、ひし形のすべての角が直角であるとは限りません。 。 結論的には、直角を含むひし形は正方形とみなすことができます。したがって、次のように言えます。
- ひし形はすべて平行四辺形です。
- すべての平行四辺形はひし形ではありません。
- すべてのひし形は正方形ではありません。
- すべての正方形はひし形です。
すべての長方形はひし形ですか?
長方形は、すべての等しい辺を含まない幾何学的図形です。正方形は、すべての辺が等しい長方形の特殊なケースです。ご存知のとおり、菱形はすべて等しい辺を持っています。長方形とひし形のセットは、正方形の場合にのみ交差します。したがって、長方形はひし形ではありません。
ハッシュマップ

なぜひし形は長方形なのでしょうか?
ひし形は長方形の特殊なケースです。ひし形の対角線は等しい角度で交差するのに対し、長方形の対角線は長さが等しいことがわかっているためです。ひし形の各辺の中点を結ぶと長方形ができます。
質問例 – すべての長方形はひし形ですか
質問 1. 6 インチの長方形のフレームの面積を計算してください。 長さと幅は3インチです。
解決:
なぜなら、私たちは知っているから、
長方形の面積 = (長さ × 幅) 平方単位。
値を代入すると、次のようになります。
長方形のフレームの面積 = 6 × 3 = 18 平方インチ
問2. 縦12cm、横8cmの長方形の対角線の長さを求めてください。
解決:
私たちは知っています、
対角線の長さ、
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
質問 3. 2 つの対角線の長さが d のひし形の面積を求めます。 1 そしてd 2 それぞれ6cmと12cmになります。
解決:
我々は持っています、
対角線d1= 6cm
対角線d2= 12cm
ひし形の面積は次のように与えられます。
A =
frac{(d_1 imes d_2)}{2} 平方単位A =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36cm2
したがって、ひし形の面積 = 36 cm2。
質問4. ひし形と長方形の違いは何ですか?
解決:
| 財産 | ひし形 | 矩形 |
| 側面 | 等しい辺。 | 対辺は等しい。 |
| 対角線 | 対角線は互いに 90° で二等分します。 対角線は中心で直角になります。 | 対角線は異なる角度で互いに二等分します。一方の角度は鈍角であり、もう一方の角度は鋭角です。 対角線は中心で異なる角度、つまり鈍角と鋭角を作ります。 |
| 角度 | 反対の角は等しい。 隣接する角度を合計すると 180° になります。 | 向かい合う角度と隣り合う角度は等しい。 長方形の隣り合う辺がなす角度は90°です。 |
