積分は数学で広く使用されています。積分セクションでは、分数、単一変数、微分を使用できます。積分は微積分の基本的なオブジェクトです。
積分は主に体積や面積などを求めるために使用されます。
の int 整数記号 ( ∫ )。
モデムとルーターの違い
例えば、
の出力 int x になるだろう ∫×
の mathrm コマンドは導関数を記述するために使用されます。次のように書かれています。
mathrm{d}y どこ d 関数の導出です そして 。要件に応じて変数を変更することもできます。
Javaにいる間に行う
の出力 mathrm{d}x になるだろう ∫dx.
の クアッド コマンドは、テキストと数学変数の間の距離を維持するために使用されます。クワッドに基づく他の間隔コマンドは以下にリストされています。
大きな空間距離を作り出すために使用されます。
中程度の空間距離を作成するために使用されます。
狭い空間距離を作成するために使用されます。
負の空間距離を作成するために使用されます。
例を挙げて理解しましょう。この例は、積分方程式とそれに対応する極限で構成されています。要件に応じて方程式と制限を変更できます。
このような例のコードを以下に示します。
Javaでの挿入ソート
documentclass[12pt]{article} usepackage{mathtools} usepackage{xfrac} egin{document} [ left( int_{0}^{n} f(x),dx
ight)=g(x). ] end{document} 出力
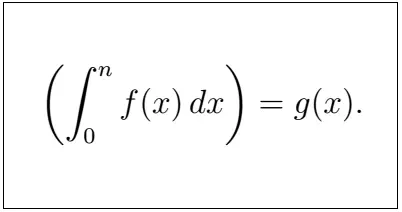
上の方程式に導関数を挿入するには、導関数用のコマンドを追加する必要があります。
このような例のコードを以下に示します。
documentclass[12pt]{article} usepackage{mathtools} usepackage{xfrac} egin{document} [ frac{d}{dy}left( int_{0}^{y} f(x),dx
ight)=g(y). ] end{document} 出力

ご要望に応じてブラケットのタイプを変更することも可能です。
複数の積分
重積分は、さまざまな法則や定理の導出など、数学で使用されます。
例を挙げて重積分をすべて理解しましょう。
ラドヤード・キプリングによる一行ごとの説明の場合
1) 挿入するコード 二重積分 を以下に示します。
documentclass[12pt]{article} usepackage{mathtools} usepackage{xfrac} egin{document} [ iintlimits_B f(x,z),dx,dzqquad integral% the qquad symbol provides the space of 2em between the variables, while quad leaves the space of 1em. ] end{document} 出力

2) 追加するコード 三重項積分 を以下に示します。
documentclass[12pt]{article} usepackage{mathtools} usepackage{xfrac} egin{document} [ iiintlimits_B f(x,y,z) , dx , dy , dz ] end{document} 出力

3) 積分を挿入するコード 四回 すぐに次のように与えられます。
documentclass[12pt]{article} usepackage{mathtools} usepackage{xfrac} egin{document} [ iiiintlimits_B g(w,x,y,z) , dw , dx , dy , dz ] end{document} 出力

製品
積記号は数学でも使用されます。の prod コマンドは、Latex でプロダクト シンボルを指定するために使用されます。
例を挙げて理解しましょう。
カプセル化Java
コードは上記の例と同じになります。違いは次のとおりです。 prod コマンドとその範囲。
このような例のコードを以下に示します。
documentclass[12pt]{article} usepackage{mathtools} usepackage{xfrac} egin{document} [ prod_{i=0}^{N - 1} f(x) ] end{document} 出力

要件に応じて、上記の式と範囲を変更することもできます。
