長さ、幅、高さ 幾何学的図形の寸法で、図形の長さ、幅、高さを示します。長さ、幅、高さは幾何学図形にとって重要なツールです。
この記事では、長さ、幅、高さに関するすべての詳細を学びます。あなたが本物の学生で、長さ、幅、高さについて知りたいなら、ここが正しい場所です。
目次
長さ 幅 高さとは何ですか?
長さ、幅、高さは、オブジェクトの側面または寸法を見つけるために使用されます。図形の最も長い辺が長さ、幅が図形の短い辺、そして図形の垂直方向の寸法が高さと呼ばれます。 2 次元形状 (2D 形状) では長さと幅が使用されますが、3 次元形状 (3D 形状) では長さと幅とともに高さも使用されます。
長さ
2 点間の距離を測定する必要があるツールは、「長さ」として知られています。長さは、図形の最長の寸法を測定するために使用されます。長さは直線の測定値であり、2 点間の距離のみを測定するために使用されます。長さの単位は、メートル、キロメートル、センチメートル、インチなどです。
長さの例として、クリケット場のピッチの長さは 20 メートルであると言えます。
幅
物体や図形の短い距離を測る道具を「幅」といいます。フィギュアの短い方の寸法です。幅は、物体の短い距離のみを測定するために使用される直線的な測定値です。幅の単位は、メートル、キロメートル、センチメートル、インチなどです。
ウェブブラウザの設定
幅の例として、クリケット場のピッチの幅は 5 メートルであると言えます。
身長
高さの別の用語は深さです。高さまたは奥行きは、3D 形状におけるオブジェクトの 3 番目の垂直方向の寸法です。物体の深さや高さを識別します。高さの単位は、メートル、キロメートル、センチメートル、インチなどです。
長さ 幅 高さの寸法の書き方
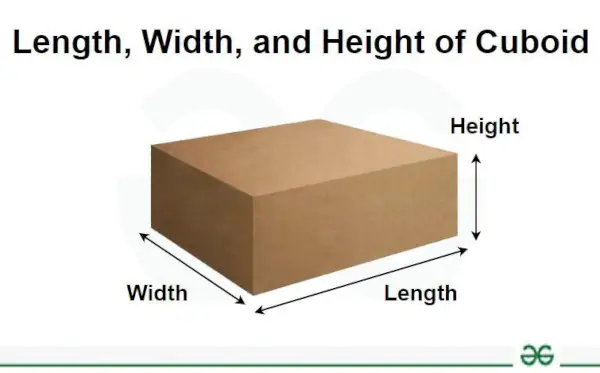
これらのツールの定義をすでに読んだので、長さ、幅、高さの寸法を非常に簡単に書き込むことができます。 2D 幾何学的形状では、長さと幅 (幅) の 2 つの次元のみが得られます。 3D 形状では、長さ、幅、高さの 3 つの寸法がすべて取得されます。図の最も長い辺が長さとしてラベル付けされます。縦方向の寸法は高さまたは奥行きで表記されます。残りの辺は幅または幅と呼ばれます。
この概念は上の図に示されています。これらの寸法の単位は、メートル、センチメートル、インチなどの単位で表されます。
長さ×幅×高さ
3 つの次元をすべて掛け合わせると、幾何学的形状の体積が得られます。体積は、幾何学的形状が占める空間の量として定義されます。の 直方体の体積 は、長さ、幅、高さの乗算に等しい。言い換えれば、3 つの次元をすべて掛け合わせると、直方体または長方形の箱の体積が得られます。
数学的には、直方体の体積 ( 直方体 ) またはボックス = 長さ × 幅 × 高さ。
たとえば、直方体の長さ、幅、高さがそれぞれ 5、8、10 単位の場合、その体積 (V) は次のようになります。
V = 5 × 8 × 10
V = 400 立方体単位
長さと幅
長さと幅はどちらも辺の距離または寸法を測定するために使用されますが、これら 2 つの間には顕著な違いがあります。長さは最も長い寸法であり、幅は最も短い寸法です。長さは常に幅よりも大きくなります。つまり、長さは図形の長辺を示し、幅は図形の短辺を示します。幅(幅)は幾何学的形状の広い性質を示し、長さは形状の長さを示します。
幾何学的形状の 2 つの測定値がそれぞれ 100 cm と 70 cm である場合、100 cm が長さ、70 cm が幅であると簡単に言えます。
長方形の長さ、幅、高さ
長方形は 2D 形状の一例であり、長さと幅のみを持ちますが、長方形の箱または直方体(直方体)は 3D 形状であり、長さ、幅、高さの 3 つの次元をすべて持ちます。したがって、3D の長方形の延長には、長さ、幅、高さが含まれると言えます。
長さ 幅 高さの計算式
長さ、幅、高さは、特定の公式を使用して直方体の体積と表面積を計算するために使用されます。これらの式を以下に示します。
直方体の体積 式
直方体の体積=長さ × 幅 × 身長
直方体の表面積 式
直方体の側面積 = 2 [(長さ × 幅) + (幅 × 身長)]
直方体の総表面積 = 2 [(長さ × 幅) + (幅 × 高さ) + (長さ × 身長)]
長さ 幅 ボックスの高さ
箱の縦、横、高さは形状を見れば簡単に表現できます。一般に、箱の長さは最長辺、幅は短辺、高さは垂直方向の寸法であることがわかっているためです。

一般に、3D 形状の寸法は、長さ、幅または幅、高さが続くように記述されます。これは、箱の寸法を測定する場合は、長さ、幅、高さを記載する必要があることを意味します。たとえば、10 メートル、5 メートル、8 メートルは次のことを示します。
- ボックスの長さ = 10 メートル
- ボックスの幅 = 5 メートル
- ボックスの高さ = 8 メートル
類似記事、
- 2D 形状の領域
- 3D 形状の表面積と体積
長さ 幅 高さ 例
長さ、幅、高さに関する例としては、次のようなものがあります。
例 1: 2D 長方形の庭の寸法は 50 メートルと 35 メートルです。長さと幅の寸法は何ですか?
解決:
みなさんご存じのとおり、
一般的に長い寸法が長さ、短い寸法が幅とみなされます
knn アルゴリズム長さは50メートル、幅は35メートルです。
例2:長方形の箱の寸法がそれぞれ26m、22m、24mの場合。この長方形の箱の高さの値はいくらになるでしょうか?
解決:
Javaの文字列と比較する
ご存知のとおり、3D 形状の寸法は、長さ、幅、高さの順に表現されます。
寸法を考えると、
- 長さ = 26 メートル
- 幅 = 22m
- 高さ = 24 m
つまり、高さは24メートルです
例 3: 直方体の長さ、幅、高さは 6 cm、4 cm、5 cm と与えられます。そのボリュームを決定します。
解決:
考えると、
- 長さ = 6cm
- 幅 = 4cm
- 高さ = 5 cm
体積=長さ×幅×高さ
体積=6×4×5
体積 = 120 cm3
長さ 幅 高さに関する練習問題
長さ、幅、高さに関するいくつかの練習問題は次のとおりです。
問1:長さ12cm、幅8cm、高さ4cmの縦、横、高さを持つ直方体の体積を求めてください。
問2:長さ18m、幅9m、高さ3mの縦、横、高さを持つ直方体の体積を求めてください。
問 3: 長さ、幅、高さ = 42 cm、幅 = 28 cm、高さ = 14 cm の直方体の TSA を求めてください。
問4: 縦、横、高さが長さ7cm、幅5cm、高さ6cmの直方体のLSAを求めてください。
長さ 幅 高さに関するよくある質問
長さ 幅 高さとは何ですか?
長さ、幅、高さは、さまざまな 3D オブジェクトの寸法を測定するために使用されるツールです。
幅と長さではどちらが長いですか?
長さは長い寸法です。長さは通常、物体の長い寸法の測定に使用されます。
オブジェクトがボールのように丸い場合、寸法はどうなりますか?
ボールなどのオブジェクトのさまざまな測定では、オブジェクトが丸い場合、長さ、幅、高さの代わりに半径または直径を使用します。球の「高さ」はその直径に等しい。
体積は常に式の長さによって計算されますか × 幅 × 身長?
3D 形状の場合、体積の公式は一般的に長さ×幅×高さで、その寸法は長さ、幅、高さです。
