以下に等しい は不等式の概念であり、不等式の左側の項が右側の項より大きくてはいけない、つまり、左側の項が右側の項より小さいか、最大でも右側の項と等しくなければならないことを意味します。この記事では、数学における以下の概念について説明し、記号 ≤ とその数直線上での表現を紹介します。数学記号の表、練習問題、不等式に関するよくある質問への回答が含まれています。
目次
ソートされたJavaのリスト
署名に等しい未満
以下の画像では「等号」が追加されています。
以下とは何ですか?
以下とは、あるものが別のものよりも大きくない、または同じである可能性があることを意味します。たとえば、2x – 3 ≤ 9 がある場合、数値 (x) の 2 倍から 3 を引いた値は 9 以下であることを意味します。単純化すると、両辺に 3 を足すと 2x ≤ 12 になります。両辺を 2 で割ると、x ≤ 6 がわかります。つまり、数値 (x) は 6 以下になる可能性があるということですが、これは依然として真実です。
また、チェックしてください
- 小なり記号
- 等号
以下の例
ジョンとピーターが 2 人の友人で、ジョンの年齢がピーター以下であるとします。それは、ヨハネがペテロの年齢より若いか、同じ年齢であることを意味します。言い換えれば、ペテロはヨハネの年齢より年上か、最低でもヨハネと同じ年齢であると言えます。
ここで、ジョンの年齢が x 歳、ピーターの年齢が「y」歳だとすると、Less Than Equal を含む方程式の形でこれを次のように書くことができます。
x ≤ y
どこ、
- x はジョンの年齢です
- y はピーターの年齢です
以下の記号
以下の記号。 ≤です
数学では 2 つの量を比較するために使用されます。具体的には、a ≤ b という場合は、a が b 以下であることを意味します。この記号は、未満 (<) と等しい (=) という概念を組み合わせたものです。したがって、シンボルの左側の値が右側の値より小さいか同じであることを示します。これは、一方が他方より小さいか等しい場合の数値または数式の間の関係を表現するのに役立ちます。
数直線上の以下
数直線上の「以下」という概念は、数値を比較するために使用される基本的な数式です。この文脈では、特定の数値が別の数値以下であることを意味します。この関係を数直線で表すと、小さいか等しい値に対応する点に黒丸(●)が配置されます。たとえば、x ≤ 2 は数直線上で次のように表されます。
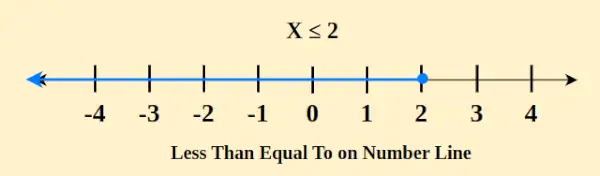
さらに、この点から右に線が伸び、指定された値以上のすべての数値が囲まれます。黒丸を含めることで、エンドポイントが比較の一部であることを強調します。たとえば、A ≤ B の場合、点 A は数直線上の点 B または点 B の左側に位置し、A が B に等しい可能性を包含して、A が B 以下であることを示します。この視覚的表現は、比較された値の相対的な大きさを理解するのに役立ちます。
不等式の記号表記
使用されるさまざまな不等号とその説明を以下に追加します。
| 不等式記号の表記 | |
|---|---|
| 記号の説明 | 記号の表記 |
| 大なり記号 | > |
| 小なり記号 | < |
| 等しい符号 | = |
| 等号に等しくない | ≠ |
| 以上、以下 | ≥ |
| 以下 | ≤ |
等しいより小さいおよび等しいより大きい
以下に「以上」と「以下」の比較を示します。
| 「以上」と「以下」の違い | ||
|---|---|---|
| 側面 | 等しいより大きい | 以下に等しい |
| 意味 | 指定された値以上の値または最小値を示します。 | 指定された値より小さいか最大で等しい値を示します |
| シンボル | ≥ | ≤ |
| 例 | ラムの年齢は10歳以上です ⇒ ラムの年齢 ≥ 10 | ローハンの年齢は15歳未満です ⇒ 露伴の年齢 ≤ 15 |
関連記事 、
- より大きい より小さい
- 以上
- 不平等
以下に等しい – 例
例 1. 不等式を解きます: 3x – 5 ≤ 10。
解決:
まず両辺に 5 を加えます。
3x ≤ 15
次に、3 で割ります: x ≤ 5
Javaの文字列と比較するしたがって、解は x ≤ 5 です
例 2. 不等式を解きます: -2y + 7 ≤ 1。
解決:
両辺から 7 を減算します: -2y ≤ -6
不等号を反転して -2 で割ります: y ≥ 3
解は y ≥ 3 です
以下に等しい – 練習問題
以下の概念に基づいた次の練習問題に挑戦してください。
Q1.不等式を解きます: 2y – 8 は 10 以下です。
Q2. m が 6、n が 3 の場合、m の 2 乗から 5 を引いた値が 2n プラス 1 以下であるかどうかを判断します。
Q3. x を解く: 3x プラス 7 は 22 以下です。
Q4. q が正の数で、4q マイナス 6 が 14 以下である場合、q に取り得る値を見つけます。
Q5.不等式 2a + 5 が 15 以下を満たす a の値の範囲を決定します。
以下に等しい – FAQ
1. 以下とは何ですか?
「以下」は 2 つの値間の関係を示し、最初の値が 2 番目の値より小さいか等しいことを意味します。
2. 以下は数直線上でどのように表されますか?
数直線上では、この関係は、小さいか等しい値に対応する数値の上に黒丸 (●) を配置し、その値以上のすべての数値を含むように右に線を伸ばすことによって視覚的に表されます。
3. 数直線上の黒丸は何を意味しますか?
黒丸は、比較にエンドポイントが含まれていることを強調しています。たとえば、A ≤ B の場合、A が B に等しい可能性を含め、点 A が数直線上の点 B または点 B の左側にあることを示します。
4. 以下の不等式を解く例は何ですか?
不等式 2x – 3 ≤ 9 を考えてみましょう。両辺に 3 を加えると、2x ≤ 12 になります。次に、両辺を 2 で割ると、x ≤ 6 がわかります。したがって、不等式の解は x ≤ 6 となります。
5. 以下または等しいという不平等をどのように解決しますか?
ax + b ≤ c のような不等式を解決するには、通常のアプローチでは、加算、減算、乗算、または除算によって不等式を操作して変数を分離し、不等式を満たす値の範囲を決定します。
6. 以下の記号と以上の記号とは何ですか?
「等しい未満」の記号は次のとおりです ≤ 一方、「以上」の記号は ≧。
