線形回帰とロジスティック回帰

線形回帰とロジスティック回帰は、教師あり学習手法の対象となる 2 つの有名な機械学習アルゴリズムです。どちらのアルゴリズムも本質的に教師ありであるため、これらのアルゴリズムはラベル付きデータセットを使用して予測を行います。しかし、それらの主な違いはその使用方法です。線形回帰は回帰問題の解決に使用され、ロジスティック回帰は分類問題の解決に使用されます。両方のアルゴリズムの説明を相違点の表とともに以下に示します。

線形回帰:

線形回帰は、教師あり学習技術に属する最も単純な機械学習アルゴリズムの 1 つであり、回帰問題を解決するために使用されます。
これは、独立変数を利用して連続従属変数を予測するために使用されます。
線形回帰の目的は、連続従属変数の出力を正確に予測できる最適な直線を見つけることです。
単一の独立変数が予測に使用される場合、それは単純線形回帰と呼ばれ、2 つ以上の独立変数がある場合、そのような回帰は多重線形回帰と呼ばれます。
最適な適合線を見つけることにより、アルゴリズムは従属変数と独立変数の間の関係を確立します。そして、その関係は直線的なものでなければなりません。
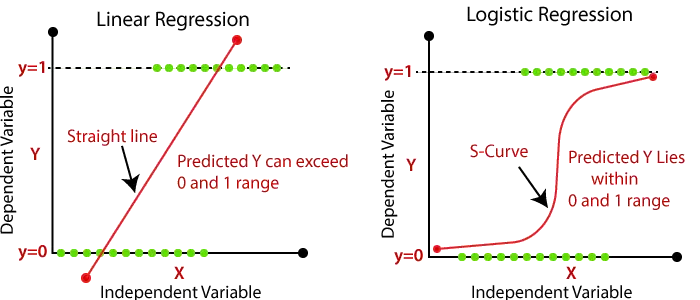
線形回帰の出力は、価格、年齢、給与などの連続値のみである必要があります。従属変数と独立変数の関係は、以下の図に示すことができます。

上の画像では、従属変数は Y 軸 (給与) 上にあり、独立変数は X 軸 (経験) 上にあります。回帰直線は次のように記述できます。

 y= a<sub>0</sub>+a<sub>1</sub>x+ &#x3B5;

どこで、₀そして₁は係数、ε は誤差項です。

ロジスティック回帰:

ロジスティック回帰は、教師あり学習手法に含まれる最も一般的な機械学習アルゴリズムの 1 つです。
これは分類問題にも回帰問題にも使用できますが、主に分類問題に使用されます。
ロジスティック回帰は、独立変数を利用してカテゴリカル従属変数を予測するために使用されます。
ロジスティック回帰問題の出力は 0 と 1 の間のみです。
ロジスティック回帰は、2 つのクラス間の確率が必要な場合に使用できます。今日は雨が降るか降らないか、0か1か、trueかfalseなど。
ロジスティック回帰は、最尤推定の概念に基づいています。この推定によれば、観測されたデータは最も確からしいものとなるはずです。
ロジスティック回帰では、入力の加重合計を、0 から 1 までの値をマッピングできる活性化関数に渡します。このような活性化関数は、として知られています。 シグモイド関数 得られた曲線はシグモイド曲線または S 字曲線と呼ばれます。以下の画像を考えてみましょう。

ロジスティック回帰の方程式は次のとおりです。

線形回帰とロジスティック回帰の違い:

線形回帰	ロジスティック回帰
線形回帰は、指定された一連の独立変数を使用して連続従属変数を予測するために使用されます。	ロジスティック回帰は、指定された一連の独立変数を使用してカテゴリ従属変数を予測するために使用されます。
線形回帰は回帰問題の解決に使用されます。	ロジスティック回帰は、分類問題を解決するために使用されます。
線形回帰では、連続変数の値を予測します。	ロジスティック回帰では、カテゴリ変数の値を予測します。
線形回帰では、出力を簡単に予測できる最適な直線が見つかります。	ロジスティック回帰では、サンプルを分類できる S 曲線を見つけます。
精度の推定には最小二乗推定法を使用します。	精度の推定には最尤推定法を使用します。
線形回帰の出力は、価格、年齢などの連続値である必要があります。	ロジスティック回帰の出力は、0 または 1、Yes または No などのカテゴリ値である必要があります。
線形回帰では、従属変数と独立変数の関係が線形である必要があります。	ロジスティック回帰では、従属変数と独立変数の間に線形関係がある必要はありません。
線形回帰では、独立変数間に共線性がある可能性があります。	ロジスティック回帰では、独立変数間に共線性があってはなりません。