ロジスティック回帰 です 教師あり機械学習アルゴリズム のために使用される 分類タスク ここでの目標は、インスタンスが特定のクラスに属するかどうかの確率を予測することです。ロジスティック回帰は、2 つのデータ要素間の関係を分析する統計アルゴリズムです。この記事では、ロジスティック回帰の基礎、その種類と実装について説明します。
目次
- ロジスティック回帰とは何ですか?
- ロジスティック関数 – シグモイド関数
- ロジスティック回帰の種類
- ロジスティック回帰の仮定
- ロジスティック回帰はどのように機能しますか?
- ロジスティック回帰のコード実装
- ロジスティック回帰のしきい値設定における適合率と再現率のトレードオフ
- ロジスティック回帰モデルを評価するには?
- 線形回帰とロジスティック回帰の違い
ロジスティック回帰とは何ですか?
バイナリにはロジスティック回帰が使用されます 分類 私たちが使う場所 シグモイド関数 、入力を独立変数として受け取り、0 から 1 までの確率値を生成します。
たとえば、クラス 0 とクラス 1 という 2 つのクラスがあり、入力のロジスティック関数の値が 0.5 (しきい値) より大きい場合はクラス 1 に属し、それ以外の場合はクラス 0 に属します。これは回帰と呼ばれます。の延長です 線形回帰 ただし、主に分類問題に使用されます。
キーポイント:
- ロジスティック回帰は、カテゴリ従属変数の出力を予測します。したがって、結果はカテゴリ値または離散値である必要があります。
- これは、Yes または No、0 または 1、true または False などのいずれかになりますが、0 と 1 として正確な値を与えるのではなく、0 と 1 の間にある確率的な値を与えます。
- ロジスティック回帰では、回帰直線を当てはめる代わりに、2 つの最大値 (0 または 1) を予測する S 字型のロジスティック関数を当てはめます。
ロジスティック関数 – シグモイド関数
- シグモイド関数は、予測値を確率にマッピングするために使用される数学関数です。
- 実数値を 0 ~ 1 の範囲内の別の値にマッピングします。ロジスティック回帰の値は 0 ~ 1 の間である必要があり、この制限を超えることはできないため、S 字型のような曲線を形成します。
- S 字曲線はシグモイド関数またはロジスティック関数と呼ばれます。
- ロジスティック回帰では、0 または 1 のいずれかの確率を定義するしきい値の概念が使用されます。しきい値を超える値は 1 になる傾向があり、しきい値を下回る値は 0 になる傾向があります。
ロジスティック回帰の種類
カテゴリに基づいて、ロジスティック回帰は 3 つのタイプに分類できます。
- 二項: 二項ロジスティック回帰では、0 または 1、合格または不合格など、従属変数の可能なタイプは 2 つだけです。
- 多項式: 多項ロジスティック回帰では、猫、犬、羊など、順序付けされていないタイプの従属変数が 3 つ以上存在する可能性があります。
- 序数: 順序ロジスティック回帰では、低、中、高など、3 つ以上の順序付きタイプの従属変数が存在する可能性があります。
ロジスティック回帰の仮定
ロジスティック回帰の仮定を理解することは、モデルを適切に適用していることを確認するために重要であるため、ロジスティック回帰の仮定について検討します。仮定には次のものが含まれます。
- 独立した観測: 各観測は他の観測から独立しています。これは、入力変数間に相関関係がないことを意味します。
- 2 値従属変数: 従属変数は 2 値または二値でなければならない、つまり 2 つの値のみを取ることができるという前提がとられます。 2 つ以上のカテゴリでは、SoftMax 関数が使用されます。
- 独立変数と対数オッズの間の線形関係: 独立変数と従属変数の対数オッズの間の関係は線形である必要があります。
- 外れ値なし: データセットに外れ値があってはなりません。
- サンプルサイズが大きい: サンプルサイズが十分に大きい
ロジスティック回帰に関連する用語
ロジスティック回帰に関連する一般的な用語をいくつか示します。
- 独立変数: 従属変数の予測に適用される入力特性または予測因子。
- 従属変数: 予測しようとしているロジスティック回帰モデルのターゲット変数。
- ロジスティック関数: 独立変数と従属変数が互いにどのように関係するかを表すために使用される式。ロジスティック関数は、入力変数を 0 ~ 1 の確率値に変換します。これは、従属変数が 1 または 0 になる可能性を表します。
- オッズ: 何かが起こっていることと、何かが起こっていないことの比率です。確率とは、発生する可能性のあるすべてに対する何かの発生の比率であるため、確率とは異なります。
- 対数オッズ: ロジット関数としても知られる対数オッズは、オッズの自然対数です。ロジスティック回帰では、従属変数の対数オッズは、独立変数と切片の線形結合としてモデル化されます。
- 係数: ロジスティック回帰モデルの推定パラメータは、独立変数と従属変数が互いにどのように関係しているかを示します。
- インターセプト: ロジスティック回帰モデルの定数項。すべての独立変数がゼロに等しい場合の対数オッズを表します。
- 最尤推定 : ロジスティック回帰モデルの係数を推定するために使用される方法。モデルに基づいてデータを観察する可能性を最大化します。
ロジスティック回帰はどのように機能しますか?
ロジスティック回帰モデルは、 線形回帰 シグモイド関数を使用して連続値出力をカテゴリ値出力に変換する関数です。シグモイド関数は、独立変数入力の実数値セットを 0 から 1 までの値にマッピングします。この関数はロジスティック関数として知られています。
独立した入力特徴を次のようにします。
従属変数は、バイナリ値、つまり 0 または 1 のみを持つ Y です。
次に、入力変数 X に多重線形関数を適用します。
ここ
TCP と IP モデル
上で議論したことはすべて、 線形回帰 。
シグモイド関数
今、私たちは、 シグモイド関数 ここで、入力は z で、0 と 1 の間の確率、つまり予測 y を求めます。
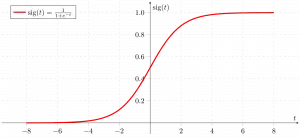
シグモイド関数
上に示したように、Figure シグモイド関数は連続変数データを 確率 つまり、0と1の間です。
sigma(z) 1 に向かう傾向があるz ightarrowinfty sigma(z) として0に向かう傾向がありますz ightarrow-infty sigma(z) 常に 0 と 1 の間に制限されます
ここで、クラスである確率は次のように測定できます。
ロジスティック回帰式
奇数とは、何かが起こることと起こらないことの比率です。確率とは、発生する可能性のあるすべてに対する何かの発生の比率であるため、確率とは異なります。とても奇妙です:
奇数に自然対数を適用します。その場合、対数奇数は次のようになります。
最終的なロジスティック回帰式は次のようになります。
ロジスティック回帰の尤度関数
予測される確率は次のようになります。
- y=1 の場合、予測確率は次のようになります: p(X;b,w) = p(x)
- y = 0 の場合、予測される確率は次のようになります: 1-p(X;b,w) = 1-p(x)
両面から天然丸太を採取
ブール値から文字列へ
対数尤度関数の勾配
最尤推定値を見つけるには、w.r.t w で微分します。
ロジスティック回帰のコード実装
二項ロジスティック回帰:
ターゲット変数は 2 つのタイプのみを持つことができます。0 または 1 は、勝ちか負けか、合格か失敗か、デッドか生きているかなどを表します。この場合、上ですでに説明したように、シグモイド関数が使用されます。
モデルの要件に基づいて必要なライブラリをインポートします。この Python コードは、乳がんデータセットを使用して分類用のロジスティック回帰モデルを実装する方法を示しています。
Python3 # import the necessary libraries from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # load the breast cancer dataset X, y = load_breast_cancer(return_X_y=True) # split the train and test dataset X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23) # LogisticRegression clf = LogisticRegression(random_state=0) clf.fit(X_train, y_train) # Prediction y_pred = clf.predict(X_test) acc = accuracy_score(y_test, y_pred) print('Logistic Regression model accuracy (in %):', acc*100)> 出力 :
ロジスティック回帰モデルの精度 (%): 95.6140350877193
多項ロジスティック回帰:
ターゲット変数には、疾患 A 対疾患 B 対疾患 C のように、順序付けされていない (つまり、タイプに定量的な意味がない) 3 つ以上の可能なタイプを含めることができます。
この場合、シグモイド関数の代わりにソフトマックス関数が使用されます。 ソフトマックス関数 K クラスの場合は次のようになります。
ここ、 K はベクトル z の要素の数を表し、i、j はベクトルのすべての要素を反復します。
この場合、クラス c の確率は次のようになります。
多項ロジスティック回帰では、出力変数には次の値を含めることができます。 2 つ以上のディスクリート出力が可能 。数字データセットについて考えてみましょう。
Python3 from sklearn.model_selection import train_test_split from sklearn import datasets, linear_model, metrics # load the digit dataset digits = datasets.load_digits() # defining feature matrix(X) and response vector(y) X = digits.data y = digits.target # splitting X and y into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1) # create logistic regression object reg = linear_model.LogisticRegression() # train the model using the training sets reg.fit(X_train, y_train) # making predictions on the testing set y_pred = reg.predict(X_test) # comparing actual response values (y_test) # with predicted response values (y_pred) print('Logistic Regression model accuracy(in %):', metrics.accuracy_score(y_test, y_pred)*100)> 出力:
ロジスティック回帰モデルの精度(%): 96.52294853963839
ロジスティック回帰モデルを評価するには?
次の指標を使用してロジスティック回帰モデルを評価できます。
- 正確さ: 正確さ 正しく分類されたインスタンスの割合を示します。
Accuracy = frac{True , Positives + True , Negatives}{Total}
- 精度: 精度 ポジティブな予測の精度に重点を置いています。
Precision = frac{True , Positives }{True, Positives + False , Positives}
- リコール (感度または真陽性率): 想起 すべての実際の陽性インスタンスのうち、正しく予測された陽性インスタンスの割合を測定します。
Recall = frac{ True , Positives}{True, Positives + False , Negatives}
- F1スコア: F1スコア は精度と再現率の調和平均です。
F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}
- 受信機動作特性曲線の下の領域 (AUC-ROC): ROC 曲線は、さまざまなしきい値での真陽性率と偽陽性率をプロットします。 AUC-ROC は、この曲線の下の面積を測定し、さまざまな分類しきい値にわたるモデルのパフォーマンスの総合的な測定値を提供します。
- 適合率-再現率曲線の下の領域 (AUC-PR): AUC-ROCと同様に、 AUC-PR 適合率と再現率の曲線の下の領域を測定し、さまざまな適合率と再現率のトレードオフにわたるモデルのパフォーマンスの概要を提供します。
ロジスティック回帰のしきい値設定における適合率と再現率のトレードオフ
ロジスティック回帰は、決定閾値が考慮された場合にのみ分類手法になります。しきい値の設定はロジスティック回帰の非常に重要な側面であり、分類問題自体に依存します。
しきい値の値の決定は、次の値に大きく影響されます。 精度と再現率。 理想的には、精度と再現率の両方が 1 であることが望ましいですが、これが当てはまることはほとんどありません。
の場合 精度と再現率のトレードオフ 、次の引数を使用してしきい値を決定します。
- 低精度/高再現率: 必ずしも偽陽性の数を減らすことなく偽陰性の数を減らしたいアプリケーションでは、精度の値が低いか再現率の値が高い決定値を選択します。たとえば、がん診断アプリケーションでは、患者が誤ってがんと診断されているかどうかをあまり考慮せずに、影響を受けた患者が影響を受けていないと分類されることは望ましくありません。これは、がんの非存在はさらなる医学的疾患によって検出できるが、すでに拒否された候補では疾患の存在を検出できないためです。
- 高精度/低再現率: 必ずしも偽陰性の数を減らすことなく、偽陽性の数を減らしたいアプリケーションでは、高い値の精度または低い再現率を持つ決定値を選択します。たとえば、パーソナライズされた広告に対して顧客が肯定的に反応するか否定的に反応するかを分類する場合、顧客が広告に対して肯定的に反応することを絶対的に確認したいと考えます。そうしないと、否定的な反応によって潜在的な売上が失われる可能性があります。お客様。
線形回帰とロジスティック回帰の違い
線形回帰とロジスティック回帰の違いは、線形回帰の出力は任意の連続値であるのに対し、ロジスティック回帰はインスタンスが特定のクラスに属するかどうかの確率を予測することです。
線形回帰 | ロジスティック回帰 Javaで配列に追加する |
|---|---|
線形回帰は、指定された一連の独立変数を使用して連続従属変数を予測するために使用されます。 | ロジスティック回帰は、指定された一連の独立変数を使用してカテゴリカル従属変数を予測するために使用されます。 |
線形回帰は回帰問題を解くために使用されます。 | 分類問題を解くために使用されます。 |
ここでは、連続変数の値を予測します。 | ここではカテゴリ変数の値を予測します |
この中で、最適な直線を見つけます。 | この中にS字カーブがあります。 |
精度の推定には最小二乗推定法を使用します。 | 精度の推定には最尤推定法を使用します。 |
出力は、価格、年齢などの連続値である必要があります。 | 出力は、0 または 1、はいまたはいいえなどのカテゴリ値である必要があります。 |
従属変数と独立変数の間に線形関係が必要でした。 | 線形関係は必要ありません。 単純なJavaプログラム |
独立変数間に共線性がある可能性があります。 | 独立変数間に共線性があってはなりません。 |
ロジスティック回帰 – よくある質問 (FAQ)
機械学習におけるロジスティック回帰とは何ですか?
ロジスティック回帰は、バイナリ従属変数、つまりバイナリを使用して機械学習モデルを開発するための統計的手法です。ロジスティック回帰は、データと、1 つの従属変数と 1 つ以上の独立変数の間の関係を説明するために使用される統計手法です。
ロジスティック回帰の 3 つのタイプとは何ですか?
ロジスティック回帰は、二項回帰、多項回帰、順序回帰の 3 つのタイプに分類されます。それらは理論だけでなく実行においても異なります。二項回帰では、「はい」または「いいえ」という 2 つの可能な結果が考慮されます。多項ロジスティック回帰は、値が 3 つ以上ある場合に使用されます。
ロジスティック回帰が分類問題に使用されるのはなぜですか?
ロジスティック回帰は、実装、解釈、トレーニングが簡単です。不明なレコードを非常に迅速に分類します。データセットが線形分離可能である場合、パフォーマンスは良好です。モデル係数は、特徴の重要性の指標として解釈できます。
ロジスティック回帰と線形回帰の違いは何ですか?
線形回帰は連続的な結果を予測するために使用されますが、ロジスティック回帰は観測値が特定のカテゴリに分類される可能性を予測するために使用されます。ロジスティック回帰では、S 字型ロジスティック関数を使用して、0 と 1 の間の予測値をマッピングします。
ロジスティック回帰においてロジスティック関数はどのような役割を果たしますか?
ロジスティック回帰は、ロジスティック関数に依存して出力を確率スコアに変換します。このスコアは、観測値が特定のクラスに属する確率を表します。 S 字型の曲線は、データをしきい値処理してバイナリ結果に分類するのに役立ちます。
