2 つの文字列が与えられると、 S1 そして S2 、タスクは最長共通部分列の長さを見つけること、つまり両方の文字列に存在する最長の部分列を見つけることです。

あ 最長共通部分列 (LCS) は、指定されたすべての入力シーケンスに共通する最長のサブシーケンスとして定義されます。

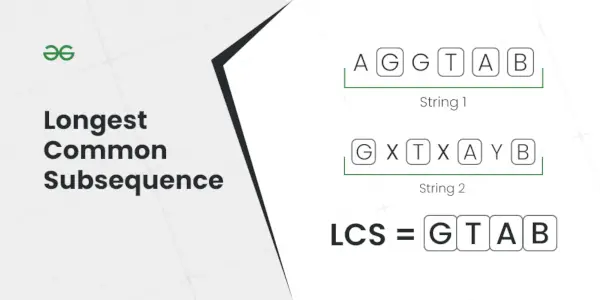
最長共通部分列

例:

入力： S1 = ABC、S2 = ACD
出力： 2
説明： 両方の文字列に存在する最長のサブシーケンスは AC です。

入力： S1 = AGGTAB、S2 = GXTXAYB
出力： 4
説明： 最も長い共通部分列は GTAB です。

入力： S1 = ABC、S2 = CBA
出力： 1
説明： 長さ 1 の共通サブシーケンスは A、B、C の 3 つありますが、長さが 1 を超える共通サブシーケンスはありません。

テキストサイズラテックス

入力： S1 = XYZW、S2 = XYWZ
出力： 3
説明： 長さ 3 の 2 つの共通サブシーケンス XYZ および XYW があり、共通サブシーケンスはありません。長さが3を超えるもの。

Windowsコマンドarp

再帰を使用した最長共通部分列 (LCS):

考えられるすべてのサブシーケンスを生成し、その中で両方の文字列に存在する最長のものを次を使用して見つけます。 このアイデアを実装するには、次の手順に従います。

• 再帰関数を作成します [たとえば lcs() ]。
• 未処理の文字列の先頭文字間の関係を確認します。
  • 関係に応じて、上記のように次の再帰関数を呼び出します。
• 応答として受信した LCS の長さを返します。

以下は再帰的アプローチの実装です。

C++

// A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

C

// A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>b)? a:b; } // ドライバー コード int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int i = 0、j = 0;  // 関数呼び出し printf('LCS の長さは %d', lcs(S1, S2, i, j));  0を返します。 }>>

ジャワ

// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)   n == 0)  return 0;  if (X.charAt(m - 1) == Y.charAt(n - 1))  return 1 + lcs(X, Y, m - 1, n - 1);  else  return max(lcs(X, Y, m, n - 1),  lcs(X, Y, m - 1, n));    // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b)? a:b; } // ドライバー コード public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  文字列 S1 = 'AGGTAB';  文字列 S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('LCS の長さは' + ' ' + lcs.lcs(S1, S2, m, n));  } } // このコードは Saket Kumar によって提供されました>>

パイソン

# A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>

C#

// C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b)? a:b; } // ドライバー コード public static void Main() { String S1 = 'AGGTAB';  文字列 S2 = 'GXTXAYB';  int m = S1.長さ;  int n = S2.長さ;  Console.Write('LCS の長さは' + ' ' + lcs(S1, S2, m, n));  } } // このコードは Sam007 によって提供されました>>

JavaScript

>>

PHP

 // A Naive recursive PHP  // implementation of LCS problem  function lcs($X, $Y, $m, $n)  $n == 0) return 0; else if ($X[$m - 1] == $Y[$n - 1]) return 1 + lcs($X, $Y, $m - 1, $n - 1); else return max(lcs($X, $Y, $m, $n - 1), lcs($X, $Y, $m - 1, $n));  // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; echo 'Length of LCS is '; echo lcs($S1 , $S2, strlen($S1), strlen($S2)); // This code is contributed  // by Shivi_Aggarwal  ?>>>

出力

Length of LCS is 4>

時間計算量: O(2^m+n)
補助スペース: ○(1)

最長共通部分列 (LCS) を使用した メモ化 :

注意して見ると、上記の再帰的解決策には次の 2 つの特性があることがわかります。

1. 最適な下部構造:

L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) の構造を解くには、X[0 の部分構造の助けを借りています。 , 1, …, m-2]、Y[0, 1,…, n-2] を状況に応じて（つまり、それらを最適に使用して）全体の解を見つけます。

2. 重複する副問題:

文字列に対して上記の再帰的アプローチを使用すると、 BD そして あいうえお , 以下に示すような部分再帰ツリーが得られます。ここで、部分問題 L(BD, ABCD) が複数回計算されていることがわかります。ツリー全体を考慮すると、このような重複する部分問題がいくつか存在することになります。

L(AXYT、AYZX)
／＼
L(AXY、AYZX) L(AXYT、AYZ)
/ /
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)

アプローチ： これら 2 つのプロパティが存在するため、動的プログラミングまたはメモ化を使用して問題を解決できます。以下は再帰を使用した解決策のアプローチです。

ダナシュリー・ヴェルマ

• 再帰関数を作成します。また、一意の状態の結果を保存する 2D 配列も作成します。
• 再帰呼び出し中に、同じ状態が複数回呼び出された場合、再計算する代わりに、その状態に対して保存されている答えを直接返すことができます。

上記のアプローチの実装を以下に示します。

C++

// A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { if (m == 0 || n == 0) 0 を返します。  if (X[m - 1] == Y[n - 1]) は dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) を返します。  if (dp[m][n] != -1) { return dp[m][n];  dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); を返します。 } // ドライバー コード int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  ベクター> dp(m + 1, ベクトル (n + 1, -1));  コート<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>

ジャワ

/*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>

パイソン

# A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>

C#

/* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>b)? a:b; } public static void Main() { String s1 = 'AGGTAB';  文字列 s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X.長さ;  int n = Y.長さ;  int[, ] L = 新しい int[m + 1, n + 1];  for (int i = 0; i<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>

JavaScript

/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>

出力

Length of LCS is 4>

時間計算量: O(m * n) ここで、m と n は文字列の長さです。
補助スペース: O(m * n) ここでは、再帰的なスタック領域は無視されます。

ボトムアップ (表形式) を使用した最長共通部分列 (LCS):

次の手順を使用して、LCS の動的プログラミング アプローチを実装できます。

• 2D配列を作成する dp[][] 各入力文字列の長さに 1 を加えたものに等しい行と列を持ちます (行数はインデックスを示します) S1 列はインデックスを示します。 S2 ]。
• dp 配列の最初の行と列を 0 に初期化します。
• dp 配列の行を 1 から繰り返し処理します (たとえば、イテレータを使用します)。 私 ）。
  • それぞれについて 私 からすべての列を反復します。 j = 1 ～ n :
    • もし S1[i-1] に等しい S2[j-1] 、 dp 配列の現在の要素を要素の値に設定します ( dp[i-1][j-1] + 1 ）。
    • それ以外の場合は、dp 配列の現在の要素を次の最大値に設定します。 dp[i-1][j] そして dp[i][j-1] 。
• ネストされたループの後、dp 配列の最後の要素には LCS の長さが含まれます。

より深く理解するには、以下の図を参照してください。

図：

文字列が S1 = アグタブ そして S2 = GXTXAYB 。

最初の一歩： 最初に、最初の行と最初の列が 0 で埋められるサイズ 8 x 7 の 2D 行列 (たとえば、dp[][]) を作成します。

dpテーブルの作成

第二段階： i = 1 についてトラバースします。j が 5 になると、S1[0] と S2[4] は等しくなります。したがって、 dp[][] が更新されます。他の要素については、dp[i-1][j] と dp[i][j-1] の最大値を取ります。 (この場合、両方の値が等しい場合、前の行への矢印を使用しました)。

行番号 1 を埋める

太字のCSS

3 番目のステップ: i = 2 でトラバースすると、S1[1] と S2[0] は同じになります (両方とも「G」)。したがって、そのセルの dp 値が更新されます。残りの要素は条件に従って更新されます。

行番号を入力します。 2

4番目のステップ: i = 3 の場合、S1[2] と S2[0] は再び同じになります。更新内容は以下の通りです。

充填行番号3

5番目のステップ: i = 4 の場合、S1[3] と S2[2] が同じであることがわかります。したがって、dp[4][3] は dp[3][2] + 1 = 2 として更新されます。

列 4 を埋める

6番目のステップ: ここで、i = 5 および j = 5 の場合、S1[4] と S2[4] の値が同じであることがわかります (つまり、両方とも「A」です)。したがって、 dp[5][5] はそれに応じて更新され、3 になります。

行 5 を埋める

最終段階： i = 6 の場合、両方の文字列の最後の文字が同じであることを確認してください (「B」です)。したがって、dp[6][7]の値は4になります。

パワンディープ・ラジャン

最終行を埋める

したがって、共通部分列の最大長は次のようになります。 4 。

以下は、LCS 問題の実装を表にまとめたものです。

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>

ジャワ

// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b)? a:b; public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  文字列 S1 = 'AGGTAB';  文字列 S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('LCS の長さは' + ' ' + lcs.lcs(S1, S2, m, n));  } } // このコードは Saket Kumar によって提供されました>>

パイソン

# Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b)? a:b; } // ドライバー コード public static void Main() { String S1 = 'AGGTAB';  文字列 S2 = 'GXTXAYB';  int m = S1.長さ;  int n = S2.長さ;  Console.Write('LCS の長さは' + ' ' + lcs(S1, S2, m, n));  } } // このコードは Sam007 によって提供されました>>'JavaScript

PHP

 // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>>

出力

Length of LCS is 4>

時間計算量: O(m * n) これは、単純再帰実装の最悪の場合の時間計算量よりもはるかに優れています。
補助スペース: O(m * n) は、アルゴリズムがサイズ (m+1)*(n+1) の配列を使用して共通の部分文字列の長さを格納するためです。

ボトムアップ (空間最適化) を使用した最長共通部分列 (LCS):

• 上記の表作成アプローチでは、L[i-1][j] や L[i][j] などを使用しています。ここで、L[i-1] は行列 L の前の行を指し、L[i] は行列 L を指します。現在の行。
• 以前のベクトルと現在のベクトルの 2 つのベクトルを使用して、空間の最適化を行うことができます。
• 内側の for ループが終了すると、以前と現在の値が初期化されます。

以下に実装を示します。

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector prev(m + 1, 0)、cur(m + 1, 0);  for (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>

ジャワ

// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>

パイソン

def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>

C#

using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>

JavaScript

function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>

出力

Length of LCS is 4>

時間計算量: O(m * n)、これは変わりません。
補助スペース: アルゴリズムではサイズ m の 2 つの配列が使用されるため、O(m) になります。