メモ化とは何ですか?完全なチュートリアル - TECHCODEVIEW.COM

用語 メモ化 ラテン語から来ていますメモ ( 思い出す )、これは一般にアメリカ英語でメモと短縮され、関数の結果を覚えておくべきものに変換することを意味します。

コンピューティングでは、メモ化は、結果の繰り返し計算を排除し、同じ入力を処理する関数の繰り返し呼び出しを回避することにより、コンピュータープログラムを高速化するために使用されます。

メモ化とは何ですか

メモ化とは何ですか?
メモ化が使用される理由>
メモ化をどこで使用するか?
メモ化の種類
動的プログラミングでメモ化テクニックはどのように使用されますか?
- トップダウンアプローチ
- ボトムアップアプローチ
メモ化と表化はどう違うのですか?
メモ化のためのコーディング演習問題
よくある質問
結論

なぜメモ化が使用されるのですか?

メモ化は、次の具体的な形式です。 キャッシング で使用されている 動的プログラミング 。キャッシュの目的は、プログラムのパフォーマンスを向上させ、後で使用できるデータへのアクセスを維持することです。基本的に、部分問題の以前に計算された結果を保存し、保存された結果を同じ部分問題に使用します。これにより、同じ問題について何度も計算するという余分な労力が不要になります。そして、同じ問題が何度も発生する場合、その問題は本質的に再帰的であることはすでにわかっています。

メモ化をどこで使用するか?

メモ化手法を使用できます。 以前に計算された結果の使用 が入ってきます。この種の問題は主に次のような状況で使用されます。再帰、特に次のような問題の場合重複する部分問題。

同じ部分問題が何度も繰り返される例を見てみましょう。

メモ化を使用する場所を示す例:

  Let us try to     find the factorial of a number    .>

以下は、 再帰的メソッド 数値の階乗を求める場合:

int 階乗 (符号なし int n)
{
if (n == 0)
1 を返します。
n * 階乗 (n – 1) を返します。
}

この再帰的手法を使用するとどうなるでしょうか?

上記のスニペットの完全なコードを記述すると、コード内に 2 つのメソッドがあることがわかります。

1. factorial(n) 2. main()>

ここで、2、3、9、5 の階乗を見つけるなど、階乗を見つけるために複数のクエリがある場合は、factorial() メソッドを 4 回呼び出す必要があります。

factorial(2) factorial(3) factorial(9) factorial(5)>

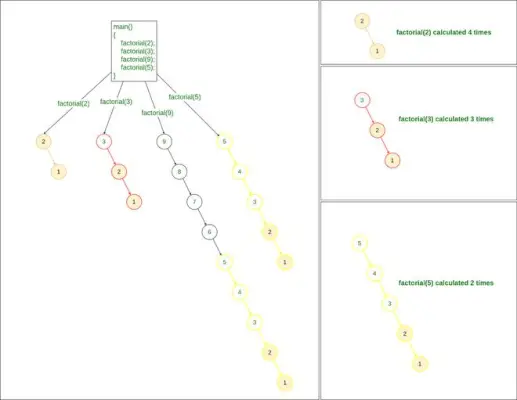
階乗を求める再帰的方法

したがって、K 個の数値の階乗を求めるために必要な時間計算量は次のとおりであると言っても過言ではありません。 O(N*K)

の上） 特定の数値の階乗を求めるには、
矢印) Factorial() メソッドを K 回異なる回数呼び出します。

メモ化はそのような問題にどのように役立つのでしょうか?

上記の問題で、9 の階乗を計算する際に次のようになります。

二分探索のアルゴリズム

2の階乗を計算しています
3 の階乗も計算しています。
5 の階乗も計算しています

したがって、最初の計算時に個々の階乗の結果を保存しておけば、必要な数の階乗をわずか O(1) 時間で簡単に返すことができます。このプロセスは次のように知られています メモ化 。

メモ化を使用した解決策 (メモ化はどのように機能しますか?):

最初に 9 の階乗を見つけて、個々の部分問題の結果を保存すると、O(1) の各入力の階乗を簡単に出力できます。

したがって、メモ化を使用して階乗数を見つけるための時間計算量は次のようになります。 の上）

の上） 最大の入力の階乗を見つけるには
○(1) 各入力の階乗を出力します。

メモ化の種類

メモ化の実装は、問題の解決に関与するパラメーターの変更に依存します。メモ化技術で使用されるキャッシュにはさまざまな次元があります。以下にその一部を示します。

1D メモ化: 関数呼び出しごとに値が定数ではない引数を 1 つだけ持つ再帰関数。
2D メモ化: 関数呼び出しのたびに値が定数ではない引数を 2 つだけ持つ再帰関数。
3Dメモ化 : 関数呼び出しのたびに値が定数ではない引数を 3 つだけ持つ再帰関数。

動的プログラミングではメモ化技術がどのように使用されますか?

動的プログラミングは、重複する部分問題と最適な部分構造特性を持つ問題を効率的に解決するのに役立ちます。動的プログラミングの背後にある考え方は、問題を小さなサブ問題に分割し、将来の使用のために結果を保存することで、結果を繰り返し計算する必要をなくすことです。

動的プログラミングソリューションを定式化するには、次の 2 つのアプローチがあります。

トップダウンのアプローチ: このアプローチは次のとおりです。 メモ化 技術。で構成されています再帰そして キャッシング 。計算において、再帰は関数を繰り返し呼び出すプロセスを表し、キャッシュは中間結果を保存するプロセスを指します。
ボトムアップアプローチ： このアプローチでは、 集計技術動的プログラミングソリューションを実装します。以前と同じ問題に対処しますが、再帰はありません。このアプローチでは、反復が再帰の代わりに使用されます。したがって、スタックオーバーフローエラーや再帰的プロシージャのオーバーヘッドは発生しません。

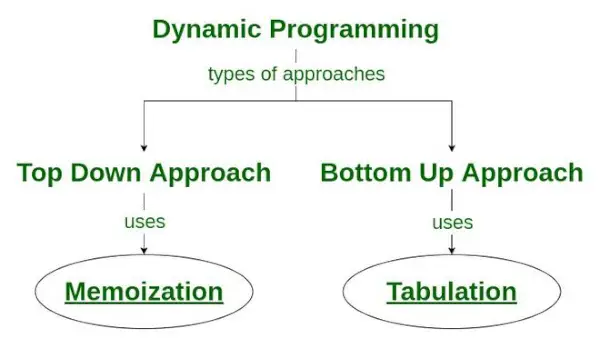
動的プログラミングにおけるメモ化手法の使用方法

メモ化と表化はどう違うのですか?

表化とメモ化

詳細については、以下を参照してください。表化とメモ化

メモ化に関するコーディング演習問題

質問	記事	練習する	ビデオ
n 番目の階段に到達する方法を数えます	ビュー	解決する	時計
単語区切りの問題 \| DP-32	ビュー	解決する	時計
フィボナッチ数のためのプログラム	ビュー	解決する	時計
n番目のカタルーニャ語番号	ビュー	解決する	時計
金鉱山問題	ビュー	解決する	時計
部分集合和問題	ビュー	解決する	時計
ロッドを切る	ビュー	解決する	時計
最小コストパス	ビュー	解決する	時計
終了に到達するまでの最小ジャンプ数	ビュー	解決する	時計
最長の回文部分文字列 \|セット1	ビュー	解決する	時計
最長の繰り返しサブシーケンス	ビュー	解決する	時計
ステップ 1、2、または 3 を使用して n 番目の階段に到達する方法を数えます	ビュー	解決する	時計
N を 1、3、4 の合計として表現するさまざまな方法の数	ビュー	解決する	時計
ある距離をカバーする方法の数を数える	ビュー	解決する	時計
異なる値を持つ連続した要素を持つ配列の数	ビュー	解決する	時計
連続するサブ配列の合計の最大値	ビュー	解決する	時計
最小合計の連続部分配列	ビュー	解決する	時計
障害物のあるグリッド内の固有のパス	ビュー	解決する	時計
m 以上の数値を使用して n を合計するさまざまな方法	ビュー	解決する	時計

メモ化に関するよくある質問 (FAQ)

1: メモ化は DP よりも優れていますか?

メモ化は、動的プログラミングの問題を解決するためのトップダウンのアプローチです。各問題を解いて返された値のメモを作成するため、メモ化と呼ばれます。

2: メモ化はキャッシュと同じですか?

メモ化は実際には特定のタイプのキャッシュです。キャッシュという用語は一般に、将来使用するためのあらゆる保存技術 (HTTP キャッシュなど) を指しますが、メモ化とは、より具体的には値を返すキャッシュ関数を指します。

3: なぜメモ化はトップダウンなのでしょうか?

トップダウンのアプローチでは、大きな問題が複数の下位問題に分割されます。部分問題がすでに解決されている場合は、回答を再利用します。それ以外の場合は、部分問題を解決し、結果をメモリに保存します。

4: メモ化は再帰を使用しますか?

メモ化は、問題を解決するためのトップダウンのアプローチに従います。これは再帰とキャッシュで構成されます。計算において、再帰は関数を繰り返し呼び出すプロセスを表し、キャッシュは中間結果を保存するプロセスを指します。

5: 集計とメモ化のどちらを使用するべきですか?

すべての部分問題を解決する必要がある問題の場合、通常、表作成はメモ化よりも一定の係数で優れています。これは、表作成には再帰のオーバーヘッドがないため、スタックメモリから再帰呼び出しスタックを解決する時間が短縮されます。
元の問題を解決するために部分問題を解決する必要がある場合は常に、部分問題は遅延して解決される、つまり必要な計算のみが実行されるため、メモ化が推奨されます。

6: メモ化はどこで使用されますか?

メモ化は、負荷の高い関数呼び出しの結果をキャッシュし、同じ入力が再び発生したときに結果を返すことによってコンピュータープログラムを高速化するために使用される最適化手法です。

7: なぜメモ化と呼ばれるのですか?

メモ化という用語は、ラテン語の memorandum (記憶する) に由来しており、アメリカ英語では通常、memo と短縮され、関数の結果を記憶すべきものに変換することを意味します。

8: メモ化により時間の複雑さはどのように軽減されますか?

同じ問題を何度も解決するには時間がかかり、プログラム全体の実行時の複雑さが増加します。この問題は、特定の入力に対する問題の既に計算された結果を保存するキャッシュまたはメモリを維持することによって解決できます。そのため、同じ問題を再計算したくない場合は、メモリに保存されている結果を使用するだけで、時間の複雑さを軽減できます。

9: メモ化とキャッシュの違いは何ですか?

メモ化は実際には、入力に基づいて関数の戻り値をキャッシュする特定のタイプのキャッシュです。キャッシュはより一般的な用語です。たとえば、HTTP キャッシュはキャッシュですが、メモ化ではありません。

10: なぜメモ化よりも集計の方が速いのですか?

表作成は反復的であり、部分問題の解決に再帰呼び出しのオーバーヘッドが必要ないため、通常はメモ化よりも高速です。

np.ユニーク

メモ化は、関数呼び出しの結果をキャッシュし、同じ入力が再度発生したときにキャッシュされた結果を返すことによって、再帰的関数や計算量の多い関数の実行を高速化するためにコンピューターサイエンスで使用される手法です。

メモ化の基本的な考え方は、指定された入力セットに対する関数の出力を保存し、同じ入力で関数が再度呼び出された場合にキャッシュされた結果を返すことです。この手法により、特に頻繁に呼び出される関数や時間の複雑さが高い関数の計算時間を節約できます。

メモ化を実装するためのステップバイステップのガイドは次のとおりです。

メモ化を使用して最適化する関数を特定します。この関数では、同じ入力に対してコストのかかる計算が繰り返される必要があります。

関数のキャッシュされた結果を保存するディクショナリオブジェクトを作成します。ディクショナリのキーは関数への入力パラメータである必要があり、値は計算結果である必要があります。

関数の開始時に、入力パラメータがキャッシュディクショナリにすでに存在するかどうかを確認します。存在する場合は、キャッシュされた結果を返します。

入力パラメータがキャッシュディクショナリにない場合は、結果を計算し、入力パラメータをキーとしてキャッシュディクショナリに保存します。

計算結果を返します。

以下は、辞書を使用してメモ化を実装する Python コードの例です。

Python3

def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result>

出力

上記のコードでは、フィボナッチ数列の n 番目の数値を計算する fibonacci という関数を定義します。関数呼び出しの結果を保存するには、キャッシュと呼ばれる辞書オブジェクトを使用します。入力パラメータ n がキャッシュディクショナリにすでに存在する場合は、キャッシュされた結果を返します。それ以外の場合は、フィボナッチ関数の再帰呼び出しを使用して結果を計算し、結果を返す前にキャッシュディクショナリに保存します。

メモ化を使用すると、反復的で高価な計算を行う多くの関数のパフォーマンスを最適化できます。関数呼び出しの結果をキャッシュすることで、不必要な計算を回避し、関数の実行を高速化できます。

結論

メモ化はプログラミングの概念であり、あらゆるプログラミング言語に適用できます。その絶対的な目標は、プログラムを最適化することです。通常、この問題はプログラムが負荷の高い計算を実行するときに発生します。この手法では、以前に計算されたすべての結果がキャッシュされるため、同じ問題について再計算する必要がなくなります。

関連記事：

Python のデコレータを使用したメモ化
JavaScript のメモ化