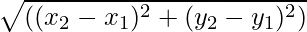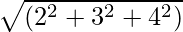logo

TechCodeview

ベクトルの大きさ

ベクトル量は、方向と大きさの両方を持つ量です。ベクトルの大きさはベクトルの長さです。これはベクトルの数値によって与えられ、ベクトルの長さを表すため、常に正になります。あらゆるベクトルに対して 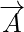overrightarrow{A}その大きさは次のように表されます overrightarrow{A}。

この記事では、ベクトルの大きさの公式、例などについて詳しく学びましょう。

目次



ベクトルの大きさとは何ですか?

ベクトルの大きさは、ベクトルの長さとして定義されます。ベクトルの大きさはベクトルの長さを示すため、常に正になります。任意のベクトル A について、その大きさは |A| として表されます。ベクトルが xi + yj として定義されていると仮定すると、その大きさは個々の項の二乗和の平方根として定義されます。ベクトルの大きさは、ベクトルの長さ、つまりベクトルが持つ価値や影響力を表します。

たとえば、5i N の力が物体に作用する場合、その大きさは 5 N であり、これは加えられる力の強さが 5 N であることを意味します。 私' 5i の は、x の正の方向に適用されることを表します。

ベクトル式の大きさ

ベクトルの大きさを計算するにはさまざまな方法があります。指定されたデータに基づいて、別の種類の公式を使用してベクトルの大きさを求めます。ベクトル A の大きさは、法演算子、つまり |A| を使用して表されます。

ベクトルの大きさをカウントするために使用されるさまざまな公式があります。次の図は、ベクトルの大きさを求めるために使用される重要な式を示しています。

ベクトル式の大きさ

マグニチュードの計算方法は次のとおりです。

  • ベクトル Ā = xi+ yĵ + zk̂ が与えられた場合、ベクトル Ā の大きさは以下の式を使用して計算できます。

ベクトルの大きさ Ā (|A|) = √(x 2 +と 2 +z 2 )

  • 始点ベクトルが (x1、 そして1) であり、ベクトルの終点は (x2、 そして2) が与えられると、ベクトルの大きさが決まります。 overrightarrow{AB}によって与えられます、
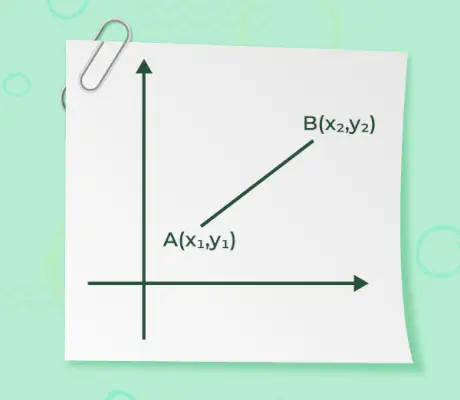
2 つの点が与えられた場合のベクトルの大きさ

ベクトルの始点と終点が指定されている場合、ベクトルの大きさはその点間の距離に他なりません。大きさを求める公式は次のようになります。

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • ベクトルの開始点または終了点のいずれかが原点 o(0, 0) にあり、別の点が A(x, y) 以下の図で指定されているように、
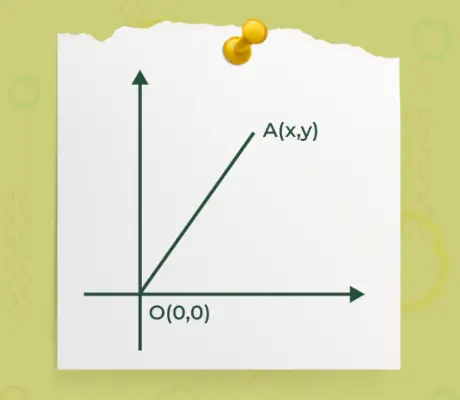
1 つの点と原点が指定された場合のベクトルの大きさ

次に、ベクトルの端の 1 つが原点にある場合のベクトルの大きさを求める式は次のようになります。

|Ā| = √(x 2 +y 2 )

ベクトルの方向

ベクトル量は、大きさと方向の両方を持つ量です。ベクトル量の方向とは、ベクトル量をどの方向に適用するかを示す。これは、ベクトルが水平線または X 軸となす角度として定義されます。という記号で表されます ある 。

下の画像は、ベクトルの方向を示すために使用される矢印を示しています。

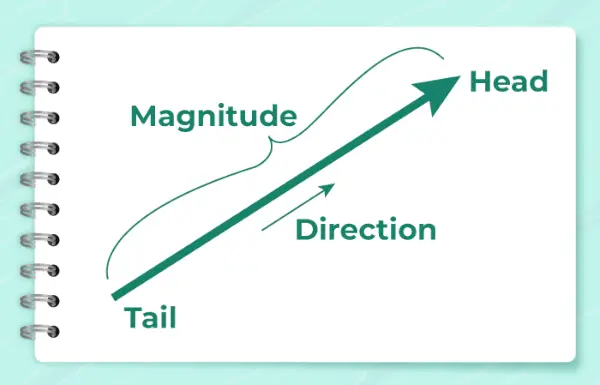
ベクトルの方向

次の式を使用して計算されます。

α = 黄褐色 -1 (y/x)

モデムとルーターの違い

座標 (x) によって生成されたベクトルの場合1、 そして1) と (x2、 そして2) それらの方向は次の式で与えられます。

α = 黄褐色 -1 [（そして 2 - そして 1 ）/（バツ 2 - バツ 1 )]

ベクトルの大きさを見つけるにはどうすればよいですか?

ベクトルの大きさは、以下で説明する手順を使用して計算されます。

ステップ1： ベクトルの x、y、z 成分を特定します。

ステップ2 : すべての x、y、z 成分の 2 乗を求めます。

ステップ 3: ステップ 2 で見つかったすべての正方形を追加します。

ステップ 4: ステップ 3 で取得した合計の平方根を求めます。

ステップ 4 の後に得られる値は、指定されたベクトルの大きさです。

例: ベクトルの大きさを求める A = 3i + 4j

解決：

ベクトル A の大きさは、上で説明した手順を使用して計算されます。

ステップ1： A = 3i + 4j と xi + yj を比較すると、x = 3 と y = 4 が得られます。

ステップ2： バツ2= 32= 9 と y2= 42= 16

ステップ 3: バツ2+と2= 9 + 16 = 25

注意

ステップ 4: √(25) = 5

したがって、ベクトル A = 3i + 4j の大きさは 5 単位です。

結論

結論として、ベクトルの大きさによって、そのベクトルの長さがわかります。この概念は、速度、力、移動方向などの測定に役立つため、物理学、工学、コンピューター サイエンスなどの多くの分野で非常に重要です。ベクトルの大きさを理解することで、実際的な問題をより適切に分析して解決できるようになり、現実世界のアプリケーションで数値や測定値を扱うすべての人にとって重要な知識となります。

続きを読む、

ベクトルの大きさに関する解決例

例 1: ベクトル Ā = 2i + 3ĵ + 4k の大きさを求めます。

解決：

プレオーダートラバーサル

考えると、

Ā = 2i + 3ĵ + 4k

大きさ |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5.38

ベクトルの大きさ 2i+3ĵ+4k は 5.38 ユニット

例 2: ベクトル Ā = 3i + 3ĵ – 6k の大きさを求める

解決：

与えられた

Ā = 3i + 3ĵ – 6k

大きさ |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7.35

ベクトルの大きさ 3i+3ĵ – 6k は 7.35 ユニット。

例 3: ベクトルの始点が (3, 4)、終点が (6, 2) である場合、ベクトルの大きさを求めます。

解決：

考えると、

（バツ1、 そして1) = (3, 4)
（バツ2、 そして2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+(-2)2)
= √(9+4)
= √13 = 3.6

したがって、与えられたベクトルの大きさは次のようになります。 3.6 ユニット。

Javaオブジェクトの等価性

例 4: ベクトルの始点が (2, 1, 4) で終点が (5, 2, 6) である場合、ベクトルの大きさを求めます。

解決：

考えると、

（バツ1、 そして1、 と1) = (2, 1, 4)

（バツ2、 そして2、 と2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3.74

したがって、与えられたベクトルの大きさは次のようになります。 3.74 ユニット。

例 5: 始点と終点 (3, 4) から始まるベクトルの大きさはいくらですか。

解決：

考えると、

ベクトルの始点は O(0, 0) です

終点 (x, y) = (3, 4)

ベクトルの大きさ (|Ā|) = √(x2+y2)

= √(32+42)
= √(9 + 16)
= √25 = 5

したがって、与えられたベクトルの大きさは次のようになります。 5 ユニット。

例 6: 端点の 1 つが原点にあり、もう 1 つの点が (1, 4, 3) にあるベクトルの大きさを求めます。

解決：

考えると、

ベクトルの終点は O(0, 0) です

他の点 (x, y, z) = (1, 4, 3)

ベクトルの大きさ (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5.09

したがって、与えられたベクトルの大きさは次のようになります。 5.09 ユニット。

CSSの下線テキスト

ベクトルの大きさに関する FAQ

ベクトル式の大きさとは何ですか?

ベクトルの大きさはベクトルの数値であり、ベクトルの長さを定義します。任意のベクトル A について、その大きさは |A| として表されます。ベクトルの大きさは次の式を使用して計算されます。

任意のベクトル A = xi + yj + zk について、その大きさは次の式で求められます。

|A| = √(x 2 +と 2 +z 2 )

始点と終点がそれぞれ (x1、 そして1) と (x2、 そして2) その大きさは次の式で与えられます。

|A| = √((x 2 - バツ 1 ) 2 + (そして 2 - そして 1 ) 2 )

ベクトルの大きさを表現するにはどうすればよいでしょうか?

ベクトルの大きさ あ 記号 |A| で表されます。

ベクトルの大きさを見つけるにはどうすればよいですか?

ベクトルの大きさを計算するためにさまざまな式が使用されます。そのうちのいくつかは、

  • |A| = √(x 2 +と 2 +z 2 ) ベクトルが A = xi + yj + zk の形式の場合
  • |A| = √((x) 2 + (そして) 2 ) ベクトルが点 A (x, y) と原点 O(0, 0) によって与えられる場合。
  • |A| = √((x 2 - バツ 1 ) 2 + (そして 2 - そして 1 ) 2 ) ベクトルが点 A (x1、 そして2) と点 B (x2、 そして2）。

マグニチュード 5 のベクトルを見つけます。

大きさが 5 になるさまざまなベクトルがあり、その例としてベクトル A は次のように表されます。

A = 3i + 4j または A = 4i + 5j