慣性モーメントは、回転運動する物体の特性です。慣性モーメントは、回転体の回転運動の変化に対抗する傾向がある回転体の特性です。これは、並進運動におけるあらゆる物体の慣性と同様です。数学的には、慣性モーメントは、各粒子の質量と回転軸からの距離の二乗の積の合計として与えられます。という単位で測定されます。 kgm 2 。
慣性モーメントについては以下の記事で詳しく学びましょう。
目次
慣性モーメントの定義
慣性モーメントは、回転運動における物体の変化に対抗する傾向です。 回転運動 外力によるもの。慣性モーメントは角質量として動作し、回転慣性と呼ばれます。慣性モーメントは機械的慣性モーメントに似ています。 慣性 体の。
MOI は、次の積の合計で表される量として定義されます。 質量 回転運動を実行するすべてのパーティクルの回転軸からの距離の 2 乗で、すべてのパーティクルの距離を計算します。
慣性モーメントの単位
慣性モーメントはスカラー量であり、慣性モーメントの SI 単位は次のとおりです。 kgm 2 。
慣性モーメントの寸法計算式
慣性モーメントは質量と距離の二乗の積として与えられるため。その 次元公式 は質量の寸法式と長さの寸法式の二乗の積で与えられます。慣性モーメントの寸法式は、 ML 2
慣性とは何ですか?
慣性は、その運動状態の変化に抵抗する傾向がある物質の特性です。これは、静止している物体は静止したままで運動を起こそうとする力に抵抗しようとし、運動している物体は運動を続けて運動の大きさを変えようとする力に抵抗しようとすることを意味します。量的には、状態を変えようとする最大の力に等しい。 モーション 。
詳しくはこちら 慣性 。
慣性モーメントの計算式
慣性モーメントは、 スカラー量 。数学的には、粒子の質量の二乗と回転軸からの距離の積は、回転軸の周りの粒子の慣性モーメントと呼ばれます。
オブジェクトの慣性モーメントを求める一般的な公式は次のとおりです。
私=ミスター 2
どこ、
メートル 物体の質量です』
r 回転軸からの距離です
連続した微小な粒子からなる物体の場合、慣性モーメントの計算には慣性モーメントの積分形式が使用されます。
I = ∫dI
私 =
int_{0}^{M} r^2 dm
粒子系の慣性モーメント
粒子系の慣性モーメントは次の式で与えられます。
I = ∑m 私 r 私 2
どこ、
r 私 は i の垂直距離です番目軸からの粒子
メートル 私 は私の質量です番目粒子
上記の慣性モーメントの方程式は、粒子系の慣性モーメントが、各粒子の質量と各粒子の回転軸からの距離の 2 乗の積の和に等しいことを示しています。
以下の図の場合、
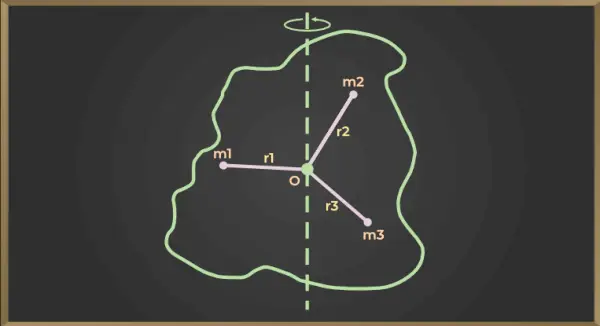
第一粒子の慣性モーメント = m1×r12
第二粒子の慣性モーメント = m2×r22
第三粒子の慣性モーメント = m3×r32
同様に、
慣性モーメント n番目粒子 = mn×rn2
さて、本体全体の回転軸周りの慣性モーメント AB はすべての粒子の慣性モーメントの合計に等しくなりますので、
私 = メートル1×r12+m2×r22+m3×r32+……+mn×rn2
Javaメソッドのオーバーライド
I = Σm 私 ×r 私 2
どこ、
私 回転軸を中心とした本体の慣性モーメントを表します。
メートル 私 は私の質量です番目粒子、
r 私 は i の半径です番目粒子
S 合計を表します。
方程式から、固定軸の周りの物体の慣性モーメントは、その物体の各粒子の質量と固定軸からの垂直距離の二乗の積の合計に等しいと言えます。
慣性モーメントに影響を与える要因
オブジェクトの慣性モーメントは、次の値によって決まります。
- 物体の形と大きさ
- 物体の材質の密度
- 回転軸
慣性モーメントの計算方法
いくつかの方法が使用されます 慣性モーメントを計算する あらゆる回転物体の。
- 均一な物体の場合、慣性モーメントは、その質量と回転軸からの距離 (r) の 2 乗の積を取ることによって計算されます。2)。
- 不均一なオブジェクトの場合、異なる半径ごとの個々の点の質量の積の合計を取ることによって慣性モーメントを計算します。このために使用される式は次のとおりです。
I = ∑m 私 r 私 2
形状別の慣性モーメント計算式
この表では、いくつかの対称オブジェクトの慣性モーメントの式とその回転軸について説明します。

| 物体 | 軸 | 慣性モーメントの表現 |
|---|---|---|
| 中空円筒薄肉 | 中央 | 私=先生2 |
| 細いリング | 直径 | 私 = 1/2 氏2 |
| 環状リングまたは中空円筒 | 中央 | I = 1/2 M(r22+r12) |
| ソリッドシリンダー | 中央 | 私 = 1/2 氏2 |
| ユニフォームディスク | 直径 | I = 1/4 氏2 |
| 中空球体 | 中央 | 私 = 2/3 さん2 |
| ソリッドスフィア | 中央 | I = 2/5 氏2 |
| 均一対称球殻 | 中央 | |
| 均一な板または直方体 | 中央 | I = 1/12 M(a2+b2) |
| 細い棒 | 中央 | I = 1/12 氏2 |
| 細い棒 | ロッドの端で | 私 = 1/3 氏2 |
回転半径
の 回転半径 物体の回転軸から質量点までの垂直距離として定義され、その質量は物体全体の質量に等しく、慣性モーメントは物体の実際の慣性モーメントに等しくなります。物体の総質量がそこに集中していると仮定します。想像上の距離です。回転半径は K で表されます。
物体の質量と回転半径をそれぞれ M と K とすると、物体の慣性モーメントは次のようになります。
私=MK 2 ……(1)
したがって、物体の回転半径は回転軸に垂直であり、その 2 乗にその物体の質量を乗算すると、その軸の周りの物体の慣性モーメントが得られます。
ハッシュテーブルとハッシュマップ
再び式 (1) により、K2=I/M
K = √(I/m)
したがって、軸の周りの物体の回転半径は、その軸の周りの物体の比率の平方根に等しくなります。
慣性モーメントの定理
慣性モーメントに関して非常に重要な 2 種類の定理があります。
- 平行軸定理
- 垂直軸定理
垂直軸定理
垂直軸定理 物体の平面内に位置する 2 つの相互に垂直な軸の周りの物体の慣性モーメントの合計は、2 つの軸に垂直でその点を通過する 3 番目の軸の周りの物体の慣性モーメントに等しいと述べています。交差点の。

上の図では、 牛 そして 株式会社 は、本体の平面内で互いに垂直な 2 つの軸です。 3つ目の軸は、 オズ これは物体の平面に垂直で、物体の交点を通過します。 牛 そして 株式会社 軸。もし 私 バツ 、 私 そして 、 そして 私 と 軸を中心としたボディの慣性モーメントです。 牛 、 株式会社 、 そして オズ それぞれの軸、そしてこの定理によると
私 バツ +私 そして = 私 と
平行軸定理
によると 平行軸定理 、特定の軸の周りの物体の慣性モーメントは、その物体の質量中心を通過する軸の周りの慣性モーメントと、物体の質量の二乗と、物体の質量間の垂直距離の積の合計です。 2つの軸。

上の図で、慣性モーメントを見つける必要があります。 私 ○ 点を通過する体の ○ および平面に垂直な軸の周りで、質量中心を通過する本体の慣性モーメント C そして、与えられた軸に平行な軸の周りには、 私 C 、そして、この定理によると
私 ○ = 私 C +ミリリットル 2
どこ
M 体全体の質量です
私 は 2 つの軸間の垂直距離です。
さまざまな物体の慣性モーメント
さまざまなオブジェクトの慣性モーメントについては、この記事で後述します。
長方形プレートの慣性モーメント
プレートの質量が M、長さ l、幅 b の場合、慣性モーメントは重心を通り、プレートの平面に垂直な軸の周りを通過します。

I = M(l 2 +b 2 /12)
ディスクの慣性モーメント
ディスクの質量が M、半径が r の場合、ディスクの幾何学的軸の周りの慣性モーメントは次のようになります。

I = 1/2(ミスター 2 )
ロッドの慣性モーメント
ロッドの質量が M、長さが l の場合、ロッドの長さに垂直で重心を通る軸の周りの慣性モーメント

I = ミリリットル 2 /12
円の慣性モーメント
リングの質量を M、リングの半径を r とすると、リングの中心に垂直に通る軸の周りの慣性モーメントは次のようになります。

私=先生 2
球の慣性モーメント
固体球の質量が M、半径が r の場合、その直径に関する慣性モーメントは次のようになります。

I = 2/5Mr 2
円柱の慣性モーメント
半径「R」と質量 M の固体円柱の慣性モーメントは次の式で与えられます。

I = 1/2MR 2
中空円筒の慣性モーメント
中空円筒には 2 つの半径、つまり内半径と外半径があります。質量 M、外半径 R を持つ中空円筒の慣性モーメント1、内半径 R2として与えられます

I = 1/2M(R 1 2 +R 2 2 )
中実球の慣性モーメント
質量「M」と半径「R」の固体球の慣性モーメントは次のように与えられます。

I = 2/5MR 2
中空球の慣性モーメント
質量 M、半径「R」の中空球の慣性モーメントは次のように与えられます。

I = 2/3MR 2
リングの慣性モーメント
リングの慣性モーメントは、回転軸が中心を通過する場合と、回転軸が直径を通過する場合の 2 つの場合について与えられます。
中心を通る軸の周りのリングの慣性モーメントは次の式で与えられます。
文字列を int に変換する

私=MR 2
直径を通る軸の周りのリングの慣性モーメントは次の式で与えられます。

私=先生 2 /2
正方形の慣性モーメント
辺「a」の正方形の慣性モーメントは次のように与えられます。

私=a 4 /12
長さ l、質量 M の辺の正方形の板の慣性モーメントは次のように与えられます。
I = 1/6ML 2
三角形の慣性モーメント
三角形の慣性モーメントは、1 つ目は軸が中心を通過する場合、2 つ目は軸が底辺を通過する場合、3 つ目は軸が底辺に垂直な場合の 3 つの状況に対して与えられます。それらの公式を一つずつ見てみましょう。底辺「b」、高さ「h」の三角形の場合、慣性モーメントの公式は次のように与えられます。

軸が図心を通過するとき
私 = bh 3 /36
軸がベースを通過する場合
私 = bh 3 /12
軸がベースに対して垂直の場合
I = (hb/36)(b 2 – b 1 b+b 1 2 )
慣性モーメントと慣性の違い
慣性モーメントと慣性モーメントの違いは次の表に示されます。
| はい・いいえ。 | 慣性 | 慣性モーメント |
|---|---|---|
| 1. | その重要性は直線運動にあります。 | その重要性は回転運動にあります。 |
| 2. | これは、直線運動における物体の状態変化に対抗する物体の特性です。 | 慣性モーメントは、回転運動における物体の状態変化に対抗する物体の特性です。 |
| 3. | 物体の慣性はその質量のみに依存します。 | 物体の慣性モーメントは、その質量と、回転軸に対する質量分布に依存します。 |
| 4. | 物体の慣性は固定されています。 | 物体の慣性モーメントは、回転軸によって異なります。 |
回転体の運動エネルギー
質量「m」の物体が、回転軸からの距離「r」で速度 v で回転すると仮定します。その角速度は ω = v/r で与えられ、v = rω となります。今では、 運動エネルギー 体の値は次によって与えられます
KE = 1/2mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2おお2
⇒ KE = 1/2Iω 2
したがって、回転体の運動エネルギーは、慣性モーメントと慣性モーメントの積の半分で与えられます。 角速度 体の。回転体の運動エネルギーとも呼ばれます。 回転運動エネルギー 。回転運動エネルギーの公式は次のように与えられます。
KE = 1/2Iω 2
慣性モーメント(I)は、本体の角速度には依存しません。これは、回転体の質量と回転軸からの距離の関数です。したがって、角運動は直線運動に類似していることが観察されます。これは、慣性モーメントの重要性が、回転体の回転軸から異なる距離で質量がどのように分布するかについてのアイデアを与えることを意味します。
慣性モーメントの応用
慣性モーメントにはさまざまな用途がありますが、その一部については以下で説明します。
- 慣性モーメントが大きいため、地球はその軸を中心に同じ角速度で回転します。
- 小さな可動ホイールが子供用プレイモーターの下に配置されています。この車輪を地面にこすってモーターから離れると、車輪の慣性モーメントによりモーターはしばらく動き続けます。
- 各エンジンはシャフトに取り付けられた大きくて重い車輪で構成されており、その質量の大部分はその円周上にあります。そのため慣性モーメントが大きいです。この車輪をフライホイールといいます。エンジンのシャフトを駆動するトルクは増加し続けます。したがって、シャフトの回転は均一ではない可能性がありますが、より大きな慣性を持つ移動ホイールの存在により、シャフトはほぼ均一な速度で回転し続けます。
- 牛車、人力車、スクーター、自転車などの車輪では、質量の大部分がその円または縁に集中しています。このフープまたはルーチンは、硬いスポークによってホイールの軸に取り付けられています。こうすることで慣性モーメントが大きくなります。したがって、サイクリング中に脚の動きが止まっても、車輪はしばらく回転し続けます。
また、チェックしてください
- 回転運動の運動学
- 剛体の運動
- ローリングモーション
慣性モーメントに関する解決例
例 1: 質量 500 g の物体が軸の周りを回転しています。回転軸から本体の重心までの距離は 1.2 m です。回転軸を中心とした物体の慣性モーメントを求めます。
解決:
M = 500 g = 0.5 kg とすると、r = 1.2 m となります。
明らかに、物体の質量全体がその質量中心に配置されていると仮定できます。次に、回転軸を中心とした体の慣性モーメントです。
私=先生2
I = 0.5 × (1.2)2
I = 0.72kg・m2
jsp
例 2: 質量 1.2 kg の質量中心から 12 cm 離れた軸の周りの回転半径は 13 cm です。を計算します。 質量の中心を通る軸の周りの回転半径と慣性モーメント。
解決:
とすると、M = 1.0 kg、K = 13 cm、l = 12 cm、KCM= ?、私CM= ?
平行軸の定理より I = ICM+ミリリットル2
K2= KCM2+l2
またはKCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
さて、慣性モーメントⅠCM=MKCM2
私CM= 1.0 × (0.05)2= 2.5 × 10-3kg・m2
例 3: 質量 0.1 kg の物体が軸の周りを回転しています。回転軸から物体の重心までの距離が 0.5 m の場合、物体の慣性モーメントを求めます。
解決:
それを考慮すると、M = 0.1 kg、r = 0.5 m
だから私 = さん2
I = 0.1 × (0.5)2
I = 0.025kg・m2
例 4: 円形リングの平面に垂直な中心を通る軸の周りのリングの慣性モーメントは 200 gm cm です。 2 。直径に関する慣性モーメントはいくらになりますか?
解決:
平面に垂直な別の中心を通過する軸の周りの円形リングの慣性モーメント
氏2= 200グラム・センチメートル2
直径に対する慣性モーメント
= 1/2 MR2
= 1/2 × 200 = 100 gm cm2
慣性モーメントに関する FAQ
慣性モーメントを計算するにはどうすればよいですか?
均一な物体の慣性モーメントを求めるための基本公式は次のとおりです。
私=ミスター 2
どこ、
メートル 物体の質量です』
r 回転軸からの距離です
ビームの慣性モーメントを計算するにはどうすればよいですか?
中心およびそれに水平な軸に沿ったビームの慣性モーメントは、次の式を使用して計算されます。
I = ミリリットル 2 /12
物体の慣性モーメントは何に依存しますか?
物体の慣性モーメントは、以下の要因によって決まります。
- 体の質量、
- 回転軸
- 物体の形と大きさ
慣性モーメントの単位とは何ですか?
慣性モーメントの単位は、 キログラム 2
慣性モーメントが負になることはありますか?
いいえ、慣性モーメントが負になることはありません。
質量慣性モーメントとは何ですか?
慣性質量モーメントは、角運動量または方向の変化に対する物体の抵抗の測定値です。点質量の質量慣性モーメントは、I = mr で与えられます。2粒子系の場合、質量慣性モーメントは I = Σ として与えられます。私メートル私r私2
断面慣性モーメントとは何ですか?
面積慣性モーメントは、平面内の任意の軸に対して点がどのように分散しているかを示す 2D 形状平面のプロパティです。断面慣性モーメントは、断面二次モーメントまたは断面二次モーメントとも呼ばれます。 xy 平面における断面二次モーメントの公式は次のように与えられます。xy= ∫xy dxdxy = ∫xy dA
