分位数-分位数(q-q プロット)プロットは、データセットが特定の確率分布に従っているかどうか、またはデータの 2 つのサンプルが同じものに由来しているかどうかを判断するためのグラフィカルな方法です。 人口 か否か。 Q-Q プロットは、データセットが適切かどうかを評価するのに特に役立ちます。 正規分布 または、他の既知の分布に従っているかどうか。これらは、仮定をチェックし、予想される分布からの逸脱を特定するために、統計、データ分析、品質管理でよく使用されます。
分位数とパーセン位数
分位数は、分布全体の等しい確率または割合を含む間隔にデータを分割するデータセット内の点です。これらは、データセットの広がりや分布を説明するためによく使用されます。最も一般的な分位数は次のとおりです。
- 中央値 (50パーセンタイル) : 中央値は、データセットを最小から最大の順に並べたときの中央の値です。データセットを 2 つの等しい半分に分割します。
- 四分位数 (25、50、75 パーセンタイル) : 四分位数は、データセットを 4 つの等しい部分に分割します。第 1 四分位 (Q1) はデータの 25% が下回る値、第 2 四分位 (Q2) は中央値、第 3 四分位 (Q3) はデータの 75% が下回る値です。
- パーセンタイル : パーセンタイルは四分位に似ていますが、データセットを 100 等分に分割します。たとえば、90 パーセンタイルは、データの 90% が下回る値です。
注記:
- q-q プロットは、2 番目のデータ セットの分位数に対する最初のデータ セットの分位数のプロットです。
- 参考のために、45% の線もプロットされています。 のために サンプルが同じ母集団に由来する場合、点はこの線に沿ったものになります。
正規分布:
正規分布 (別名ガウス分布ベル曲線) は、ランダムに生成された実際の値から得られる分布を表す連続確率分布です。
。 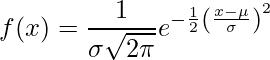

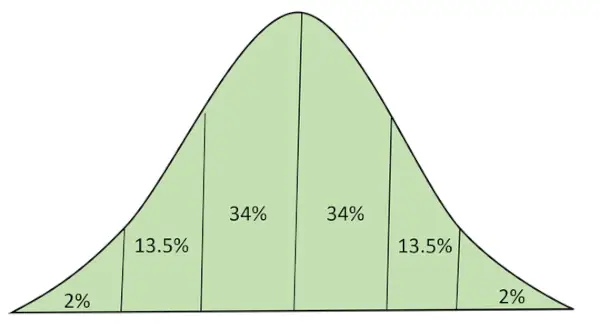
曲線下の面積を持つ正規分布
Q-Q プロットを描くには?
分位数-分位数 (Q-Q) プロットを描画するには、次の手順に従います。
- データを収集する : Q-Q プロットを作成するデータセットを収集します。データが数値であり、対象母集団からの無作為サンプルを表していることを確認してください。
- データを並べ替える :データを昇順または降順に並べます。このステップは、分位数を正確に計算するために不可欠です。
- 理論的な分布を選択する : データセットを比較する理論的な分布を決定します。一般的な選択肢には、正規分布、指数分布、またはデータによく適合するその他の分布が含まれます。
- 理論上の分位数を計算する : 選択した理論的分布の分位数を計算します。たとえば、正規分布と比較する場合は、正規分布の逆累積分布関数 (CDF) を使用して、期待される分位数を見つけます。
- プロット :
- 並べ替えられたデータセット値を X 軸にプロットします。
- 対応する理論的な分位数を y 軸にプロットします。
- 各データ ポイント (x、y) は、観測値と期待値のペアを表します。
- データ ポイントを接続して、データセットと理論上の分布の間の関係を視覚的に検査します。
Q-Q プロットの解釈
- プロット上の点がほぼ直線に沿って配置されている場合は、データセットが想定された分布に従っていることを示唆しています。
- 直線からの逸脱は、想定された分布からの逸脱を示しているため、さらなる調査が必要です。
Q-Q プロットによる分布の類似性の調査
Q-Q プロットを使用して分布の類似性を調査することは、統計学の基本的なタスクです。 2 つのデータセットを比較して、それらが同じ分布に由来するかどうかを判断することは、さまざまな分析目的にとって不可欠です。共通の分布の仮定が成り立つ場合、データセットを結合すると、位置やスケールなどのパラメーター推定の精度が向上します。 Q-Q プロットは、分位数-分位数プロットの略で、分布の類似性を評価するための視覚的な方法を提供します。これらのプロットでは、あるデータセットの分位数が別のデータセットの分位数に対してプロットされます。点が対角線に沿って密接に並んでいる場合、分布間の類似性が示唆されます。この対角線からの逸脱は、分布特性の違いを示します。
のようなテストを行う一方で、 カイ二乗 そして コルモゴロフ・スミルノフ テストでは全体的な分布の違いを評価でき、Q-Q プロットでは分位数を直接比較することで微妙な視点が得られます。これにより、アナリストは、正式な統計テストだけでは明らかではない、場所の変化や規模の変化など、特定の違いを識別できるようになります。
Q-Q プロットの Python 実装
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
出力:
Q-Q プロット
ここで、データ ポイントは Q-Q プロットの直線にほぼ沿っているため、データセットが仮定された理論的分布 (この場合は正規分布であると仮定) と一致していることが示唆されます。
Q-Q プロットの利点
- 柔軟な比較 : Q-Q プロットは、さまざまなサイズのデータセットを比較できます。 等しいサンプルサイズが必要です。
- 無次元解析 : これらは無次元であるため、データセットを比較するのに適しています。 単位やスケールが異なります。
- 視覚的解釈 : 理論上の分布と比較したデータ分布を明確に視覚的に表現します。
- 逸脱に敏感 : 想定された分布からの逸脱を簡単に検出し、データの不一致の特定に役立ちます。
- 診断ツール : 分布の仮定の評価、外れ値の特定、データ パターンの理解に役立ちます。
分位数-分位数プロットの応用
分位数-分位数プロットは次の目的で使用されます。
- 分布の仮定の評価 : Q-Q プロットは、データセットが正規分布などの特定の確率分布に従っているかどうかを視覚的に検査するためによく使用されます。観測データの分位数と仮定された分布の分位数を比較することにより、仮定された分布からの逸脱を検出できます。これは、分布仮定の妥当性が統計的推論の精度に影響を与える多くの統計分析において非常に重要です。
- 外れ値の検出 : 外れ値は、データセットの残りの部分から大きく逸脱したデータ ポイントです。 Q-Q プロットは、予想される分布パターンから大きく外れているデータ ポイントを明らかにすることで、外れ値を特定するのに役立ちます。外れ値は、プロット内の予想される直線から逸脱した点として表示される場合があります。
- ディストリビューションの比較 : Q-Q プロットを使用して 2 つのデータセットを比較し、それらが同じ分布に由来するかどうかを確認できます。これは、あるデータセットの分位数を別のデータセットの分位数に対してプロットすることで実現されます。点がほぼ直線に沿って配置されている場合は、2 つのデータセットが同じ分布から抽出されたことを示唆しています。
- 正常性の評価 : Q-Q プロットは、データセットの正規性を評価するのに特に役立ちます。プロット内のデータ ポイントが直線にほぼ沿っている場合、データセットがほぼ正規分布していることを示します。線からの逸脱は正規性からの逸脱を示唆しており、さらなる調査やノンパラメトリック統計手法が必要になる場合があります。
- モデルの検証 : 計量経済学や機械学習などの分野では、予測モデルを検証するために Q-Q プロットが使用されます。観察された応答の分位数とモデルによって予測された分位数を比較することで、モデルがデータにどの程度適合しているかを評価できます。予想されるパターンからの逸脱は、モデルの改善が必要な領域を示している可能性があります。
- 品質管理 : Q-Q プロットは、経時的または異なるバッチにわたる測定値または観察値の分布を監視するために、品質管理プロセスで使用されます。プロット内の予想されるパターンからの逸脱は、基礎となるプロセスの変化を示す可能性があり、さらなる調査が必要になります。
Q-Q プロットの種類
統計やデータ分析で一般的に使用される Q-Q プロットにはいくつかのタイプがあり、それぞれが異なるシナリオや目的に適しています。
- 正規分布 : データが正規分布に従っている場合、Q-Q プロットはほぼ対角線に沿った点を示す対称分布。
- 右に歪んだ分布 : Q-Q プロットが、観察された分位数が上端に向かって直線から逸脱し、右側の長い裾を示すパターンを表示する分布。
- 左に歪んだ分布 : Q-Q プロットが、観察された分位数が下端に向かって直線から逸脱するパターンを示す分布。これは、左側の長い裾を示します。
- 分散不足の分布 : Q-Q プロットでは、理論上の分位数と比較して対角線の周りに密集した観測分位数が示され、分散が小さいことを示唆する分布。
- 過分散な分布 : Q-Q プロットで観察された分位数がより広がっているか、対角線から逸脱して表示される分布。これは、理論上の分布と比較して、より高い分散または分散を示します。
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
出力:
さまざまな分布の Q-Q プロット
フィズバズ ジャワ
