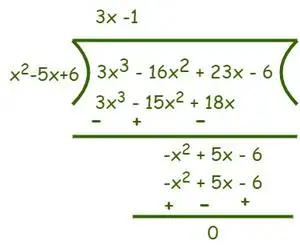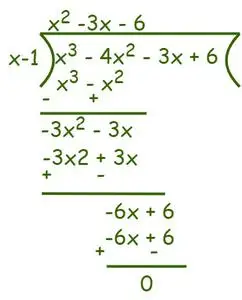3次方程式 は、次数 3 の多項式が定数または最大次数 2 の別の多項式と等価である数学方程式です。三次方程式の標準表現は次のとおりです。 斧 ³ +bx ² +cx+d = 0 ここで、a、b、c、および d は実数です。三次方程式の例としては、次のようなものがあります。 バツ ³ – 4倍 ² + 15x – 9 = 0、 2倍 ³ – 4倍 ² = 0 等

目次

• 多項式の定義
• 方程式の次数
• 3次方程式の定義
• 3次方程式を解くには?
• 3次方程式を解く
• 因数を使用して 3 次方程式を解く
• グラフィカルな手法を使用して 3 次方程式を解く
• 3次方程式の解法に基づく問題
• 3次方程式を解く練習問題

3次方程式の解き方を学ぶには、まず多項式、多項式の次数などについて学ぶ必要があります。この記事では、多項式、多項方程式、3次方程式の解き方、または3次方程式の解き方などについて詳しく学びます。

多項式の定義

多項式は次のように定義されます。

あ 多項式 は、変数の累乗が非負の整数である代数式です。多項式の一般的な形式は次のとおりです。₀バツⁿ+a₁バツ^n-1+a₂バツ^n-2+… +a_n。変数の最大累乗に応じて、多項式は単項式、二項式、三項式などに分類できます。

方程式とは何ですか?

方程式は次のように定義されます。

方程式は、数値またはその他の多項式と同等とみなされる多項式です。たとえば、x + 2 は多項式ですが、x + 2 = 5 は方程式です。同様に、2x + 3 = x + 1 も方程式ですが、2x + 3 と x + 1 は個別に多項式です。

gitステータス

方程式の次数

方程式次数の定義は次のとおりです。

方程式の次数 は、方程式内の変数が持つ最大電力として定義されます。

方程式の次数に基づいて、方程式は次のように分類できます。

• 一次方程式
• 二次方程式
• 3次方程式
• 双二次方程式

一次方程式

変数の最大累乗が 1 となる方程式を線形方程式といいます。

• たとえば、3x +1 = 0

二次多項式

変数の最大累乗が 2 となる方程式は 2 次方程式です。

• たとえば3倍²+x+1 = 0

3次方程式

変数の最大累乗が 3 となる方程式を 3 次方程式といいます。

• たとえば5倍³+3倍²+x+1 = 0

双二次多項式

変数の最大累乗が 4 である方程式を 4 次多項式または 4 次多項式と呼びます。

• たとえば5倍⁴+4倍³+3倍²+2x+1 = 0

3次方程式の定義

3次方程式 は、多項式の最高次数が 3 である代数方程式です。3次方程式の例としては 5x があります。³+3倍²+x+1 = 0、2x³+8 = x ⇒ 2x³-x+8 = 0 など

3 次方程式の一般的な形式は次のとおりです。

斧 ³ +bx ² + cx + d = 0、a ≠ 0

どこ、

• a、b、 そして c は変数の係数とその指数、 d は定数であり、
• a、b、c そして d は実数です。

3次方程式を解くには?

3 次方程式は次数 3 の方程式です。解決策は 3 つあり、以下に追加した手順に従って簡単に解決できます。

ステップ1： 3 次方程式の解をヒット アンド トライ法で 1 つ見つけます。 3 次方程式 P(x) があるとします。次に、x = 0、±1、±2、±3 などを考慮して、任意の x = a、P(a) = 0 を求めます。

ステップ2： P(a) = 0 になったら、P(x) の係数 (x – a) を求めます。

ステップ 3: P(x) を (x – a) で除算すると、多項式除算を使用して二次方程式、たとえば Q(x) が得られます。

ステップ 4: 二次方程式 Q(x) を因数分解して、(x – b) および (x – c) として因数を取得します。

ステップ5: (x – a)、(x – b)、および (x – c) は P(x) の因数であり、各因数を解くと方程式の根 a、b、c が得られます。

詳細については、 除算多項式

3次方程式を解く

あ 3次方程式 2つの方法で解決できます

• それを二次方程式に還元し、因数分解または二次公式のいずれかで解くことによって
• グラフィカルな手法による

あ 3次方程式 根が3つあります。これらのルートは現実のものである場合もあれば、架空のものである場合もあります。また、別個のルート、または 2 つの同じルートと 1 つの異なるルート、および 3 つすべてが同じルートが存在する可能性があります。

あらゆる方程式について注意すべき点 3次方程式 、方程式を解く前に、必ず最初に方程式を標準形式に配置する必要があります。

たとえば、指定された方程式が 2x の場合、²-5 = x + 4/x の場合、これを標準形式、つまり 2x に再配置する必要があります。³-バツ²-5x-4 = 0。これで、適切な方法を使用して方程式を解くことができます。

因数を使用して 3 次方程式を解く

因子定理を使用した 3 次方程式の解法を、以下に追加した例を使用して説明します。

例: 方程式 f(x) = 3x の根を求めます。 ³ −16倍 ² + 23x − 6 = 0。

解決：

与えられた式: f(x) = 3x³−16倍²+ 23x − 6 = 0

まず、多項式を因数分解して根を求めます

定数は -6 なので、考えられる因数は 1、2、3、6 です。

アプレット

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

私たちはそれを知っています、によると 因数定理 f(a) = 0 の場合、(x-a) は f(x) の因数です。

したがって、(x – 2) と (x – 3) は f(x) の因数です。したがって、(x – 2) と (x – 3) の積も f(x) の係数になります。ここで残りの因数を求めるには、長期除算法を使用し、f(x) を (x – 2) と (x – 3) の積で除算します。

したがって、除数 = (x – 2)(x – 3) = (x²– 5x + 6) および配当 = 3x³−16倍²+ 23x − 6. ここで、以下に示すように除算します。

除算後、商として (3x- 1) が得られ、剰余は 0 になります。 除算アルゴリズム 私達はことを知っています 配当 = 除数×商+剰余。

⇒ f(x) = (3x³−16倍²+ 23x − 6) = (x²– 5x + 6)(3x-1)

f(x) = 0 なので

⇒ (ײ– 5x + 6)(3x-1) = 0

⇒ ײ– 5x + 6 = 0 または 3x-1 = 0

x から 2 つの根がすでにわかっているので、3x-1 = 0 ⇒ x = 1/3 を計算します。²– 5x + 6 (2 と 3)

それで、

与えられたもののルーツ 3次方程式 1/3、2、3です。

グラフィカルな手法を使用して 3 次方程式を解く

他の手法を使用して特定の方程式を解くことができない場合、3次方程式はグラフィカルに解きます。したがって、与えられた 3 次方程式を正確に描画する必要があります。方程式が x の項にある場合、方程式の根はグラフが X 軸と交差する点であり、方程式が y の項にある場合、方程式の根はグラフが X 軸と交差する点です。 Y軸をカットします。

3 次方程式の実数解の数は、3 次方程式のグラフが X 軸と交差する回数に等しくなります。

例: 方程式 f(x) = x の根を求めます。 ³ − 4倍 ² − 9x + 36 = 0、グラフィカルな方法を使用。

解決：

与えられた式: f(x) = x³− 4倍²− 9x + 36 = 0。

ここで、与えられた関数のグラフ内の x をランダムな値に置き換えるだけです。

バツ	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

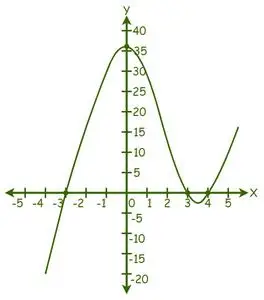
グラフが X 軸を 3 つの点で切断していることがわかります。したがって、実数解は 3 つあります。

グラフから、解は x = -3、x = 3、および x = 4 となります。

したがって、指定された方程式の根は -3、3、4 になります。

続きを読む、

• 一次方程式
• 二次方程式を解く
• 多項式の因数分解

3次方程式の解法に基づく問題

問題 1: f(x) = x の根を求めます ³ – 4倍 ² -3x + 6 = 0。

解決：

フレディ・マーキュリー

与えられた式: f(x) = x³– 4倍²-3x + 6 = 0。

まず、多項式を因数分解して根を求めます。

定数は +6 なので、可能な因数は 1、2、3、6 です。

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

したがって、によると、 因数定理 (x – 1) は、指定された方程式の因数です。ここで、残りの因数を求めるには、長除法を使用します。

によると 除算アルゴリズム 我々は書ける、

したがって、f(x) = x³– 4倍²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 または (x²– 3x – 6) = 0

二次方程式の根は ax であることを知っています。²+ bx + c = 0 は、

x = [-b ± √(b²-4ac)]/2a

したがって、(x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

したがって、指定された 3 次方程式の根は 1、(3+√33)/2、および (3–√33)/2 になります。

問題 2: 方程式 f(x) = 4x の根を求めます ³ – 10倍 ² + 4x = 0。

解決：

与えられた式: f(x) = 4x³– 10倍²+ 4x = 0

⇒ × (4倍²– 10x + 4) = 0

⇒ × (4倍²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 または 4x – 2 = 0、x – 2 = 0

⇒ x = 0 または x = 1/2 または x = 2

したがって、指定された方程式の根は 0、1/2、2 になります。

問題 3: 方程式 f(x) = x の根を求めます ³ +3倍 ² + x + 3 = 0。

解決：

与えられた式: f(x) = x³+3倍²+ x + 3 = 0。

⇒ ײ(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+ 1) = 0

⇒ x + 3 = 0 または x²+1 = 0

⇒ x = -3、±i

したがって、指定された方程式には、実根 (-3) と 2 つの虚根 (±i) があります。

問題 4: 方程式 f(x) = x の根を求めます ³ – 7倍 ² – x + 7 = 0。

解決：

表現を与えられると、

f(x) = x³– 3倍²– 5x + 7 = 0

まず、方程式 f(x) を因数分解します: x³– 3倍²– 5x + 7= 0

これは (x-7)(x+1)(x-1) = 0 と因数分解できます。

多項式を因数分解した後、各因数をゼロに等しくすることで根を求めることができます。例えば：

差分を切り詰めて削除する

• x – 7 = 0、つまり x = 7
• x + 1 = 0、つまり x = -1
• x – 1 = 0、つまり x = 1

したがって、方程式 f(x) の根: x³– 3倍²– 5x + 7 = 0 は

• x = 7
• x = -1
• x = 1

問題 5: 方程式 f(x) = x の根を求めます ³ − 6倍 ² + 11x − 6 = 0、グラフィカルな方法を使用します。

解決：

与えられた式: f(x) = x³− 6倍²+ 11x − 6 = 0。

ここで、与えられた関数のグラフ内の x をランダムな値に置き換えるだけです。

バツ	1	2	3	4	5
f(x)	0	0	0	6	24

グラフが X 軸を 3 つの点で切断していることがわかります。したがって、実数解は 3 つあります。

グラフから、解は x = 1、x = 2、および x = 3 となります。

したがって、指定された方程式の根は 1、2、および 3 になります。

3次方程式を解く練習問題

以下に3次方程式に関する各種練習問題を追加しました。これらの問題を解いて、「3次方程式の解き方」の概念を完全に理解してください。

P1. 3次方程式を3回解く³+2倍²– 11x + 7 = 0。

P2。 3次方程式の根を求めます、4x³– 12倍²+ 17 = 0。

P3. 3 次方程式 x を解きます。³+4倍²– x + 3 = 0 (グラフィカルな方法を使用)。

P4. -9xを満たす数値を見つけてください³+11倍²– 8x + 2 = 0。

3次方程式の解き方に関するFAQ

1. 3次方程式とは何ですか?

3 次方程式は、変数の最大累乗が 3 である代数方程式です。

2. 3 次方程式をどのように因数分解しますか?

3 次方程式は 2 つの方法で因数分解できます。まず、与えられた三次方程式から共通の一次式を取得すると、積として一次式と二次式が得られます。この二次方程式をさらに因数分解して、すべての因数を取得することができます。 2 番目の方法は、ランダムな値を入力して、指定された 3 次方程式のゼロを見つけることです。方程式の値がゼロになる値は、指定された 3 次方程式のゼロの 1 つになります。次に、因数定理を使用して一次式を作成し、たとえば x-a とします。指定された 3 次方程式をこの式で割ると、商として 2 次方程式が得られます。この得られた二次方程式をさらに因数分解してすべての因数を求めることができます。

3. 三次方程式をグラフィカルに解くにはどうすればよいですか?

3次方程式を解くには、指定された3次方程式にxのランダムな値をグラフィカルに入力して解くと、yの値が得られます。得られた値をグラフにプロットします。グラフが x 軸と交差する座標を見つけます。これらの座標は 3 次方程式の解です。

4. すべての 3 次方程式を正確に解くことができますか?

奇数の累乗を持つ方程式には 1 つの実根がなければなりません。したがって、判別式が 0 未満の場合に両方の根が虚数になる可能性がある 2 次方程式とは異なり、3 次方程式には少なくとも 1 つの実根が必要です。

5. 3 次方程式には複数の解が存在しますか?

はい、3 次方程式は最大 3 つの異なる実根を持つことができるため、3 次方程式には複数の解が存在します。

6. 方程式の次数とは何を意味しますか?

方程式内の変数が持つ最大累乗は、多項式の次数と呼ばれます。

7. 多項式と方程式の違いは何ですか?

多項式は、変数の累乗が非負の整数である単純な代数方程式です。この多項式が数値または別の多項式と等価 (=) される場合、それは方程式と呼ばれます。

差分を切り詰めて削除する

8. 3次方程式の因子定理とは何ですか?

因子定理では、r が 3 次方程式 ax の根 (解) である場合、³+bx²+ cx + d = 0 の場合、x – r は方程式の因数です。

9. 数式を使用しても正確な解決策が見つからない場合はどうすればよいですか?

正確な解を見つけることが不可能と思われる場合は、反復法 (ニュートン法など) のような数値的手法を使用して方程式の根を近似することができます。

詳しくはこちら ニュートン・ラフソン法 。