3 の平方根は正の実数であり、それ自体を掛けると 3 になります。 3 の平方根は、終端も反復もない小数であるため、無理数です。 3 の平方根は √3 または 3 と表されます。1/2。 3 の 2 乗は無理数であるため、正確な 10 進数値が計算されることはありません。
3 の平方根の値、√3 =1.732 (切り捨て)
この記事では、3の平方根について詳しく学びます。
目次
3の平方根とは何ですか?
数値の平方根は、それ自体を乗算すると元の数値になる数値です。
例: 4×4 = 16 なので、16 の平方根は 4 なので、√16 = 4
3 の平方根、または単にルート 3 と呼ばれる無理数は、それ自体を乗算すると数値 3 になります。ルート 3 の近似値は次のように与えることができます。
- 10 進形式: 1.732
- 指数形式: 31/2
- 部首形: √3
数学におけるルート 3 の値
数学では、任意の数値の平方根を求めることは非常に重要です。完全二乗の平方根は簡単に計算できます。不完全な正方形の場合、平方根を見つけるのは難しく、通常は長除法を使用して計算されます。
3 の根は √3 で表されますが、これは無理数であるため、10 進数値を計算することはできません。部首形では (3) のように表されます。1/2。 3 の平方根を小数点第 7 位まで四捨五入すると、1.7320508 になります。
3 の平方根 = 1.7320508075688772…
3 の平方根は有理ですか、それとも無理ですか?
平方根 3 は非終端および非反復小数であり、すべての非終端および非反復小数は無理数に該当します。したがって、√3 は 無理数 。
3 の平方根を 10 進展開すると、
√3 = 1.7320508075688772…
繰り返しも終端もないので、√3 は無理数であると確かに言えます。
Javaの同等のインターフェース
3の平方根を求めるにはどうすればよいですか?
完全な平方の平方根を計算するのは常に簡単ですが、非完全な平方の平方根を計算するには、長除法を実行する必要があります。
3 の平方根を計算するには、以下の手順に従う必要があります。
ステップ1: 割り算を容易にするために、3 を 3.000000 と書きます (ゼロは常にペアの形で保持されます)。
ステップ2: 次に、3 未満の完全な正方形、つまり 1 を探し、その数値をそれで割ります。
ステップ 3: ここで、商は 1 で、余りは 2 です。商に小数を入れ、さらに除算するために 0 のペアを取り除きます。
ステップ 4: 次の被除数は 200 で、次の除数は 2X になります (商 1 が前の除数 1 に加算され、X は 10 位になります)。数値 2X と X の乗算は 200 未満になります。これにより、次のようになります。次の値 27 を新しい除数として使用します。
ステップ5: ここで、小数点以下の商に 7 が追加されるため、商の値は 1.7 になり、新しい約数は 27 に 7 を加算することによって取得され、つまり 34Y になります (Y は 100 の位)。前の手順を使用して続行し、商の 3 の平方根を取得します。
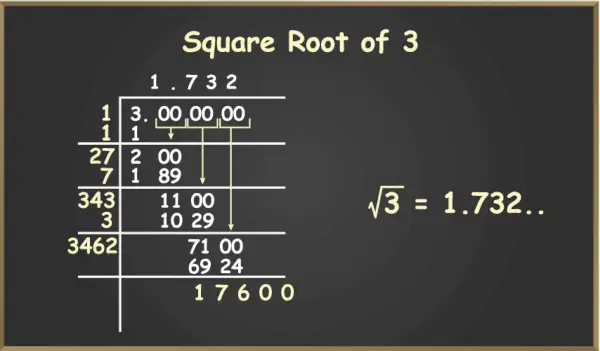
3 の平方根
次に、次のゼロのペアを降ろし、ステップ 4 と 5 を繰り返します。 2 の平方根の正確な値は小数点以下の桁数が無限になるため、これは無限ステップに対して実行できます。約 1 秒間使用できるため、結果を小数点以下 4 桁まで計算できます。平方根の値。
数値の平方根の性質
数値の平方根のさまざまな特性については以下で説明します。
- 完全平方数には完全平方根があります。
- 偶数完全平方の平方根は偶数です。
- 奇数の完全平方根の平方根は奇数です。
- 負の数の平方根は、 複素数 。
平方根の表
さまざまな数値の平方根は数学で広く使用されています。以下の表は、一般的に使用されるさまざまな数値の平方根を示しています。
| 番号 | 平方根 |
|---|---|
| 1 | √(1) = 1 |
| 2 | √(2) = 1.414 (およそ) |
| 3 | √(3) = 1.732 (およそ) |
| 4 | √(4) = 2 |
| 5 | √(5) = 2.236(およそ) |
| 9 | √(9) = 3 |
| 16 | √(16) = 4 |
| 25 | √(25) = 5 |
また、チェックしてください
- 2 の平方根
- 実数
- 有理数
3 の平方根に関する FAQ
3の平方根の値は何ですか?
3 の平方根の近似値は 1.73205 です。
3 の平方根が無理数なのはなぜですか?
3 の平方根の値は、繰り返しも終端もない小数であるため、無理数です。
数字の3は完全正方形ですか?
3 は素数であり、素数には 1 とそれ自身以外の因数はありません。したがって、3 は完全な正方形ではないと言えます。
√3 の値はどうやって求めればよいでしょうか?
√3 の値は、長除法を使用して求めることができます。 3 は完全な正方形ではないため、その正確な値は決して見つかりません。
ルート 2 の値は何ですか?
ルート 2 は無理数であるため、その正確な 10 進数値は決して見つかりません。ルート 2 の近似値は、 √2 = 1.414 (およそ)
