プリズムの表面積の計算式、プリズムの例と種類

プリズムの表面積: 数学では、角柱は多面体ファミリーの重要なメンバーであり、横方向の長方形または平行四辺形の面で接続された、互いに向かい合う 2 つの同一の多角形を持つ 3 次元形状として定義されます。同一の多角形は、三角形、正方形、長方形、五角形、またはその他の n 角形の多角形であり、角柱の底面と呼ばれます。プリズムの他の面は、平行四辺形または長方形です。

この記事では、 さまざまな種類のプリズムとプリズムの表面積を例と演習問題とともに説明します。

プリズムの表面積とは何ですか?
さまざまな種類のプリズム

三角柱
直方体
角柱
五角柱
六角柱

プリズムの表面積の計算式
プリズムの表面積の解決例
プリズムの表面積に関する練習問題

プリズムの表面積とは何ですか?

プリズムの表面積は、そのすべての面で囲まれた総面積と呼ばれます。プリズムの表面積を決定するには、プリズムの各面の面積を計算し、結果の面積を加算する必要があります。プリズムには、側面積と全表面積の 2 種類の表面積があります。 2 つの平行な面 (プリズムの底面) を除いた、プリズムの面が占める面積を側面面積といいます。

プリズムの側表面積 = [底周×高さ] 平方単位

さて、プリズムの総表面積は、その 2 つの底面の面積と側面の表面積の合計です。

あらゆるタイプの直角プリズムの総表面積を計算するための一般式は次のとおりです。

プリズムの総表面積 = [2 (ベース面積) + (ベース周囲 × 高さ)] 平方単位

さまざまな種類のプリズム

プリズムには、プリズムの底面の形状に基づいてさまざまな種類があります。

三角柱、
四角柱、
直方体プリズム、
五角柱、
六角柱、
八角柱。

三角柱

底面が三角形のプリズムを三角プリズムといいます。三角柱は、3 つの傾斜した長方形の面と 2 つの平行な三角形の底面で構成されます。三角柱の高さを H とします。 a、b、c は辺の長さ、h は三角形の底辺の高さです。

CPLD対FPGA

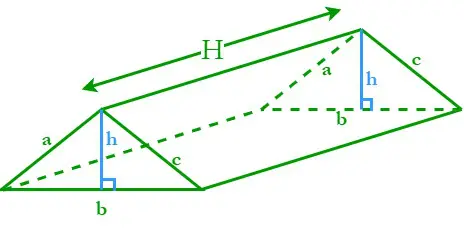
三角形の底辺の周囲長 (P) = 3 辺の合計 = a + b + c

三角形の底辺の面積 (A) = 1/2 × 底辺 × 高さ = 1/2 bh

の一般式は次のとおりであることがわかっています。 直角柱の側面の面積は L.S.A. = PH です。ここで、P は底面の周囲長、A は底面の面積です。

一般式のすべての値を代入すると、次のようになります。 、

三角柱の側表面積 = (a + b +c)H 平方単位

どこ、

a、b、c は三角形の底辺の辺です

Hは三角柱の高さ

直角柱の総表面積の一般式は次のとおりであることがわかっています。 T.S.A. = PH+2A、ここで、P は底部周囲長、A は底部面積、H はプリズムの高さです。

一般式のすべての値を代入すると、次のようになります。

三角柱の総表面積 = (a + b + c)H + 2 × (1/2 bh)

三角柱の総表面積 = (a + b + c)H + bh 平方単位

どこ、

a、b、c は三角形の底辺の辺です

Hは三角柱の高さ

hは三角形の高さです

直方体

底面が長方形のプリズムを直角プリズムといいます。直角プリズムは、4 つの長方形の面と 2 つの平行な長方形の底面で構成されます。 プリズムの高さを h、長方形の底辺の長さと幅をそれぞれ l と w とします。 。

長方形の底面の周囲長 (P) = 4 つの辺の合計 = 2 (l + w)

長方形の底面の面積(A) = 長さ × 幅 = l × w

直角柱の側表面積の一般式は L.S.A. = PH であることがわかっています。ここで、P は底面周囲長、A は底面面積です。

一般式のすべての値を代入すると、次のようになります。 、

直方体の側面積 = 2h(l + w) 平方単位

どこ、

lは長さです

wは幅です

hは身長です

直角柱の総表面積の一般式は T.S.A. = PH+2A であることがわかっています。ここで、P は底面の周囲長、A は底面面積、H は角柱の高さです。

一般式のすべての値を代入すると、次のようになります。

直方体の全表面積 = 2h(l + w) + 2(l × w)

= 2 lh + 2 wh + 2 lw

直方体の全表面積 = 2 (lh + wh + lw) 平方単位

どこ、

lは長さです

wは幅です

hは身長です

角柱

底面が正方形のプリズムを正方プリズムといいます。四角柱は、4 つの長方形の面と 2 つの平行な正方形の底面で構成されます。プリズムの高さを h、正方形の底辺の長さを s とします。

正方形の底辺の周囲長 (P) = 4 つの辺の合計 = s + s + s + s = 4s

正方形の底辺の面積（A）＝（辺の長さ）²= s²

直角柱の側表面積の一般式は L.S.A. = PH であることがわかっています。ここで、P は底面周囲長、A は底面面積です。

得られた一般式にすべての値を代入すると、

四角柱の側表面積 = 4sh 平方単位

どこ、

sは正方形の底辺の辺です

hは四角柱の高さです

直角柱の総表面積の一般式は次のとおりであることがわかっています。 T.S.A. = PH+2A、 どこ P は底面周囲長、A は底面面積、H はプリズムの高さです。

一般式のすべての値を代入すると、次のようになります。

四角柱の総表面積 = [4sh + 2s ² ] 平方単位

どこ、

sは正方形の底辺の辺です

hは四角柱の高さです

五角柱

底面が５角形のプリズムをペンタプリズムといいます。五角柱は、5 つの傾斜した長方形の面と 2 つの平行な五角形の底面で構成されます。 h を五角柱の高さとします。 a と b は五角形の底辺の長さと辺の長さです。

五角形の底辺の周囲長(P) = 5つの辺の合計 = 5b

五角形の底辺の面積（A）＝5/2×（辺の長さ）×（辺の長さ）＝5ab

直角柱の側表面積の一般式は L.S.A. = PH であることがわかっています。ここで、P は底面周囲長、A は底面面積です。

得られた一般式にすべての値を代入すると、

五角柱の側表面積 = 5bh 平方単位

どこ、

bは五角形の底辺の辺です

hは五角柱の高さです

直角柱の総表面積の一般式は T.S.A. = PH+2A であることがわかっています。ここで、P は底面の周囲長、A は底面面積、H は角柱の高さです。

得られた一般式にすべての値を代入すると、

五角柱の総表面積 = [5bh + 5ab] 平方単位

どこ、

bは五角形の底辺の辺です
メール

a はアポセム長です。

hは五角柱の高さです

六角柱

底辺が六角形の角柱を六角柱といいます。六角柱は、6 つの傾斜した長方形の面と 2 つの平行な六角形の底面で構成されます。 h を六角柱の高さとします。 aは六角形の底辺の辺の長さです。

六角形の底辺の周長（P）＝6辺の和＝6a

六角形の底辺の面積（A）＝6×（正三角形の面積）

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

直角柱の側表面積の一般式は L.S.A. = PH であることがわかっています。ここで、P は底面周囲長、A は底面面積です。

得られた一般式にすべての値を代入すると、

六角柱の側表面積 = 6ah 平方単位

どこ、

aは六角形の底面の辺です

hは六角底の高さです

直角柱の総表面積の一般式は T.S.A. = PH+2A であることがわかっています。ここで、P は底面の周囲長、A は底面面積、H は角柱の高さです。

一般式のすべての値を代入すると、次のようになります。

六角柱の全表面積 = [6ah +3√3a²] 平方単位

どこ、

aは六角形の底面の辺です

h は六角形の底面の高さです。