数学における台形: 台形は 4 つの辺を持つ多角形、つまり四角形です。トラペジウムの語源はギリシャ語でテーブルを意味するtrapezeです。複雑な四角形です。台形は、平行な辺が 1 組だけある特殊な四角形です。台形は、表のように表示される 2 次元の形状です。
台形には 4 つの辺と 4 つの頂点があります。私たちは台形の形を日常生活で目にしており、最も一般的な形の 1 つです。この記事では、について学びます 数学における台形とは何か、その性質、公式、例、台形の種類、およびその解決例をいくつか示します。
目次
数学における台形とは何ですか?
台形は、一対の平行な対辺を有する閉じた形状の 2 次元の四角形です。台形の平行な辺は底面と呼ばれ、台形の非平行な辺は脚と呼ばれます。台形には 4 つの辺と 4 つの角があります。あ 平行四辺形 2 つの平行な辺を持つ台形とも呼ばれます。
台形の定義
台形は、少なくとも 1 組の平行な辺を持つ四角形 (4 辺の多角形) です。これらの平行な辺は台形の底辺と呼ばれ、他の 2 つの辺は脚と呼ばれますが、必ずしも平行である必要はありません。
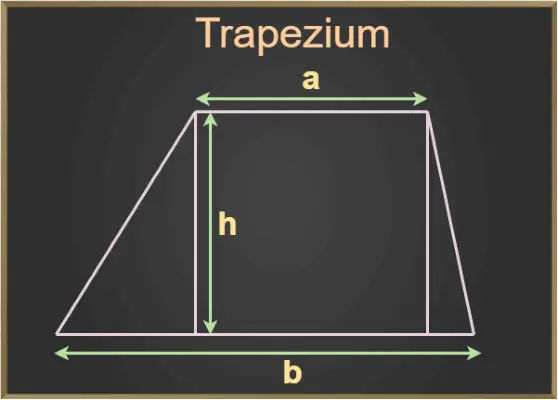
上の図では、a と b は台形の底辺、h は台形の高さです。
台形の形状
トラペジウムは、 四角形 つまり、4 つの辺を持つ多角形です。台形には 4 つの辺があり、一対の対向する辺が互いに平行です。台形の形は非常に一般的であり、日常生活の中で台形に似たさまざまなものを目にします。私たちが観察した台形の実際の例には、台形の形をしたテーブル、タイル、絵画などがあります。
台形の種類
辺と角度に基づいて、台形には 3 つのタイプがあります。
- 不等辺台形
- 二等辺台形
- 右台形

二等辺台形
脚の長さが等しい台形は二等辺台形と呼ばれます。つまり、二等辺台形では、平行でない 2 つの辺が等しいことになります。
Javaの配列
不等辺台形
すべての辺が等しくない台形を不等辺台形といいます。不等辺台形では、等しい角度は 2 つありません。
右台形
互いに隣接する直角のペアを持つ台形は、直角台形として知られています。
不規則な台形
台形には 1 組の平行な辺があり、他の 2 つの辺は平行ではありません。規則的な台形では、他の 2 つの非平行な辺は等しいですが、不規則な台形の場合、2 つの非平行な対向する辺は等しくありません。
台形の性質
台形にはさまざまなプロパティがあり、そのうちのいくつかは次のとおりです。
- 平行な辺: 台形には底辺と呼ばれる 2 つの平行な辺があります。 例: 図に示すように、辺 AB と辺 CD は互いに平行です。
- 非平行な辺: 台形の非平行な辺は脚と呼ばれますが、台形の脚の長さは等しくありません。 例: 辺 AD と辺 BC は、台形の非平行な辺です。
- 高度または高度: 底辺間の垂直距離は、台形の高さまたは高度と呼ばれます。上の図では、h は台形の高さです。
- 角度の合計
- 台形の隣接する内角の合計は 180°になります。 例: 共内角は 2 組あります。 1 つのペアは ∠ A と ∠ D で、もう 1 つのペアは ∠ B と ∠ C です。各ペアの共内角の合計は 180 です。°。
- 台形内のすべての内角の合計は常に 360° になります。 例 : 図中、∠A+∠D は 180°、∠B+∠C は 180°です。したがって、∠A+∠D +∠B+∠C = 360°となります。
- 中央値: 台形の中央値は、脚の中点を結ぶ線分です。中央値は塩基に平行であり、その長さは塩基の長さの平均です。
- 台形には、平行な対辺が 1 組だけあります。
台形フォーミュラ
台形の重要な公式は次のとおりです。
- 台形の面積 = 1/2 (平行辺の合計) × (平行辺間の距離)
- 台形の周囲 = 4 つの辺の合計
台形の公式の面積
台形には 2 つの平行な辺 a と b ユニットがあり、その高さは h です。
台形の面積は、底辺の平均を求め、その結果に標高を掛けることで計算できるようになりました。したがって、
台形の面積 = ((a + b)/2) × h
どこ、
- ある そして b 台形の底辺です
- h 高度です
二等辺台形の面積
a と b を台形 ABCD の平行な辺の長さとします。ここで、a と b は台形の底辺であり、a>b です。
さて、これは二等辺台形なので、c は 2 つの非平行な辺の長さ、h は台形の高さです。
ここで、AB = a、CD = b、BC = AD = c
で 直角三角形 、AED
垂線の長さ、 h = √(c 2 – (a-b) 2 ) [使用して ピタゴラスの定理 ]….(1)
今、
面積 = 1/2 × 平行辺の合計 × 台形の高さ
面積 = 1/2 × (a+b) × h
式 (1) を使用する
二等辺台形の面積 = 1/2 × [√(c 2 – (a-b) 2 ) (a+b)]
台形の外周公式
台形の周囲長は、すべての辺の合計を計算して求められます。したがって、
台形の周囲長 = AB + BC + CD + AD
どこ、 AB、BC、CD そして 広告 台形の辺です
二等辺台形の周囲
二等辺台形の a と b が平行な辺、つまり底辺の長さで、c が 2 つの等しい非平行な辺の長さである場合、周囲長は次の式で求められます。
周長 = a + b + 2c
どこ、
- ある 、 b 台形の底辺です
- c 台形の等しい辺です
台形と台形の違い
一般的には、台形と台形はどちらも同じですが、違いは原産国にあります。
- 台形 これは英国起源で、4 辺の多角形であり、互いに向かい合う平行な辺が 1 対あるだけの 2 次元図形です。インドではイギリス英語に従っているため、Trapezium という言葉が使用されます。
- 台形 これはアメリカ起源で、互いに向かい合う 1 組の平行な辺を持つ 4 辺の多角形でもあります。平行な辺は台形の底辺であり、別の 2 つの非平行な辺は台形の脚と呼ばれます。
台形の角度
台形は四角形であり、四角形のすべての角度の合計は 360 度です。したがって、台形の内角の合計は 360 度になります。
任意の正台形、つまり非平行な辺が平行線と非平行線の間に形成される隣接角度に等しい台形は等しい。したがって、これら 2 つの角度の合計は補足的です。
二等辺台形 ABCD のこの概念をサポートする例を考えてみましょう。AB が CD に平行で、AD が CD に等しい場合、∠A = ∠B および ∠C = ∠D であることがわかります。
∠A + ∠B + ∠C + ∠D = 360°
ここで、∠A = ∠B および ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
同様に、(∠B + ∠D) = 180°
台形の対角線
台形は特殊なタイプの四角形です。したがって、台形にも 2 つの対角線があります。長方形や平行四辺形などの他の四角形とは異なり、台形の対角線は同じ長さではありません。台形の対角線の長さは均等ではなく、台形の底辺の長さと角度によって異なります。
例: 二等辺台形 ABCD の場合、底角 ∠A が 80° である場合、もう一方の角 ∠C を求めます。
二等辺台形 ABCD の場合、
(∠A + ∠C) = 180°
gimpの色変更∠A = 80°とすると、
さて、80° + ∠C = 180°
∠C = 180 – 80
∠℃ = 100°
したがって、必要な角度∠Cは100°です。
台形の公式 – 台形の面積と周囲長
台形に関連する公式を次の表にまとめます。
| 財産 | 式 |
|---|---|
| エリア | 1/2×( ある + b )× h |
| エリア(二等辺台形) | 1/2 × [√(c2– (a-b)2) (a+b)] |
| 外周 | ある + b + c + d |
| 周囲 (二等辺台形) | ある + b +2 c |
| 中央値 | ( + b)/2 |
他の人はこちらも読んでいます:
- ひし形
- 三角形
- 台形の面積を求める公式とは何ですか?
台形の例
例 1: 他の 3 辺が 8 cm、12 cm、16 cm、周囲が 40 cm である場合、台形の 4 番目の辺を求めます。
解決:
周囲の長さは、すべての辺の合計として与えられます。未知の長さを「x」単位とする。
外周 = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4cm
したがって、未知の辺の長さは 4 cm です
例 2: 台形には長さ 15 cm と 11 cm の平行な辺と、それぞれ長さ 5 cm の非平行な辺があります。の周囲長を計算します。 台形。
解決:
これは、長さ 5 cm の非平行な辺が等しいことが明確に述べられているため、二等辺台形です。
二等辺台形によると、台形の平行でない 2 つの辺の長さが等しい場合、それは二等辺台形として知られます。
考えると、
- a = 15cm
- b = 11cm
- c = 5cm
周長 = a + b + 2c
キツネとオオカミの違いP = 15 + 11 + 2(5)
P = 15 + 11 + 10
P=36cm
例 3: 辺が 12 cm、14 cm、16 cm、18 cm の台形の周囲を求めます。
解決:
P = すべての辺の合計
選択範囲の並べ替えP = 12 + 14 + 16 + 18
P=60cm
よって、台形の周囲は60cmとなります。
例 4: 平行な辺の合計が 60 cm、高さが 10 cm の台形の面積を求めます。
解決:
考えると、
- 平行辺の合計 60cm
- 高さ、h = 10 cm
台形の面積、A = 1/2 × 平行な辺の合計 × 平行な辺間の距離
与えられた値を代入すると、
A =1/2×60×10
A = 30×10
A = 300cm2
したがって、台形の面積 = 300 cm2
数学の台形に関する練習問題
1. 底辺10cmと15cm、高さ6cmの台形の面積を求めます。
2. 台形の面積は 54 平方メートルです。一方のベースの長さが 12 メートル、高さが 6 メートルの場合、もう一方のベースの長さを求めます。
3. 底辺が 8 cm と 14 cm、非平行な辺が 5 cm と 7 cm の台形の周囲長を計算します。
4. 底辺が 18 cm と 30 cm になる台形の中央セグメントの長さを決定します。
5. 二等辺台形では、1 つの底辺の角度はそれぞれ 45 度です。もう一方の底辺の角度の測定値を求めます。台形が右台形ではないと仮定します。
要約 – 数学における台形
台形は 4 辺の多角形、または四角形であり、底辺と呼ばれる 1 対の平行な辺を持ち、脚と呼ばれる他の 2 つの辺は平行ではないことを特徴とします。テーブルなどの日常的なオブジェクトによく見られる台形は、その幾何学的特性で注目に値します。台形には、底辺間の垂直距離である高さと、非平行な辺の中点を接続し底辺に平行な中央線があります。
台形の面積は、底辺の長さを平均して高さを掛けることによって計算され、周囲長はすべての辺の合計になります。不等辺三角形、二等辺三角形、直角台形などのさまざまな分類があり、それぞれに固有の辺と角度の特性があるため、台形は実際の応用と幾何学的理論の両方で基本となります。
数学の台形に関するよくある質問
台形形状とは何ですか?
台形は、一対の線が常に平行である四角形です。テーブルの形に似ています。その名前は、テーブルを意味するギリシャ語のtrapezeから取られています。
台形の種類は何種類ありますか?
トラペジウムには2種類あり、
- 通常の台形: ここで、他の線のペアは等しい。
- 不規則な台形: この場合、他の線のペアは等しくありません。
台形には平行な辺がいくつありますか?
台形は 1 対の平行な辺を持つ四角形であることがわかります。したがって、台形には一対の平行な線(辺)があります。
台形は四角形とみなせますか?
A には 4 つの辺、4 つの頂点、4 つの角があります。したがって、台形の 4 つの内角すべての合計は 360 度である四角形と考えることができます。
正方形は台形と呼べるでしょうか?
台形は、平行な辺が 1 組のみあり、他の 2 つの辺は平行ではない四角形です。しかし、正方形の場合、平行な辺が 2 組あるため、台形とは見なされません。
台形の対角線は常に等しいですか?
台形の対角線は等しくない場合があります。正多角形の場合、対角線は等しいですが、不規則多角形の場合はそうではありません。
台形の性質とは何ですか?
トラペジウムの 5 つの特性は次のとおりです。
- 台形では、底辺は互いに平行です。
- 台形には追加の隣接する角があります。
- 対辺のうち 1 組のみが平行です。
- 台形内のすべての内角の合計は常に 360° になります。
- 平行でない辺の中点を結ぶ線は常に底辺と平行になります。
