三角柱の体積公式

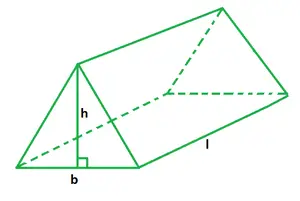
プリズムは、2 つの同一の端を持つ 3 次元の立体図形です。それは平らな側面、同様の底面、および等しい断面で構成されています。その面は底辺のない平行四辺形または長方形です。このように、3 つの長方形の面と 2 つの平行な三角形の底面をもつプリズムを三角プリズムと呼びます。三角形の底面は、互いに平行な側面によって接続されています。

三角柱の体積は、三角柱の内部の空間、または三角柱によって満たされる空間として定義されます。三角柱の底面積と高さがわかれば、その体積を計算できます。三角柱の体積は、底面の面積と角柱の高さ (角柱の長さとも呼ばれます) の積に等しくなります。三角柱の底面積は、三角形の底辺とその高度の積の半分に等しくなります。

式

V = (1/2) × b × h × l

どこ、

b は三角形の底辺、

h はプリズムの高度、

lはプリズムの長さです。

サンプル問題

問題1. 底辺6cm、高さ8cm、長さ12cmの三角柱の体積を求めよ。

解決：

b = 6、h = 8、l = 12 となります。
Java正規表現で

私たちが持っている公式を使用すると、

V = (1/2) × b × h × l

= (1/2) × 6 × 8 × 12

= 3 × 8 × 12

= 288立法。 cm

問題2. 底辺5cm、高さ7cm、長さ8cmの三角柱の体積を求めよ。

解決：

b = 5、h = 7、l = 8 となります。

私たちが持っている公式を使用すると、

V = (1/2) × b × h × l

= (1/2) × 5 × 7 × 8

= 5 × 7 × 4

= 140立方メートル。 cm
コンピュータの種類

問題 3. 底辺が 6 cm、高度が 9 cm、体積が 98 立方体の場合、三角柱の長さを求めてください。 cm。

解決：

b = 6、h = 9、V = 98 となります。

私たちが持っている公式を使用すると、

V = (1/2) × b × h × l

=> 98 = (1/2) × 6 × 9 × l
Javaの期間

=> 196 = 27リットル

=> l = 196/27

=> 長さ = 7.25 cm

問題 4. 底辺が 8 cm、長さが 14 cm、体積が 504 cu の場合、三角柱の高度を求めてください。 cm。

解決：

b = 8、l = 14、V = 504 となります。

私たちが持っている公式を使用すると、

V = (1/2) × b × h × l

=> 504 = (1/2) × 8 × h × 14

=> 504 = 56時間
抽象クラス

=> h = 504/56

=> 高さ = 9 cm

問題5. 長さ18cm、高さ10cm、体積450立方体の三角柱の底面の面積を求めよ。 cm。

解決：

l = 18、h = 10、V = 450 となります。

我々が持っている体積の公式を使用すると、

V = (1/2) × b × h × l

=> 450 = (1/2) × b × 10 × 18

=> 450 = 90b

=> b = 450/90

=> b = 5 cm

したがって、三角形の底辺の面積は、

A = (1/2) × b × h

= (1/2) × 5 × 10

= 25平方センチメートル