数学は、幅広い概念と原則から構成される魅力的な科目です。そのような概念の 1 つが 指数表記 。指数表記は、基数を特定の累乗 (または指数) にする基本的な概念であり、巨大な数や最小の数をより適切に表現するために使用される強力な概念です。この記事では、そのような例の 1 つ、つまり 10 から 5 について説明します。^番目力。そこで、この記事では、指数表記の概念を知り、10 から 5 までの重要性について説明します。^番目パワー、この値を表現するさまざまな方法について学び、数学以外のさまざまな分野での指数表記の応用について話し合います。

指数表記の定義

指数表記または科学表記は、数値を表すための標準化され体系化された方法を提供します。膨大な数や小さな数を扱う場合、表現が簡素化され明瞭さが増すため、有益です。

科学表記法の一部

この表記には 2 つの部分があります。

1. 基数
2. 指数（または累乗）数

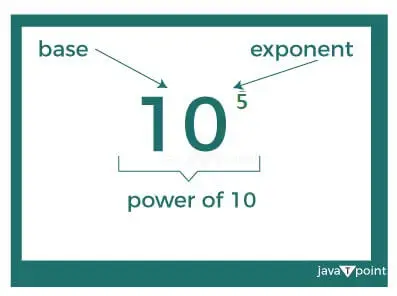
底は 10、指数は 5 です。これは、底の数値 (10) が何倍になるかを示します。これはつまり 10 の 5 乗は、10 を 5 回乗算したものに相当します。 。

10 x 10 x 10 x 10 x 10 = 10 を意味します。⁵

10を5まで表現する^番目力

10 の 5 乗を表現または表す方法はたくさんありますが、それが使用される分野や個人の好みによっても異なります。

科学表記:最も単純な表現は 10 です⁵、10 は基数、5 は指数またはべき乗です。この形式は通常は理解可能であり、数学や科学の文献で一般的に使用されています。数値表現:10 の 5 乗を表すもう 1 つの方法は、数値を拡張形式で 100,000 と書くことです。この形式は、数値を桁に分解し、その重要性を理解するためにその大きさを強調表示します。長い形式：10 の 5 乗を長い形式で表すと「10 万」になります。私たちは日常言語でこ​​の形式を使用するため、数字をより簡単に理解できます。

重要な

10から5まで^番目電力は、主に科学研究、テクノロジー、日常生活など、さまざまな分野で非常に重要です。これは 100,000 の値を表し、1 にゼロが 5 つ続きます (つまり 100,000)。科学表記法では、この値は、惑星と天体の間の距離、宇宙の星の数、世界の人口など、膨大な量を測定するときによく使用されます。これにより、科学者や研究者はこれらの非常に大量の量をより簡単に表現できるようになり、データの理解と分析が容易になります。

10から5までの応用^番目力

計算を理解したところで、10 と 5 の関連性を見つけることができるいくつかの実際的なアプリケーションを検討してみましょう。^番目力：

デジタル技術：コンピューターやデジタル テクノロジーでは、10 の累乗が重要な役割を果たします。コンピュータは、2 桁体系 (0 と 1) に基づくバイナリ コードを使用して情報を保存および処理します。 2 のべき乗は、10 のべき乗と密接に関係しており、メモリ カードのサイズ、データ転送速度、プロセッサの速度を表すために使用されます。人口増加：指数関数的な増加は、人口増加などの自然現象で頻繁に観察されます。 10対5のコンセプト^番目電力は、時間の経過とともに人口がどのように急速に増加するかを理解するのに役立ちます。たとえば、100,000 人の人口が年間 10% の割合で増加すると、4 年後には約 14,6410 人に達します。科学表記:10から5まで^番目検出力は科学的記数法の重要な要素です。この表記法は、非常に大きな数値または最小の数値を、より管理しやすい形式で表現します。スケールと大きさ:10 の累乗は、物体や現象の広大さまたは微細さを説明するためによく使用されます。たとえば、天文学者は、光が 1 年間に移動する距離である光年の概念を使用します。大きな数値を計算する:金融、物理学、工学などの分野では、通常、大規模な数値計算が必要になります。指数表記はコンパクトな表現を可能にし、エラーの可能性を減らすため、これらの計算を簡素化するのに役立ちます。

結論

べき乗を理解することは、さまざまなべき乗の数値を表現するために不可欠なスキルです。この記事では、10 を 5 で表現する方法を検討しました。^番目べき乗、これは 10 を 5 回掛けることを意味します。結果の 100,000 は、科学的表記法、変換単位、2 進数システムなど、さまざまなコンテキストで現れる基本的な値です。指数表記の概念とその実践的な応用を知ることで、日常生活における数学の力と豊かさ（存在感）をより深く理解することができます。