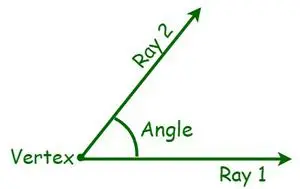
幾何学において、角度は幾何学的形状の重要な測定値です。角度は、一方を他方に対応させるために必要な 2 つの線または平面の交点を中心とした回転角度として定義されます。角度の測定に基づいて、さまざまな種類の角度があります。度またはラジアンで測定されます。角度は、頂点と呼ばれる共通点から発散する 2 本の線または光線によって形成される形状です。 2 本の光線が交差するとき、つまり、半線が共通の端点で投影されるとき、角度が形成されます。現在、共通の端点は頂点と呼ばれ、光線はアームと呼ばれます。
角度の種類

- 鋭角: 鋭角とは、0 度より大きく 90 度未満の角度です。つまり、その範囲は 0 ° から 90 ° (両方を除きます) です。
- 直角: 直角とは、正確に 90 度を測定する角度を指します。
- 鈍角: 鈍角とは、90 度より大きく 180 度未満の角度です。つまり、90 度から 180 度までの範囲になります (両方を除きます)。
- 直角: 直角とは、正確に 180 度の角度を指します。
- 反射角: 反射角は 180 度を超え 360 度未満の角度です。つまり、180 度から 360 度までの範囲になります (両方を排他的)。
- 完全な角度または完全な回転: 完全な角度は、正確に 360 度を測定する角度と呼ばれます。
補角、補角、隣接角、非隣接角など、他のタイプの角度もあります。
- 補角: 2 つの角度の合計が直角、つまり 90° である場合、それらの角度は相補的であると言われます。
- 補助角度: 2 つの角度の合計が 180° に等しい場合、それらの角度は補足的であると言われます。
- 隣接する角度: 2 つの角が共通の頂点と共通のアームを共有している場合、それらの角は隣接していると言われます。
- 隣接しない角度: 2 つの角は、共通の頂点と共通のアームを共有していない場合、隣接していないと言われます。
角度を求める公式
角度を求める公式にはさまざまな種類があります。それらの中には、中心角の公式、2倍角の公式、半角の公式、複角の公式、内角の公式などがあります。
- 中心角の公式を使用して、円で作られた線分の角度を決定します。
- 内角の和の公式を使用して、多角形の不足している角度を決定します。
- 直角三角形の欠けている角度を見つけるには三角比を使用します。
- サインの法則またはコサインの法則を使用して、直角でない三角形の不足している角度を見つけます。
式の名前 | 式 | 未知の角度を見つけるにはどうすればよいですか? |
|---|---|---|
| 中心角の公式 .netチュートリアル | θ =(s × 360°)/2prここで、s は円弧の長さ、r は円の半径です。 | 円弧の長さと円の半径の値を代入して、円に作られる線分の角度を決定します。 |
| 内角の和の公式 | 180°(n-2)ここで、n は多角形の辺の数です。 | 多角形の未知の内角を決定するには、まずこの公式を使用してすべての内角の合計を計算し、次にその結果からすべての既知の角度の合計を減算します。 |
| 三角比 | sinθ = 反対側/斜辺cos θ = 隣接辺/斜辺Tanθ = 反対側/隣接側 | 直角三角形の利用可能な 2 つの辺に応じて、これらの三角比のいずれかを選択して未知の角度を見つけます。 |
| 正弦の法則 | a/sin A = b/sin B = c/sin Cここで、A、B、C は三角形の内角、a、b、c はそれぞれの対辺です。 | 2 つの辺と含まれない角度 (または) 2 つの角と含まれない辺がわかっている場合、正弦の法則を使用して三角形の未知の角度を決定できます。 |
| 余弦の法則 | ある2= b2+c2– 2bc cos Ab2= c2+a2– 2ca cos Bc2= a2+b2– 2ab cos Cここで、A、B、C は三角形の内角、a、b、c はそれぞれの対辺です。 | 3 つの辺 (または) 2 つの辺と夾角がわかっている場合、余弦の法則を使用して三角形の未知の角度を決定できます。 |
質問例
質問 1: 角度を求める三角関数の公式の 1 つを使用して、指定された三角形の頂点 B の角度を求めます。

解決:
考えると、
BC = 3 単位 = θ の隣接辺。
AC = 4 単位 = θ の反対側。
この場合、θ の反対側と隣接する側の両方がわかります。したがって、タンジェントの公式を使用して θ を求めることができます。
⇒tanθ=反対側/隣接側
⇒tanθ=4/3
プレオーダートラバーサル⇒ θ = タン-1(4/3) ⇒ θ = 53.1°
したがって、頂点 B の角度は 53.1° になります。
質問 2: ∠Z = 35°、x = 3 インチ、y = 8 インチ、z = 3.5 インチの場合、頂点 X と Y の角度を求めます。

解決:
考えると、
∠Z = 35°、x = 6 インチ、y = 3 インチ、z = 3.5 インチ
3 つの辺と角度がすべてわかっているので、正弦定規の公式を使用できます。
正弦則の公式から、次のようになります。
x/sin X = y/sin Y = z/sin Z
今、
y/sin Y = z/sin Z
⇒ 3/sin Y = 3.5/sin 35°
⇒ 3/Y なし = 3.5/0.574 {したがって、sin 35° = 0.574}
⇒ sin Y = 3 × (0.574/3.5) = 0.492
⇒ ∠Y = 罪−1(0.492) = 29.47°
三角形の 3 つの角度の合計は 180° であることがわかります。
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29.47° + 35° = 180°
⇒ ∠X = 180° – 64.47° = 115.53°
したがって、∠X = 115.53°、∠Y = 29.47°となります。
質問 3: 五角形の内角のうち 4 つが 110°、85°、136°、105° である場合、その 5 番目の内角を計算してください。
バイナリツリーとBSTの比較
解決:
五角形の辺の数 (n) = 5。
さて、五角形の 5 つの内角すべての合計 = 180 (n -2)°
= 180 (5 – 2)° = 540°。
指定された 4 つの内角の合計 = 110°+ 85°+ 136°+ および 105°= 436°。
したがって、5 番目の内角 = 540° – 436° = 104°
したがって、五角形の 5 番目の内角は 104° です。
質問 4: y の値と、指定された図の角度の尺度を決定します。

解決:
与えられた図から、(4y – 6)° と (3y + 5)° が補角であることがわかります。つまり、(4y – 6)° と (3y + 5)° の合計は 90 です。 °。
⇒ (4y – 6)° + (3y + 5)° = 90°
すべて置き換える⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
ここで、(4y – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
質問 5: 角度を求める公式の 1 つを使用して、指定された三角形の頂点 Q の角度を求めます。

解決:
p = QR = 6 cm、q = PR = 9 cm、r = PQ = 7 cmと仮定します。
3 つの辺と角度がすべてわかっているので、コサイン則の公式を使用して角度の頂点 Q を見つけることができます。
⇒ q2= p2+r2– 2PRコスQ
⇒ 92= 62+72– 2(6)(7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
客観的なJava⇒ 81 = 85 – 84cos Q
⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92.72°
したがって、頂点 Q での角度、∠Q = 92.72°になります。
問題 6: 円弧の長さが 12π、半径が 9 cm の場合、円に作られる線分の角度を計算してください。
解決:
考えると、
円弧の長さ = 12π
半径 (r) = 9 cm
さて、角度の公式は次のようになります。
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
したがって、角度は240°になります。
