挿入ソートと選択ソートは 2 つの一般的なソート アルゴリズムであり、それらの主な違いは、ソートされたシーケンス内で要素を選択して配置する方法にあります。
選択の並べ替え:
- 選択ソートでは、入力配列はソートされた部分とソートされていない部分の 2 つの部分に分割されます。
- このアルゴリズムは、未ソート部分の最小要素を繰り返し見つけて、それを未ソート部分の左端の要素と交換し、ソート済み部分を 1 要素ずつ拡張します。
- 選択ソートの時間計算量は、すべての場合で O(n^2) です。
挿入ソート:
- 挿入ソートでは、入力配列もソートされた部分とソートされていない部分の 2 つの部分に分割されます。
アルゴリズムは、ソートされていない部分から要素を取得し、それをソートされた部分の正しい位置に配置し、大きい要素を 1 つ右に移動します。
挿入ソートの時間計算量は最悪の場合でも O(n^2) ですが、部分的にソートされた配列ではパフォーマンスが向上し、最良の場合の時間計算量は O(n) になります。
主な違い: - 選択ソートでは、ソートされていない部分をスキャンして最小の要素を見つけます。一方、挿入ソートでは、ソートされた部分をスキャンして、要素を配置するための正しい位置を見つけます。
選択ソートでは、挿入ソートよりもスワップが少なくなりますが、より多くの比較が必要になります。
入力配列が部分的にソートされている場合、またはほぼソートされている場合は、挿入ソートの方が選択ソートより効率的ですが、配列が高度にソートされていない場合は、選択ソートのパフォーマンスが向上します。
要約すると、両方のアルゴリズムの時間計算量は同様ですが、選択方法と配置方法が異なります。どちらを選択するかは、入力データの特性と当面の問題の特定の要件によって異なります。
挿入ソートの利点:
- シンプルで理解しやすく、実装も簡単です。
- 小規模なデータ セットまたはほとんどソートされたデータの場合に効率的です。
- インプレース並べ替えアルゴリズム。つまり、追加のメモリは必要ありません。
- 安定した並べ替えアルゴリズム。つまり、入力配列内の等しい要素の相対的な順序が維持されます。
挿入ソートの欠点:
- 大規模なデータ セットや逆順序のデータの場合は非効率的であり、最悪の場合の時間計算量は O(n^2) になります。
- 挿入ソートには多くのスワップが含まれるため、最新のコンピューターでは速度が遅くなる可能性があります。
選択ソートの利点:
- シンプルで理解しやすく、実装も簡単です。
- 小規模なデータ セットまたはほとんどソートされたデータの場合に効率的です。
- インプレース並べ替えアルゴリズム。つまり、追加のメモリは必要ありません。
選択並べ替えの欠点:
- 大規模なデータ セットの場合は非効率的であり、最悪の場合の時間計算量は O(n^2) になります。
- 選択ソートには多くの比較が含まれるため、最新のコンピューターでは速度が遅くなる可能性があります。
- ソート アルゴリズムが不安定です。つまり、入力配列内の等しい要素の相対的な順序が維持されない可能性があります。
この記事では、挿入ソートと選択ソートの違いについて説明します。
挿入ソート は、手の中のトランプを並べ替えるのと同じように機能するシンプルな並べ替えアルゴリズムです。配列は仮想的にソートされた部分とソートされていない部分に分割されます。ソートされていない部分の値が選択され、ソートされた部分の正しい位置に配置されます。
アルゴリズム:
サイズ n の配列を昇順に並べ替えるには、次のようにします。
- 配列に対して arr[1] から arr[n] までを繰り返します。
- 現在の要素 (キー) をその前の要素と比較します。
- キー要素がその前の要素より小さい場合は、前の要素と比較します。大きい要素を 1 つ上の位置に移動して、交換された要素用のスペースを確保します。
以下は、挿入ソートを示す画像です。
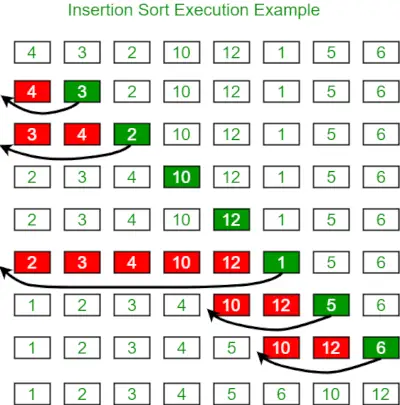
以下は同じプログラムです。
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j - 1; arr[j + 1] = キー; } } // サイズ N の配列を出力する関数 void printArray(int arr[], int n) { int i; // 配列を出力します (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
ジャワ
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j - 1; arr[j + 1] = キー; } } // サイズ N の配列を出力する関数 static void printArray(int arr[], int n) { int i; // 配列を出力します (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // ドライバー コード public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; int N = arr.length; // 関数呼び出し printArray(arr, N);このコードは code_hunt によって提供されています。 |
>
# Python 3 program for the insertion sort># Function to sort an array using># insertion sort>def>insertionSort(arr, n):>>i>=>0>>key>=>0>>j>=>0>>for>i>in>range>(>1>,n,>1>):>>key>=>arr[i]>>j>=>i>->1>># Move elements of arr[0..i-1],>># that are greater than key to>># one position ahead of their>># current position>>while>(j>>>=>0>and>arr[j]>キー):>>arr[j> +>1>]>=>arr[j]>>j>=>j>->1>>arr[j>+>1>]>=>key># Function to print an array of size N>def>printArray(arr, n):>>i>=>0>># Print the array>>for>i>in>range>(n):>>print>(arr[i],end>=>' '>)>>print>(>' '>,end>=>'')># Driver Code>if>__name__>=>=>'__main__'>:>>arr>=>[>12>,>11>,>13>,>5>,>6>]>>N>=>len>(arr)>># Function Call>>insertionSort(arr, N)>>printArray(arr, N)>>># This code is contributed by bgangwar59.>>>C#
// C# program for the above approach>using>System;>class>GFG>{>>// Function to sort an array using>>// insertion sort>>static>void>insertionSort(>int>[] arr,>int>n)>>{>>int>i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j - 1; arr[j + 1] = キー; } } // サイズ N の配列を出力する関数 static void printArray(int[] arr, int n) { int i; // 配列を出力します (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // ドライバー コード static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; int N = arr.Length; // 関数呼び出し printArray(arr, N); Dharanendra L V による寄稿>>'>
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j - 1; arr[j + 1] = キー; } } // サイズ N の配列を出力する関数 function printArray(arr,n) { let i; // 配列を出力します (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // ドライバー コード let arr=[12, 11 , 13, 5, 6]; let N = arr.length; // 関数呼び出し insertSort(arr, N); // このコードは avanitrachhadiya2155 によって提供されています。>5 6 11 12 13> の 選択ソート このアルゴリズムは、ソートされていない部分から最小の要素 (昇順を考慮) を繰り返し見つけて先頭に置くことによって配列をソートします。このアルゴリズムは、指定された配列内に 2 つのサブ配列を維持します。
- 部分配列はすでにソートされています。
- 残りの部分配列はソートされていません。
選択ソートを繰り返すたびに、ソートされていない部分配列から最小要素 (昇順を考慮) が選択され、ソートされた部分配列に移動されます。
以下は、上記の手順を説明する例です。
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>以下は同じプログラムです。
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>ジャワ
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
配列リストから削除する
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>JavaScript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>出力:Sorted array: 11 12 22 25 64>挿入ソートと選択ソートの表形式の違い:
挿入ソート 選択範囲の並べ替え 1. 事前に並べ替えられた配列に値を挿入して、配列内の値のセットを並べ替えます。 リストから最小値/最大値を検索し、昇順/降順に並べ替えます。 2. 安定したソートアルゴリズムです。 これは不安定な並べ替えアルゴリズムです。 3. 配列がすでに昇順になっている場合、最良の場合の時間計算量は Ω(N) です。 Θ(N2)最悪の場合と平均的な場合。 最良のケース、最悪のケース、および平均的な選択ソートの場合、複雑さ Θ(N2)。 4. この並べ替えアルゴリズムで実行される比較操作の数は、実行される交換操作よりも少なくなります。 この並べ替えアルゴリズムで実行される比較操作の数は、実行される交換操作よりも多くなります。 5. 選択ソートよりも効率的です。 挿入ソートよりも効率が低くなります。 6. ここでは要素が事前にわかっているので、それらを配置するための正しい位置を検索します。 要素を配置する場所は事前にわかっているので、その位置に挿入する要素を検索します。 7。 挿入ソートは次の場合に使用されます。
- 配列の要素数が少ない
- 並べ替える要素がわずかに残っています
選択ソートは次の場合に使用されます。
- 小さなリストを並べ替える必要があります
- 交換費用は関係ない
- すべての要素のチェックは必須です
- メモリへの書き込みコストはフラッシュ メモリと同様に重要です (バブル ソートの O(n2) と比較して、スワップの数は O(n) です)
8. 挿入ソートは適応的です。つまり、すでに実質的にソートされているデータセットに対して効率的です。時間計算量は次のとおりです。 お(kn) 入力内の各要素が以下の場合 k ソートされた位置から離れた場所 選択ソートは、インプレース比較ソート アルゴリズムです。
