数量を表すために使用され、計算に使用される算術値は数値として定義されます。数字を表す4、5、6のような記号は数字として知られています。数字がなければ、物、日付、時間、お金などを数えることができません。これらの数字は、測定やラベル付けにも使用されます。
数値の特性により、数値に対する算術演算の実行に役立ちます。これらの数字は、数値形式でも単語でも書くことができます。
例えば , 3 は単語で 3 と書き、35 は単語で 35 と書きます。生徒は 1 から 100 までの数字を単語で書いて学習することができます。
さまざまな種類の数字があり、それを学ぶことができます。整数と自然数、奇数と偶数、有理数と無理数などです。
番号体系とは何ですか?
記数法は、数値または記号を数学的に使用して、特定のセットの数値を表す数学的方法である、数値を書くことによって示す方法です。数字や記号を使って論理的に数字を表すための表記法を数値体系と定義します。
0 から 9 までの数字を使用してすべての数字を形成できます。これらの数字を使えば、誰でも無限の数字を作り出すことができます。
たとえば、156、3907、3456、1298、784859 などです。
平方根とは何ですか?
平方根の数値。それ自体を乗算すると元の数値が得られます。 a が b の平方根であると仮定すると、a = √b と表されるか、同じ式を a2 = b と表すことができます。ここで、数値の根を表すために使用した「√」という記号を根号と呼びます。正の数をそれ自体で乗算する場合は、その数の 2 乗を表します。任意の正の数の二乗の平方根は、元の数を与えます。
例えば、 4の2乗は16,4です2= 16、および 16 の平方根、√16 = 4。4 は完全な平方であるため、そのような数値の平方根を求めるのは簡単ですが、不完全な平方の場合、それは非常に困難です。
平方根は次のように表されます。 「√」 それを根号記号といいます。この記号を使用して数値「a」を平方根として表すには、「√a」と書くことができます。ここで、a は数値です。
SQLをキャストする
ここで根号記号の下にある数値は、ラジカンドと呼ばれます。たとえば、4 の平方根は 4 の根号としても表されます。どちらも同じ値を表します。
平方根を求める公式は次のとおりです。 a = √b
平方根の性質
これは、正の数値を入力として受け取り、指定された入力数値の平方根を返す 1 対 1 の関数として定義されます。
f(x) = √x
たとえば、ここで x = 9 の場合、関数は出力値 3 を返します。
平方根の性質は次のとおりです。
- 数値が完全な平方数である場合、完全な平方根が確実に存在します。
- 数値が偶数のゼロ (0) で終わる場合、平方根を求めることができます。
- 2 つの平方根値を乗算することができます。たとえば、√3 に √2 を掛けると、結果は √6 になります。
- 2 つの同じ平方根を乗算すると、結果は根数になる必要があります。これは、結果が非平方根数であることを示しています。たとえば、√7 に √7 を掛けると、得られる結果は 7 になります。
- 負の数の平方根は定義されていません。したがって、完全二乗は負になることはできません。
- 一部の数値が 2、3、7、または 8 (単位の桁) で終わる場合、完全な平方根は存在しません。
- 一部の数値の単位桁が 1、4、5、6、または 9 で終わる場合、その数値は平方根になります。
完全二乗である数値の平方根を見つけるのは簡単です。
アメリカは都市はいくつありますか
完全正方形 は、数値自体の乗算として記述できる正の数です。または、完全二乗は、任意の整数の 2 乗の値である数値であると言えます。
2 つの等しい整数の積として表現できる数値。たとえば、16 は 2 つの等しい整数の積 (4 × 4 = 16) であるため完全平方です。ただし、24 は 2 つの等しい整数の積として表すことができないため、完全平方ではありません。 (8 × 3 = 24)。
整数を二乗して得られる数を完全二乗といいます。
N が整数 y の完全二乗であると仮定すると、これは N = y と y = y の積として書くことができます。2。
したがって、完全二乗公式は次のように表すことができます。
N = Y 2
値を含む数式を使用してみましょう:
y = 9、N = y の場合2
つまり、N = 92= 81。
ここで、81 は整数の 2 乗であるため、9 の完全 2 乗です。
平方根の助けを借りて、与えられた数値の平方根を計算すると、その数値が完全な平方であるかどうかを識別できます。
平方根が整数の場合、指定された数値は完全平方になり、平方根の値が整数でない場合、指定された数値は完全平方ではありません。
オブジェクトJavaとは何ですか
例えば、 24 が完全な平方であるかどうかを確認するには、その平方根を計算します。 √24 = 4.898979。ご覧のとおり、4.898979 は整数ではないため、24 は完全な平方ではありません。
別の例を挙げてみましょう
数字 49。√49 = 7。7 は整数であることがわかり、したがって 49 は完全平方です。
196は完全正方形ですか?
解決:
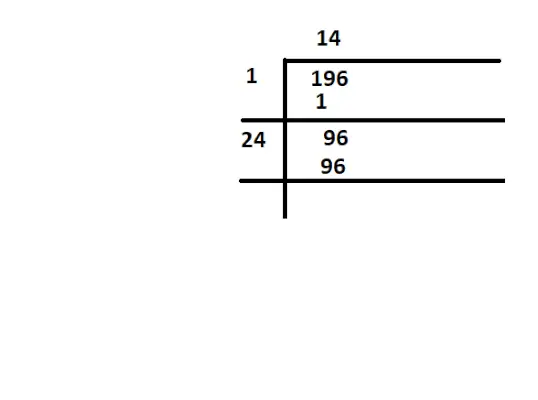
196 が完全な平方であるかどうかを確認するには、196 の平方根を見つける必要があります。
196 の完全平方
ここで、196の平方根は14です
Javaの同等のインターフェース完全二乗は、数値そのものの乗算として記述できる正の数です。または、完全二乗は、任意の整数の 2 乗の値である数値であると言えます。
ここで、√196 = 14 または 14 と書くことができます。2= 14 × 14 = 196。
したがって、196 は完全平方です。
同様の質問
質問 1: 625 の平方根は何ですか?
解決:
625 の完全二乗
アミシャ・パテルここで 625 は 25 の完全二乗です
したがって、√625 = 25 または 25 と書くことができます。2= 25 × 25 = 625
質問 2: 24 の平方根はどうやって求めますか?
解決:
24の平方根
ここで、24 は 4.8989 の完全な 2 乗ではありません。
したがって √24 = 4.8989..
質問 3: 361 の平方根を求めますか?
解決:
361の平方
ここで 361 の平方根は 19 です 、完全二乗である整数
したがって、√361 = 19 または 192= 19 × 19 = 361