類似項とは、同じ変数を同じべき乗した代数式内の項です。類似項と相違項は代数における項の種類であり、変数とその累乗をチェックするだけで類似項と相違項を区別できます。代数項を代数方程式から得られる個々の項として定義します。
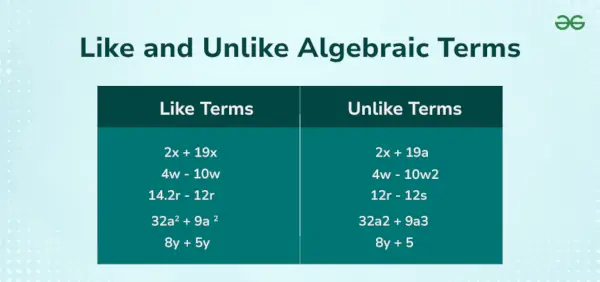
たとえば代数方程式では 5x + 3年 2 = 12 3 つの用語があります。 5x、3y²、 そして 12 。ここ、 5倍、 そして 3歳 2 は可変項、12 は定数項です。下の画像は、類似した用語と異なる用語を示しています。
この記事では、類似用語、相違用語、その例、簡略化などについて詳しく説明します。
類似条件
類似項とは、同じ変数を持ち、各変数の累乗も同じ項です。同様の項を組み合わせて代数式を簡略化することができ、これを非常に簡単に計算できます。たとえば、3y + 5y は、3y と 5y という同様の項を含む代数式です。この代数式を簡略化するために、同様の項を追加します。したがって、与えられた式の簡略化は 8y です。
類似用語の例
類似項とは、同様の検出力を持つ同じ変数を持つ項です。同様の用語の例としては、次のようなものがあります。
- 40xy 2 と56xy 2 : 最初の例では xy2は両方の項に共通の係数です。したがって、これらは用語のようなものです。
- 30z 2 と18z 2 : と2は両方の項に共通の係数です。したがって、これらは用語のようなものです。
- 45abc と 29abc: abc は両方の項に共通の係数です。したがって、これらは用語のようなものです。
- 18r 3 そして38r 3 : r3は両方の項に共通の係数です。したがって、これらは用語のようなものです。
- 2xy と 8xy: xy は両方の項に共通の係数です。したがって、これらは用語のようなものです。
類似用語の加算および減算
同様の項の加算と減算は簡単に実行でき、特別なルールは必要ありません。通常は通常の加算と減算のルールを使用して簡略化されます。この概念は、次の例を使用して理解できます。
例: 11x を簡略化する 3 +5倍 3
の Java インスタンス
解決:
ご覧のとおり、これらは同様の変数を持ち、検出力も一定であるため、類似した項となります。
これらの用語を直接簡単に追加できます。
= 11x3+5倍3
= 16x3
これが可能なのは、それらが同様のパワーを持つ同じ変数を持っているためであり、これはルピーにルピーを直接加算できる、つまり 5 R + 7 R は 12 R であると理解できます。ただし、ルピーとドルを直接加算することはできませんし、5 R + 7 ドルを直接単純化することもできません。
同様に、同様の項を直接減算したり、同様の項を追加したりすることもできます。これは次の例で理解できます。
クラスタリング
例 1: 11x を簡略化する 3 – 5倍 3
解決:
ご覧のとおり、これらは同様の変数を持ち、検出力も一定であるため、類似した項となります。
これらの項を直接減算することが簡単にできます。
= 11x3– 5倍3
= 6x3
例 2: 3 を追加します。 バツ +2 そして +5と4 バツ − 3 そして +7。
解決:
(3 バツ +2 そして + 5) + (4 バツ − 3 そして +7)
= (3 バツ + 4x) +(2y + (-3y))+ (5 + 7)
= 7 バツ − そして +12
規約とは異なります
用語とは異なり、異なる変数を含む用語であり、各変数には異なる指数が付いている場合と付いていない場合があります。たとえば、9x + 6y は、異なる項を含む代数式です。 2 つの異なる変数 x と y があるためです。
変数が異なる場合、項とは異なるため検出力はチェックしませんが、変数が同じ場合は、項に似ている場合と似ていない可能性があるため、検出力をチェックします。
5倍など2そして6倍2条件は似ていますが、5x2そして6倍3用語とは異なります。
異なる用語の例
項とは異なり、同じ変数も同様の検出力も持たない項です。異なる用語の例としては、次のようなものがあります。
- 40xy 2 および56xy: ここで、1 つの代数式では、変数は xy です。2もう 1 つの代数式では、変数は xy です。どちらの変数も同じですが、検出力が異なります。したがって、これらは用語とは異なります。
- 45abc と 29ab: ここで、一方の代数式では変数は abc であり、もう一方の代数式では変数は ab です。両方の変数は異なります。したがって、それらは用語とは異なるカテゴリに分類されます。
異なる用語の加算と減算
加算と減算は異項間では実行されません。つまり、異項間の加算や減算はできません。これは、6 kg の米に 5 リットルの牛乳を加算できないため、例から理解できます。同様に、用語とは異なり、足したり引いたりすることはできません。
たとえば、3xy + 5x はそれ以上解くことができず、同じままになります。
類似用語と非類似用語の違い
類似用語と非類似用語の違いについては、以下の表で説明します。
| 特徴 | 類似条件 | 規約とは異なります |
|---|---|---|
| 意味 Javaでリストを並べ替える | 類似用語とは、同じ変数を持つ用語です そして同じ指数値。 | 用語とは異なり、異なる変数を持つ用語です そして指数。 |
| 簡略化 | 同様の用語は簡単に簡略化できます。 | 簡略化できない用語とは異なります。 |
| 用語の結合 | 同様の項を直接組み合わせて計算することができます。 | 用語とは異なり、異なる量を表すため直接組み合わせることができません |
| 加算または減算 | 加算と減算は同様の条件で実行できます。 | 用語とは異なり、足したり引いたりすることはできません。 |
| 例 | 類似用語の例は、x です。2、5倍2、-11/3x2、など。 | 異なる用語の例は、x です。2そして、5倍3、-11/3xなど。 |
続きを読む
- 代数式
- 代数式の種類
似た代数項と異なる代数項の例
例 1: 3x、5xy、18x から似た用語と異なる用語を識別する 2 そして、5倍 3 、29xy、50x 3
解決:
指定された用語の「似ている」用語と「異なる」用語は次のとおりです。
類似条件: (5xy、29xy)、(5x)3、50倍3)
: Javaで規約とは異なります: 3倍、18倍2そして
例 2: 3xy + 5x を簡略化する 2 + 11ab – 4xy
解決:
与えられた式:3xy + 5x2+ 11ab – 4xy
指定された式の類似項、3xy および -4xy
単純化すると、
= 3xy – 4xy + 5x2+11ab
= -xy + 5x2+11ab
残りの項はすべて異なる項であるため、これ以上解くことはできません。
例 3: 8x + 15x を簡略化する 2 + 11x – 4x 2
解決:
指定された式: 8x + 15x2+ 11x – 4x2
指定された式の類似項、(8x, 11x) および (15x)2、-4x2)
単純化すると、
= 8x + 11x + 15x2– 4倍2
= 19x – 11x2
残りの項はすべて異なる項であるため、これ以上解くことはできません。
代数用語の似たものと異なるもの – FAQ
代数項とは何ですか?
代数項とは、代数方程式から得られる個々の項、つまり項を + や - などの演算記号で割ったものです。
メガバイトとギガバイトの違いは何ですか
類似用語と相違用語とは何ですか?
似た項と似ていない項は、代数式の項です。 「同様の」では、類似した変数があり、指数のべき乗は同じですが、「似ていない」では、変数とそのべき乗は異なります。
代数用語に似ている用語と異なる用語の違いは何ですか?
類似項と非類似項の基本的な違いは、類似項では同じべき乗を持つ同じ変数が存在するのに対し、非類似項では異なるべき乗を持つ異なる変数が存在することです。
代数項の類似項と相違項を見つける方法は?
類似項は、同じ変数と同じべき乗を持つ項であり、異なる項は、異なる変数と異なるべき乗を持つ項であり、変数を検査するだけで簡単に識別できます。
代数項のように足したり引いたりできるでしょうか?
5x や 11x などの類似項は簡単に加算または減算でき、16x として加算できます。
代数項と違って足したり引いたりできるのでしょうか?
2x や 3y などの用語と異なり、足したり引いたりすることはできません。したがって、異なる項を一緒に加算または減算することはできません。
