四分円 は、デカルト平面の 2 つの軸、つまり X 軸と Y 軸によって 4 つの等しい部分に分割される空間内の領域として定義されます。これら 2 つの軸は互いに 90 度で交差し、そのようにして形成される 4 つの領域は 4 象限、すなわち I 象限、II 象限、III 象限、IV 象限と呼ばれます。
Pythonソートタプル
この記事では、四分円とは何か、その面積、四分円グラフ、デカルト平面、四分円内の符号規則、横座標、座標、四分円上の点のプロットなど、四分円の重要な概念について説明します。
目次
グラフの象限とは何ですか?
象限とは、 デカルト平面 、X 軸と Y 軸の交差によって作成されます。この次元では、それぞれに固有の特性を持つ 4 つの象限が形成されます。右上の第 1 象限には、正の x 座標と y 座標があります。左上の第 2 象限には、負の x 座標と正の y 座標が含まれます。これらの象限を理解することは、グラフ上の点を見つけて解釈するために不可欠であり、デカルト座標をナビゲートして分析する体系的な方法を提供します。
座標平面上の 4 つの象限
X 軸と Y 軸で形成されるデカルト平面は 4 つの象限に分割され、それぞれに異なる特性があります。
- 第 1 象限: 右上に位置し、x 座標と y 座標は両方とも正です。この象限は、平面の右上部分の点を表します。
- 第二象限: 左上に位置し、x 座標は負、y 座標は正です。この象限は、平面の左上部分の点をカバーします。
- 第 3 象限: 左下に位置し、x 座標と y 座標は両方とも負です。平面の左下領域の点は、この象限に分類されます。
- 第 4 象限: 右下にあるように、x 座標は正、y 座標は負です。この象限には、平面の右下部分の点が含まれます。
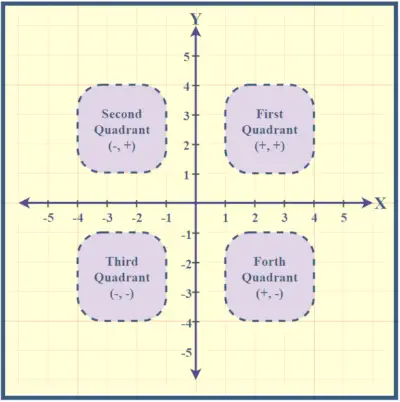
象限には、右上から反時計回りに番号が付けられます。 X 軸と Y 軸が交差する点は原点と呼ばれ、座標は (0,0) で、x と y の両方の値がゼロであることを示します。これらの象限を理解すると、デカルト平面内の点を見つけるのに役立ちます。
オリジンとは何ですか?
グラフ上の開始点は原点として知られ、(0, 0) として示され、水平 x 軸と垂直 y 軸が交差する場所です。これは、原点では x と y の値が両方とも 0 であることを意味します。これは、グラフ上の他の点を見つけるための参照点として機能します。上に追加された画像では、点 O が原点を示しています。
象限の横座標と縦座標
4 つの象限では、数値はペア (a, b) として表されます。「a」は x 座標を表し、「b」は y 座標を表します。プロットせずに点の位置を把握するには、x 座標 (横座標) と y 座標 (縦座標) の符号に注意してください。たとえば、Q (3, -5) のような点がある場合、符号 (+ve, -ve) はそれが象限 IV にあることを示します。
横軸は Y 軸からの水平距離を示します。正の横座標は右を意味し、この例では横座標 = 3 は原点から x 軸に沿って 3 単位右に進むことを意味します。
縦軸は原点からの垂直距離を示します。負の縦軸は、y 軸に沿って原点から下に行くことを意味します。この例では、縦座標 = -5 は 5 単位ずつ下がることを意味します。
象限における署名規約
象限内の記号規則は、以下に追加された画像を使用すると簡単に理解できます。

XY 平面では、x 軸に沿って左から右に移動すると、x 座標が増加します。同様に、y 軸に沿って下から上に移動すると、y 座標が増加します。 XY 平面は 4 つの象限に分割されており、それぞれに x 座標と y 座標の特定の符号規則があります。
| 四分円 | x座標 | y 座標 |
|---|---|---|
| 第 1 象限 | ポジティブ (+) | ポジティブ (+) |
| 第2象限 | ネガティブ (-) | ポジティブ (+) |
| 第3象限 | ネガティブ (-) | ネガティブ (-) |
| 第4象限 | ポジティブ (+) | ネガティブ (-) |
したがって、第 1 象限の点は x と y の両方が正の値を持ち、第 2 象限の点は負の x と正の y を持ち、第 3 象限は x と y の両方の値が負で、第 4 象限は正の x と y を持ちます。負の y。
象限上の点のプロット
デカルト平面では、点は x 軸と y 軸によって識別されます。これらの点は (a, b) として示されます。ここで、「a」は x 座標 (横座標)、「b」は y 座標 (縦座標) です。象限内に点を配置するには、これらの座標の符号を考慮します。 x と y の値は、点がそれぞれ x 軸と y 軸からどのくらい離れているかを表します。
たとえば、点 (2, -5) をデカルト平面上にプロットします。座標の符号を分析すると、その点が第 4 象限にあることがわかります。原点を参照点として使用し、X 軸から 2 単位 (右)、Y 軸から 5 単位 (下) 離れた位置になります。
異なる象限の三角関数の値
さまざまな価値観 三角関数 さまざまな象限での結果は、以下に追加された表を検討することで学習できます。
| 四分円 | それなし | コス | それで | コセカント | 割線 | コタンジェント |
|---|---|---|---|---|---|---|
| 第 1 象限 | + | + | + | + | + | + |
| 第2象限 | + | – | + | + | – | – |
| 第3象限 | – | – | – | – | – Q1はいつ終わりますか | + |
| 第4象限 | – | – | – | – | + | – |
第 1 象限では、すべての三角比が正になります。第 2 象限では、サインとコセカントは正 (+) ですが、コサインとセカントは負 (-) です。第 3 象限では、タンジェントとコタンジェントは正 (+) ですが、コサインとセカントは負 (-) です。第 4 象限では、サインとコセカントは負 (-) ですが、コサインとセカントは正 (+) です。
続きを読む、
- 座標ジオメトリ
- 平行線
- 距離の公式
クワドラントの解決例
例 1: 点 A (3, -4) をプロットし、その象限を特定します。
解決:
点 A は座標 (3, -4) にあります。 x 座標は正 (3)、y 座標は負 (-4) であるため、点 A は象限 IV にあります。
例 2: 点 P (-5, 2) をプロットし、その象限を決定します
解決:
点 P の座標は (-5, 2) です。象限を決定するには、x 座標と y 座標の符号を調べます。
X 座標は -5 で、原点の左側の位置を示します。
Y 座標は 2 で、原点より上の位置を示します。
したがって、x 座標が負で y 座標が正であるため、点 P は象限 II に位置します。
点 P (-5, 2) は、デカルト平面の象限 II に位置します。
象限に関する練習問題
問題 1: 点 (1, -1) をプロットし、その象限を特定します。
問題 2: X 軸上の 3 つの点を見つけて、その象限を決定します。
Javaがnullです
問題 3: 点が座標 (0, -3) の y 軸上にある場合、その点はどの象限にありますか?
問題 4: 点 Q (2, 2)、R (-2, -2)、および S (0, 0) を見つけて、共線性を確認します。
問題 5: 点 (-4、-3) をプロットし、それがどの象限に位置するかを説明します。
クワドラントに関するよくある質問
1. 数学における象限とは何ですか?
数学では、四分円は 2 本の垂直線または軸の交差によって作成される 4 つのセクションのうちの 1 つです。これらの軸は通常、デカルト座標系で x 軸および y 軸としてラベル付けされます。
2. 2 つの軸の交点は何と呼ばれますか?
デカルト座標系の 2 つの軸の交点は原点と呼ばれます。これは、x 軸と y 軸が交わる点で表され、通常は (0,0) と表されます。
3. 4象限とは何ですか?
4 つの象限は、デカルト座標平面を 4 つの等しい部分に分割することによって形成されるセクションです。それらは、第 1 象限 (Q1)、第 2 象限 (Q2)、第 3 象限 (Q3)、および第 4 象限 (Q4) としてラベル付けされます。
4. どの象限がポジティブですか?
デカルト座標系の正の象限は、第 1 象限 (Q1) です。この象限では、x 座標と y 座標は両方とも正です。
5. グラフにおける象限の使用法は何ですか?
グラフの象限は、座標に基づいて点を整理し、位置を特定する体系的な方法を提供します。これらは、変数間の関係を視覚化し、データセット内のパターンを分析するのに役立ち、グラフ表現の解釈を容易にします。
6. 両方の座標が正の値を持つ象限はどれですか?
第 1 象限 (Q1) は、点の x 座標と y 座標が両方とも正である象限です。これは、両方の正の値を持つ唯一の象限です。
7. 円の 4 つの象限とは何ですか?
象限の概念は円には直接適用できません。代わりに、円は度単位で測定される角度に分割されます。ただし、円形セクターに言及する場合は、異なる角度領域に対応する、第 1 セクター、第 2 セクター、第 3 セクター、第 4 セクターなどの用語を使用する場合があります。
