量子数 化学では、原子内の電子の軌道と動きを表す一連の数値です。特定の原子内のすべての電子の量子数を合計すると、次の条件を満たさなければなりません。 シュレーディンガー方程式 。
量子数は、原子内の電子の位置とエネルギーを記述するために使用される一連の数値です。量子数には、主数、方位数、磁気数、スピン数の 4 種類があります。量子数は、量子システムの保存された量の値を表します。
この記事では、すべての量子数について詳しく学びましょう。
目次
量子数とは何ですか?
量子数は、量子アプローチにおける定数値のセットです。量子数または 電子量子数 水素原子のシュレーディンガー波動方程式の解を与える数値で電子を記述する。これらの数値は、一連の数値を通じて原子内の電子の位置、エネルギー、および方向を定義できます。
Javaが例外をスローする
による パウリの排除原則 、原子内の 2 つの電子が同じ量子数セットを持つことはできません。半整数または整数値は、各量子数を特徴付けるために使用されます。主量子数、方位角量子数、磁気量子数は、それぞれ原子のサイズ、形状、向きに関係します。
4 つの量子数を使用すると、原子内の特定の電子の特性をすべて完全に記述することができます。これらは:
- 主量子数
- 軌道角運動量子数 (または方位角量子数)。
- 磁気量子数
- 電子スピン量子数
量子数の種類
4 つの量子数は、原子内の電子のすべての特性を完全に記述するために使用されます。これらの量子数は次のとおりです。
- 主量子数 (n)
- 方位量子数 (l)
- 磁気量子数 (m私)
- 電子スピン量子数 (s)
主量子数 (n)
記号「n」は主量子数を表します。それらは原子の一次電子殻を表します。これは原子核と電子の間の最も可能性の高い距離を表すため、主量子数の値が大きいほど、電子と原子核の間の距離が大きいことを意味します (つまり、原子サイズが大きいことを意味します)。
- 主量子数の値は、1 以上の正の値を持つ任意の整数です。値 n=1 は、原子の最も内側の電子殻を示し、電子の最低エネルギー状態 (または基底状態) に対応します。
- その結果、原子は負の値を持つことができない、または主シェルの値が存在しないため、主量子数 n は負の値を持つこともゼロに等しくなることもありません。
- 電子にエネルギーが注入されると (励起状態)、電子は 1 つの主殻からより高い殻にジャンプし、n の値が増加します。
- 同様に、電子はエネルギーを失うと下層の殻に戻り、n の値が低下します。吸収とは、電子の n 値の増加を指し、電子によって吸収される光子またはエネルギーが強調されます。
- 同様に、電子の n 値の減少は放出と呼ばれ、ここで電子はエネルギーを放出します。
方位角量子数 (l) – 軌道角運動量子数
方位量子数 (または軌道角運動量) は軌道の形状を表します。これは文字「l」で表され、その値は軌道内の角度ノードの総数に等しくなります。
- 方位量子数の値は、形状が異なる s、p、d、または f サブシェルのいずれかを表すことができます。
- この値は、主量子数の値によって決定 (および制限) されます。つまり、方位角量子数の範囲は 0 から (n-1) です。
- たとえば、n = 3 の場合、方位量子数は 0、1、2 の 3 つの値を持つことができます。
- l をゼロに設定すると、結果のサブシェルは「s」サブシェルになります。
- l=1 および l=2 の場合、結果のサブシェルはそれぞれ「p」サブシェルと「d」サブシェルになります。
- その結果、n=3 の場合、存在できるサブシェルは 3s、3p、および 3d の 3 つになります。 n = 5 の別のケースでは、l の可能な値は 0、1、2、3、および 4 です。l = 3 の場合、アトムには 3 つの角度ノードが含まれます。
磁気量子数 (m私)
磁気量子数は、サブシェル内の軌道の総数とその方向を決定します。それは記号「m」で表されます。私この数値は、特定の軸に沿った軌道の角運動量の投影を表します。
- 磁気量子数は、方位角 (または軌道角運動量) 量子数によって決まります。
- l の値が指定された場合、m の値は私-l から +l の間に収まります。その結果、n の値に間接的に依存します。
- たとえば、原子内の n = 4 および l = 3 の場合、磁気量子数は -3、-2、-1、0、+1、+2、および +3 になります。特定のサブシェル内の軌道の総数は、軌道の「l」値によって決まります。
- 式(2l + 1)を使用して計算されます。たとえば、「3d」サブシェル (n=3、l=2) には 5 つの軌道 (2*2 + 1) があります。各軌道は 2 つの電子を保持できます。その結果、3d サブシェルは合計 10 個の電子を収容できるようになります。
電子スピン量子数 (s)
電子のスピン量子数はn、l、mに依存しません。私価値観。この数値の値は記号 m で示されます。s, 電子が回転する方向を示します。
- 彼らs値は電子が回転する方向を示します。電子のスピン量子数は +1/2 から -1/2 までの値をとることができます。
- m の正の値sは電子の上向きスピンを示し、スピンアップとも呼ばれます。
- もしmならsが負の場合、問題の電子は下向きスピンまたはスピンダウンを持っていると言われます。
- 電子のスピン量子数の値によって、当該原子が磁場を生成できるかどうかが決まります。 mの値s±1/2 に一般化できます。
量子数の重要性
量子数は、原子の電子配置とその電子が最も存在する可能性が高い場所を推定するために使用できるため、重要です。原子の原子半径とイオン化エネルギー、その他の特性も量子数によって決まります。
各量子数には、次の表で説明する独自の意味があります。
| 番号 | シンボル | 可能な値 | 意義 |
|---|---|---|---|
| 主量子数 | n | 1、2、3、4、5、…。 | 原子の電子レベルを表します。 |
| 方位量子数 | 私 | 0、1、2、3、…。 (n-1) | 電子雲の形状を表します。 |
| 磁気量子数 | メートル私 | -l、….、-1、0、1、….、l | 電子雲の向きを説明します。 |
| スピン量子数 | s | +1/2、-1/2 | それは電子が持つことができるスピンを示しています。 numpy ドット積 |
原子軌道
ご存知のとおり、電子は波のように振る舞い、原子内の電子の位置は、原子の特定のエネルギー準位でシュレディンガー波動方程式を解くことにより、量子力学の波動理論を利用して簡単に定義できます。
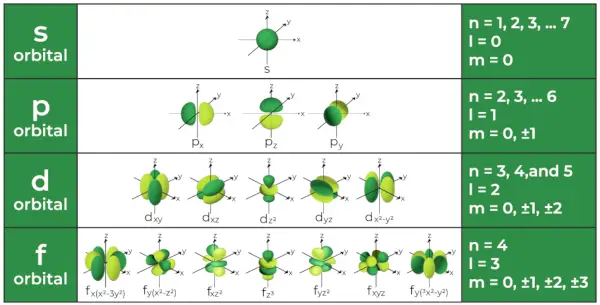
原子内の電子の位置を定義するこれらの波動関数は、原子軌道と呼ばれます。これらの軌道は、電子が見つかる確率が最も高い場所です。原子の中には4種類の軌道がある
- s – 軌道
- p – 軌道
- d – 軌道
- f – 軌道
原子軌道は、電子を見つける確率が最も高い原子内部の物理空間としても定義されます。
続きを読む:
- 要素の電子構成
- アトムの軌道の充填
- 原子軌道の形状
電子の位置と経路に関連するその他の法則
化学における他の 3 つの規則と原則は、原子内の電子の位置、経路、軌道、エネルギー レベルを理解するのに役立ちます。これらについては、後続のサブセクションで説明します。
構造原理
アウフバウの法則とも呼ばれるアウフバウの原理は、電子は高エネルギーの原子軌道よりも先に低エネルギーの原子軌道に入るというものです。アウフバウとはドイツ語で「築く」という意味です。
NCERT の構造原理の定義
原子の基底状態では、軌道はエネルギーの増加順に満たされます。
の 建設原理 電子が原子やイオン内でどのように配置されるかを理解するのに役立ちます。たとえば、1 秒のサブシェルは 2 秒のサブシェルよりも前にいっぱいになります。
電子が軌道を満たす順序は次のとおりです: 1s、2s、2p、3s、3p、4s、3d、4p、5s、4d、5p、6s、4f、5d、6p、7s、5f、6d、7p、など。この充填パターンはすべての原子に適用されます。
のために 例 、アウフバウの原理を使用すると、 硫黄の電子配置 と書かれています [S] = 1s2 2s2 2p6 3s2 3p4。
フントの最大多重度の法則
フントの法則によれば、サブレベルの各軌道は、2 番目の電子を取得する前に 1 つの電子を取得します。そして、これらの単一占有軌道内の電子はすべて同じスピンを持っています。
NCERT によるフンドの法則の定義
同じサブシェル (p、d、または f) に属する軌道内の電子の対形成は、そのサブシェルに属する各軌道がそれぞれ 1 つの電子を獲得するまで、つまり単独で占有されるまで起こりません。
フントの法則は最大多重度の法則とも呼ばれ、原子が複数の不対電子を持つことになります。これらの不対電子はさまざまな方向に回転することができ、さまざまな方向に磁気モーメントを生成します。
フントの法則は、不対電子を持つ特定の分子に適用されます。
パウリの排除原則
パウリの排他原理は、半整数スピンを持つ 2 つの同一の粒子が系内で同じ量子状態になることはできない、というものです。
NCERT によるパウリ除外原則の定義
原子内の 2 つの電子が同じ 4 つの量子数のセットを持つことはできません。
または
同じ軌道に存在できる電子は 2 つだけであり、これらの電子は逆のスピンを持っていなければなりません。
化学では、 パウリの排除原則 同じ原子内では、2 つの電子が 4 つの量子数すべてを同一にすることはできないことがわかります。これは、最大でも 2 つの電子が同じ軌道を占有することができ、それらは逆のスピンを持たなければならないことを意味します。
パウリの排他原理により、シェルまたはサブシェル内に存在できる電子の数に制限が設定されます。
セグメンテーションフォールトコアダンプ
量子数に関する解決された質問
質問 1: ルビジウムの最後の電子の 4 つの量子数をすべて見つけてください。
解決:
ルビジウムの原子番号は Z = 37 です。
ルビジウムの電子配置、
1秒22秒22P63秒23P63D104秒24P65秒1
最終殻電子の価数は5s1
したがって、
主量子数、n = 5、
方位量子数、l = 0、
磁気量子数、m私= 0、
スピン量子数、s = +1/2
質問 2: l = 2 の場合の磁気量子数の可能な値を述べてください。
解決:
それを考慮すると、方位量子数 l = 2
私達はことを知っています、
メートル私= – l ~ + l
したがって、
メートル私= -2 ~ +2
つまり
メートル2= -2、-1、0、+1、+2
質問 3: ナトリウムの最後の電子の 4 つの量子数をすべて見つけてください。
解決:
ナトリウムの原子番号は Z = 11 です。
ルビジウムの電子配置、
1秒22秒22P63秒1
価電子殻の最後の電子は 3 秒です1
したがって、
主量子数、n = 3、
方位量子数、l = 0、
磁気量子数、m私= 0、
jリストスピン量子数、s = +1/2
質問 4: l = 3 の場合の磁気量子数の取り得る値を述べてください。
解決:
それを考慮すると、方位量子数、l = 3
私達はことを知っています、
l = 3の場合、
メートル私= – 3 ~ + 3
つまり
m = -3 、 -2、-1、0、+1、+2 +3
量子数 MCQ の練習問題
量子数の実践についてさらに詳しく知るには 定量的な数値に関する MCQ
量子数に関するよくある質問
量子数を定義する。
原子内の電子の数の位置とエネルギーを定義するために使用される一連の数値は、量子数と呼ばれます。
量子数はいくつありますか?
4 つの量子数は次のとおりです。
- 主量子数 (n)
- 方位量子数 (l)
- 磁気量子数 (m私)
- 電子スピン量子数 (s)
軌道の形状を指定する量子数はどれですか?
方位量子数 (l) は角量子数とも呼ばれ、軌道の形状を定義します。
軌道の向きを決定する量子数はどれですか?
磁気量子数 (m私) は、3 次元空間における軌道の方向を表すために使用されます。
軌道を指定するには量子数はいくつ必要ですか?
原子の軌道を指定するには、次の 3 つの量子数が必要です。
- 主量子数 (n)
- 方位量子数 (l)
- 磁気量子数 (m私)
電子のエネルギーを決定する量子数はどれですか?
電子のエネルギーは、電子の主量子数(n)と方位量子数(l)を使用することで簡単に求めることができます。
量子エネルギーとは何ですか?
量子粒子 (つまり、非常に小さな粒子) のエネルギーは、量子エネルギーと呼ばれます。量子エネルギーを測定する 1 つの方法は、光エネルギーや他の電磁波のエネルギーを測定する最小単位である光子を使用することです。
電子のスピンとは何ですか?
電子スピンは電子の量子的性質です。角運動量を持った形です。指導手法として、インストラクターは電子のスピンを 24 時間ごとに自転する惑星と比較します。スピンアップは、電子がその軸上で時計回りに回転するときに発生します。スピンダウンは電子が反時計回りに回転するときに発生します。
建設原理とは何ですか?
構造原理 電子が原子内の原子軌道をどのように埋めるかを説明する化学の概念です。この原理によれば、電子は、より高いエネルギーの軌道に移動する前に、利用可能な最も低いエネルギーの軌道を占有します。
フントの法則クラス 11 とは何ですか?
フントの法則は、クラス 11 化学でよく議論されるもので、電子はペアになる前に同じエネルギー準位の軌道 (サブシェル) を単独で占有すると述べています。さらに、単一占有軌道内の電子は平行スピンを持ちます。
SPDFのフルフォームとは何ですか?
SPDF は、原子内の 4 つのサブレベルまたは軌道、s、p、d、f を表します。これらの文字は、電子が存在する可能性が高い原子軌道のさまざまな形状と方向を表しています。
- S:シャープ
- Q:メイン
- D: 拡散
- F: 基本的な
なぜ量子は量子と呼ばれるのでしょうか?
量子という用語は、ラテン語の意味に由来しています。 いくら または 量 。物理学では、エネルギーや運動量などの特定の物理量が量子論に従って量子化される、離散的で分割不可能な単位を指します。これらの個別の単位は、原子および亜原子レベルで粒子の挙動を理解するための基礎となります。したがって、量子物理学の分野は量子化の概念にちなんで名付けられました。
