logo

TechCodeview

最小スパニング ツリーの逆削除アルゴリズム

GfG Practice で試してみる 最小スパニング ツリーの逆削除アルゴリズム' title= #practiceLinkDiv { 表示: なし !重要; }

逆削除アルゴリズムは次のものと密接に関連しています クラスカルのアルゴリズム 。 Kruskal のアルゴリズムでは、重みの昇順でエッジを並べ替えます。ソート後、昇順でエッジを 1 つずつ選択します。スパニング ツリーに V-1 エッジ (V = 頂点の数) が存在するまで、これをスパニング ツリーに含めることによってサイクルが形成されない場合は、現在選択されているエッジを含めます。

逆削除アルゴリズムでは、すべてのエッジを次のようにソートします。 減少する 重さの順番。ソート後、降順でエッジを 1 つずつ選択します。私たちは 現在のエッジを除外すると現在のグラフが切断される場合は、現在選択されているエッジを含めます 。主なアイデアは、エッジの削除がグラフの切断につながらない場合はエッジを削除することです。

typescript の foreach ループ

アルゴリズム:



  1. グラフのすべてのエッジをエッジの重みの非増加順に並べ替えます。
  2. MST を元のグラフとして初期化し、手順 3 を使用して余分なエッジを削除します。
  3. 残りのエッジから最も重みの高いエッジを選択し、 エッジを削除するとグラフが切断されるかどうかを確認します 。
     切断された場合、エッジは削除されません。
    それ以外の場合は、エッジを削除して続行します。 

図：  

次の例で理解してみましょう。

逆削除2


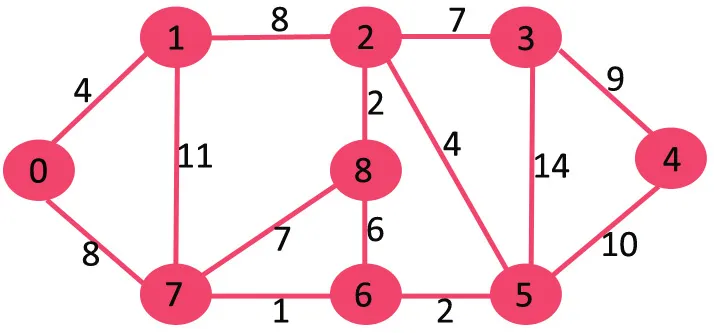
重み14の最も高い重みの辺を削除するとグラフが切れなくなるので削除します。 
 

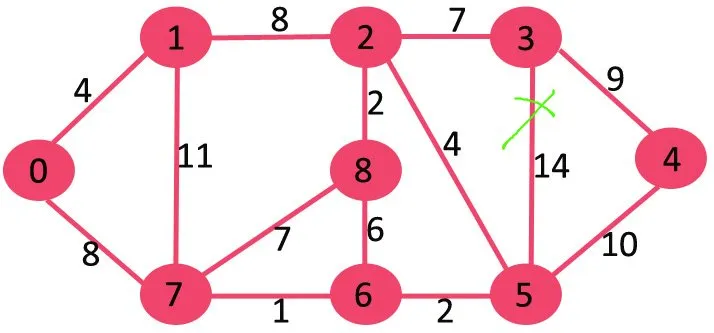
逆削除3' title=


次に、11 を削除します。削除してもグラフは切断されません。 
 

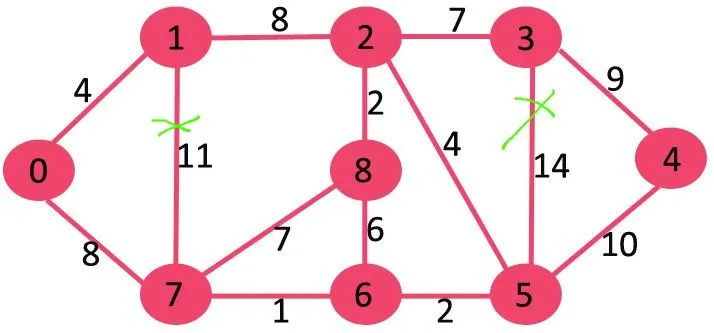
逆削除4' title=


次に、10 を削除します。削除してもグラフは切断されません。 
 

逆削除5' title=


次は9です。9を削除すると切断の原因となるため削除できません。 
 

' title=


このまま続行すると、最終的な MST に次のエッジが残ります。 

Edges in MST  
(3 4)   
(0 7)   
(2 3)   
(2 5)   
(0 1)   
(5 6)   
(2 8)   
(6 7)

注記 ： 同じ重みのエッジの場合は、同じ重みのエッジの任意のエッジを選択できます。

推奨される実践方法 最小スパニング ツリーの逆削除アルゴリズム 試してみてください!

実装：

C++ 
// C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #include   using namespace std; // Creating shortcut for an integer pair typedef pair<int int> iPair; // Graph class represents a directed graph // using adjacency list representation class Graph {  int V; // No. of vertices  list<int> *adj;  vector< pair<int iPair> > edges;  void DFS(int v bool visited[]); public:  Graph(int V); // Constructor  // function to add an edge to graph  void addEdge(int u int v int w);  // Returns true if graph is connected  bool isConnected();  void reverseDeleteMST(); }; Graph::Graph(int V) {  this->V = V;  adj = new list<int>[V]; } void Graph::addEdge(int u int v int w) {  adj[u].push_back(v); // Add w to v’s list.  adj[v].push_back(u); // Add w to v’s list.  edges.push_back({w {u v}}); } void Graph::DFS(int v bool visited[]) {  // Mark the current node as visited and print it  visited[v] = true;  // Recur for all the vertices adjacent to  // this vertex  list<int>::iterator i;  for (i = adj[v].begin(); i != adj[v].end(); ++i)  if (!visited[*i])  DFS(*i visited); } // Returns true if given graph is connected else false bool Graph::isConnected() {  bool visited[V];  memset(visited false sizeof(visited));  // Find all reachable vertices from first vertex  DFS(0 visited);  // If set of reachable vertices includes all  // return true.  for (int i=1; i<V; i++)  if (visited[i] == false)  return false;  return true; } // This function assumes that edge (u v) // exists in graph or not void Graph::reverseDeleteMST() {  // Sort edges in increasing order on basis of cost  sort(edges.begin() edges.end());  int mst_wt = 0; // Initialize weight of MST  cout << 'Edges in MSTn';  // Iterate through all sorted edges in  // decreasing order of weights  for (int i=edges.size()-1; i>=0; i--)  {  int u = edges[i].second.first;  int v = edges[i].second.second;  // Remove edge from undirected graph  adj[u].remove(v);  adj[v].remove(u);  // Adding the edge back if removing it  // causes disconnection. In this case this   // edge becomes part of MST.  if (isConnected() == false)  {  adj[u].push_back(v);  adj[v].push_back(u);  // This edge is part of MST  cout << '(' << u << ' ' << v << ') n';  mst_wt += edges[i].first;  }  }  cout << 'Total weight of MST is ' << mst_wt; } // Driver code int main() {  // create the graph given in above figure  int V = 9;  Graph g(V);  // making above shown graph  g.addEdge(0 1 4);  g.addEdge(0 7 8);  g.addEdge(1 2 8);  g.addEdge(1 7 11);  g.addEdge(2 3 7);  g.addEdge(2 8 2);  g.addEdge(2 5 4);  g.addEdge(3 4 9);  g.addEdge(3 5 14);  g.addEdge(4 5 10);  g.addEdge(5 6 2);  g.addEdge(6 7 1);  g.addEdge(6 8 6);  g.addEdge(7 8 7);  g.reverseDeleteMST();  return 0; }
Java 
// Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.*; // class to represent an edge class Edge implements Comparable<Edge> {  int u v w;  Edge(int u int v int w)  {  this.u = u;  this.w = w;  this.v = v;  }  public int compareTo(Edge other)  {  return (this.w - other.w);  } } // Class to represent a graph using adjacency list // representation public class GFG {  private int V; // No. of vertices  private List<Integer>[] adj;  private List<Edge> edges;  @SuppressWarnings({ 'unchecked' 'deprecated' })  public GFG(int v) // Constructor  {  V = v;  adj = new ArrayList[v];  for (int i = 0; i < v; i++)  adj[i] = new ArrayList<Integer>();  edges = new ArrayList<Edge>();  }  // function to Add an edge  public void AddEdge(int u int v int w)  {  adj[u].add(v); // Add w to v’s list.  adj[v].add(u); // Add w to v’s list.  edges.add(new Edge(u v w));  }  // function to perform dfs  private void DFS(int v boolean[] visited)  {  // Mark the current node as visited and print it  visited[v] = true;  // Recur for all the vertices adjacent to  // this vertex  for (int i : adj[v]) {  if (!visited[i])  DFS(i visited);  }  }  // Returns true if given graph is connected else false  private boolean IsConnected()  {  boolean[] visited = new boolean[V];  // Find all reachable vertices from first vertex  DFS(0 visited);  // If set of reachable vertices includes all  // return true.  for (int i = 1; i < V; i++) {  if (visited[i] == false)  return false;  }  return true;  }  // This function assumes that edge (u v)  // exists in graph or not  public void ReverseDeleteMST()  {  // Sort edges in increasing order on basis of cost  Collections.sort(edges);  int mst_wt = 0; // Initialize weight of MST  System.out.println('Edges in MST');  // Iterate through all sorted edges in  // decreasing order of weights  for (int i = edges.size() - 1; i >= 0; i--) {  int u = edges.get(i).u;  int v = edges.get(i).v;  // Remove edge from undirected graph  adj[u].remove(adj[u].indexOf(v));  adj[v].remove(adj[v].indexOf(u));  // Adding the edge back if removing it  // causes disconnection. In this case this  // edge becomes part of MST.  if (IsConnected() == false) {  adj[u].add(v);  adj[v].add(u);  // This edge is part of MST  System.out.println('(' + u + ' ' + v  + ')');  mst_wt += edges.get(i).w;  }  }  System.out.println('Total weight of MST is '  + mst_wt);  }  // Driver code  public static void main(String[] args)  {  // create the graph given in above figure  int V = 9;  GFG g = new GFG(V);  // making above shown graph  g.AddEdge(0 1 4);  g.AddEdge(0 7 8);  g.AddEdge(1 2 8);  g.AddEdge(1 7 11);  g.AddEdge(2 3 7);  g.AddEdge(2 8 2);  g.AddEdge(2 5 4);  g.AddEdge(3 4 9);  g.AddEdge(3 5 14);  g.AddEdge(4 5 10);  g.AddEdge(5 6 2);  g.AddEdge(6 7 1);  g.AddEdge(6 8 6);  g.AddEdge(7 8 7);  g.ReverseDeleteMST();  } } // This code is contributed by Prithi_Dey
Python3 
# Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph: def __init__(self v): # No. of vertices self.v = v self.adj = [0] * v self.edges = [] for i in range(v): self.adj[i] = [] # function to add an edge to graph def addEdge(self u: int v: int w: int): self.adj[u].append(v) # Add w to v’s list. self.adj[v].append(u) # Add w to v’s list. self.edges.append((w (u v))) def dfs(self v: int visited: list): # Mark the current node as visited and print it visited[v] = True # Recur for all the vertices adjacent to # this vertex for i in self.adj[v]: if not visited[i]: self.dfs(i visited) # Returns true if graph is connected # Returns true if given graph is connected else false def connected(self): visited = [False] * self.v # Find all reachable vertices from first vertex self.dfs(0 visited) # If set of reachable vertices includes all # return true. for i in range(1 self.v): if not visited[i]: return False return True # This function assumes that edge (u v) # exists in graph or not def reverseDeleteMST(self): # Sort edges in increasing order on basis of cost self.edges.sort(key = lambda a: a[0]) mst_wt = 0 # Initialize weight of MST print('Edges in MST') # Iterate through all sorted edges in # decreasing order of weights for i in range(len(self.edges) - 1 -1 -1): u = self.edges[i][1][0] v = self.edges[i][1][1] # Remove edge from undirected graph self.adj[u].remove(v) self.adj[v].remove(u) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self.connected() == False: self.adj[u].append(v) self.adj[v].append(u) # This edge is part of MST print('( %d %d )' % (u v)) mst_wt += self.edges[i][0] print('Total weight of MST is' mst_wt) # Driver Code if __name__ == '__main__': # create the graph given in above figure V = 9 g = Graph(V) # making above shown graph g.addEdge(0 1 4) g.addEdge(0 7 8) g.addEdge(1 2 8) g.addEdge(1 7 11) g.addEdge(2 3 7) g.addEdge(2 8 2) g.addEdge(2 5 4) g.addEdge(3 4 9) g.addEdge(3 5 14) g.addEdge(4 5 10) g.addEdge(5 6 2) g.addEdge(6 7 1) g.addEdge(6 8 6) g.addEdge(7 8 7) g.reverseDeleteMST() # This code is contributed by # sanjeev2552
C# 
// C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System; using System.Collections.Generic; // class to represent an edge public class Edge : IComparable<Edge> {  public int u v w;  public Edge(int u int v int w)  {  this.u = u;  this.v = v;  this.w = w;  }  public int CompareTo(Edge other)  {  return this.w.CompareTo(other.w);  } } // Graph class represents a directed graph // using adjacency list representation public class Graph {  private int V; // No. of vertices  private List<int>[] adj;  private List<Edge> edges;  public Graph(int v) // Constructor  {  V = v;  adj = new List<int>[ v ];  for (int i = 0; i < v; i++)  adj[i] = new List<int>();  edges = new List<Edge>();  }  // function to Add an edge  public void AddEdge(int u int v int w)  {  adj[u].Add(v); // Add w to v’s list.  adj[v].Add(u); // Add w to v’s list.  edges.Add(new Edge(u v w));  }  // function to perform dfs  private void DFS(int v bool[] visited)  {  // Mark the current node as visited and print it  visited[v] = true;  // Recur for all the vertices adjacent to  // this vertex  foreach(int i in adj[v])  {  if (!visited[i])  DFS(i visited);  }  }  // Returns true if given graph is connected else false  private bool IsConnected()  {  bool[] visited = new bool[V];  // Find all reachable vertices from first vertex  DFS(0 visited);  // If set of reachable vertices includes all  // return true.  for (int i = 1; i < V; i++) {  if (visited[i] == false)  return false;  }  return true;  }  // This function assumes that edge (u v)  // exists in graph or not  public void ReverseDeleteMST()  {  // Sort edges in increasing order on basis of cost  edges.Sort();  int mst_wt = 0; // Initialize weight of MST  Console.WriteLine('Edges in MST');  // Iterate through all sorted edges in  // decreasing order of weights  for (int i = edges.Count - 1; i >= 0; i--) {  int u = edges[i].u;  int v = edges[i].v;  // Remove edge from undirected graph  adj[u].Remove(v);  adj[v].Remove(u);  // Adding the edge back if removing it  // causes disconnection. In this case this  // edge becomes part of MST.  if (IsConnected() == false) {  adj[u].Add(v);  adj[v].Add(u);  // This edge is part of MST  Console.WriteLine('({0} {1})' u v);  mst_wt += edges[i].w;  }  }  Console.WriteLine('Total weight of MST is {0}'  mst_wt);  } } class GFG {  // Driver code  static void Main(string[] args)  {  // create the graph given in above figure  int V = 9;  Graph g = new Graph(V);  // making above shown graph  g.AddEdge(0 1 4);  g.AddEdge(0 7 8);  g.AddEdge(1 2 8);  g.AddEdge(1 7 11);  g.AddEdge(2 3 7);  g.AddEdge(2 8 2);  g.AddEdge(2 5 4);  g.AddEdge(3 4 9);  g.AddEdge(3 5 14);  g.AddEdge(4 5 10);  g.AddEdge(5 6 2);  g.AddEdge(6 7 1);  g.AddEdge(6 8 6);  g.AddEdge(7 8 7);  g.ReverseDeleteMST();  } } // This code is contributed by cavi4762
JavaScript 
// Javascript program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm // Graph class represents a directed graph // using adjacency list representation class Graph {  // Constructor  constructor(V) {  this.V = V;  this.adj = [];  this.edges = [];  for (let i = 0; i < V; i++) {  this.adj[i] = [];  }  }    // function to add an edge to graph  addEdge(u v w) {  this.adj[u].push(v);// Add w to v’s list.  this.adj[v].push(u);// Add w to v’s list.  this.edges.push([w [u v]]);  }  DFS(v visited) {  // Mark the current node as visited and print it  visited[v] = true;  for (const i of this.adj[v]) {  if (!visited[i]) {  this.DFS(i visited);  }  }  }  // Returns true if given graph is connected else false  isConnected() {  const visited = [];  for (let i = 0; i < this.V; i++) {  visited[i] = false;  }    // Find all reachable vertices from first vertex  this.DFS(0 visited);    // If set of reachable vertices includes all  // return true.  for (let i = 1; i < this.V; i++) {  if (!visited[i]) {  return false;  }  }  return true;  }  // This function assumes that edge (u v)  // exists in graph or not  reverseDeleteMST() {    // Sort edges in increasing order on basis of cost  this.edges.sort((a b) => a[0] - b[0]);    let mstWt = 0;// Initialize weight of MST    console.log('Edges in MST');    // Iterate through all sorted edges in  // decreasing order of weights  for (let i = this.edges.length - 1; i >= 0; i--) {  const [u v] = this.edges[i][1];    // Remove edge from undirected graph  this.adj[u] = this.adj[u].filter(x => x !== v);  this.adj[v] = this.adj[v].filter(x => x !== u);    // Adding the edge back if removing it  // causes disconnection. In this case this   // edge becomes part of MST.  if (!this.isConnected()) {  this.adj[u].push(v);  this.adj[v].push(u);    // This edge is part of MST  console.log(`(${u} ${v})`);  mstWt += this.edges[i][0];  }  }  console.log(`Total weight of MST is ${mstWt}`);  } } // Driver code function main() {  // create the graph given in above figure  var V = 9;  var g = new Graph(V);  // making above shown graph  g.addEdge(0 1 4);  g.addEdge(0 7 8);  g.addEdge(1 2 8);  g.addEdge(1 7 11);  g.addEdge(2 3 7);  g.addEdge(2 8 2);  g.addEdge(2 5 4);  g.addEdge(3 4 9);  g.addEdge(3 5 14);  g.addEdge(4 5 10);  g.addEdge(5 6 2);  g.addEdge(6 7 1);  g.addEdge(6 8 6);  g.addEdge(7 8 7);  g.reverseDeleteMST(); } main();

出力 
Edges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37

時間計算量: O((E*(V+E)) + E log E) ここで、E はエッジの数です。

空間複雑さ: O(V+E) ここで、V は頂点の数、E はエッジの数です。隣接リストを使用してグラフを保存しているため、O(V+E) に比例するスペースが必要です。

iCloud写真にアクセスする方法

注: 

  1. 上記の実装は、逆削除アルゴリズムの単純/素朴な実装であり、O(E log V (log log V) に最適化できます。3） [ソース ： 一週間 ]。しかし、この最適化された時間計算量は依然として プリム そして クラスカル MST のアルゴリズム。
  2. 上記の実装では、元のグラフが変更されます。元のグラフを保持する必要がある場合は、グラフのコピーを作成できます。

 

クイズの作成